Быстрое преобразование Фурье (БПФ)

Дискретное преобразование Фурье X(k) конечной последовательности

X(nT), n=0, 1, 2, …, N-1 определяется согласно (2.19), (2.20):

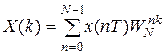, k=0, 1, 2, …, N-1; (2.21)

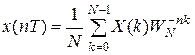, n=0, 1, 2, …, N-1, (2.22)

где ,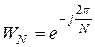

причем W_N является периодической последовательностью с периодом N, так как 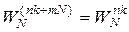, m=0, ±1, ±2, …. Непосредственное вычисление ДПФ (2.21) при комплексных значениях x(nT) требует для каждого значения k (N-1) умножений и (N-1) сложений комплексных чисел или 4(N-1) умножений и (2N-2) сложений действительных чисел, а для всех N значений k=0, 1, 2, …, N-1 требуется примерно N² умножений и N² сложений комплексных чисел. Таким образом, для больших значений N (порядка нескольких сотен или тысяч) прямое вычисление ДПФ требует выполнения весьма большого числа арифметических операций умножения и сложения, что затрудняет реализацию вычисления в реальном масштабе времени процессов и спектров.

Быстрым преобразованием Фурье называют набор алгоритмов, реализация которых приводит к существенному уменьшению вычислительной сложности ДПФ. Исходная идея алгоритмов состоит в том, что N-точечная последовательность разбивается на две более короткие, например на две (N/2)-точечных последовательности, вычисляются ДПФ для этих более коротких последовательностей и из этих ДПФ конструируется ДПФ исходной последовательности. Для двух (N/2)-точечных последовательностей требуется примерно (N/2)²*2=N²/2 умножений комплексных чисел, т.е. число умножений ( а так же сложений) уменьшается примерно в 2 раза. Аналогично вместо вычисления ДПФ (N/2)- точечной последовательности можно вычислить ДПФ для двух (N/4)-точечных последовательностей и таким образом вновь сократить требуемое количество операций умножения и сложения. Если N=2ⁿ, n>0 и целое, то процесс уменьшения размера ДПФ может быть продолжен до тех пор, пока не останутся только 2-точечные ДПФ. При этом общее число этапов вычисления ДПФ будет равно n=log₂N раз, а число требуемых операций для вычисления N-точечной ДПФ будет порядка Nn, т.е. уменьшается примерно в 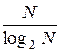раз. Так при N=1000 для прямого вычисления ДПФ согласно (2.21) требуется примерно N²=10⁶ операций комплексных умножений и сложений, а при использовании алгоритмов БПФ таких операций требуется всего порядка 10⁴, т.е. объем вычислений сокращается примерно на два порядка.

Существуют различные алгоритмы БПФ, например, широко распространены алгоритм с прореживанием по времени, в котором требуется перестановка отсчетов входной последовательности x(nT) и алгоритм с прореживанием по частоте, в котором требуется перестановка отсчетов выходной последовательности X(k). В обоих алгоритмах БПФ требуется примерно Nlog₂N операций (комплексных умножений) и оба алгоритма могут быть реализованы по способу с замещением, используя только один массив ячеек памяти.