Оптимальная обработка сильно коррелированных портретов

Обратимся теперь к случаю сильно коррелированных портретов. Многомерная плотность вероятности совокупности комплексных амплитуд η_n принятого сигнала, относящихся к N элементам пространства распознавания в отсутствии портрета (η_n = ξ_no) при некоррелированном фоне 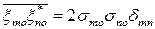, определяется выражением:

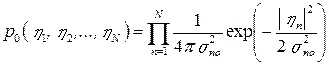
или, в более общем виде, следующим выражением:

,

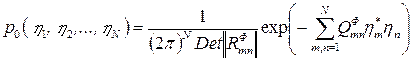где 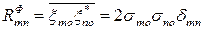- элементы корреляционной матрицы фона; Q^Ф_mn - элементы матрицы, обратной матрице ║R^Ф_mn║, Det║R^Ф_mn║ - определитель матрицы ║R^Ф_mn║.

Многомерная плотность вероятности совокупных комплексных амплитуд η_n = ξ_nк + ξ_no при наличии коррелированного портрета К-го класса определяется аналогичным выражением:

,

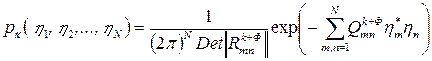где 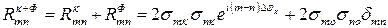- элементы корреляционной матрицы К-го портрета и фона, ∆φ_к – межэлементный набег фазы К-го портрета, Q^к+Ф_mn – элементы матрицы, обратной матрице║R^к+Ф_mn║,

.

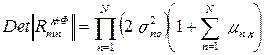При этом логарифм отношения правдоподобия, определяющий алгоритм оптимальной обработки коррелированного портрета К-го класса представляется в следующем виде:

,

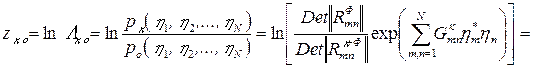
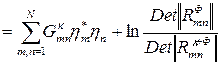где G^к_mn = Q^Ф_mn – Q^к+ф_mn – элементы матрицы обработки коррелированного портрета К-го класса.

Например, при N=2 корреляционная матрица фона

,

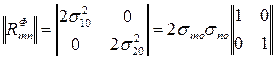корреляционная матрица К-го портрета

,

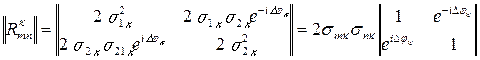корреляционная матрица К-го портрета и фона

,

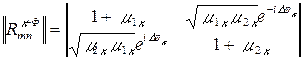обратная корреляционная матрица фона

,

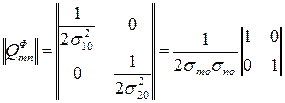обратная корреляционная матрица К-го портрета и фона

,

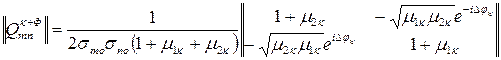матрица обработки сильно коррелированного портрета К-го класса

.

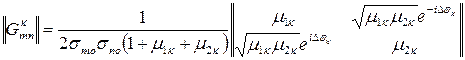Можно показать, что при произвольном N элементы матрицы обработки сильно коррелированного портрета К-го класса определяется выражением:

.

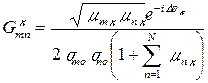Учитывая, что отношение определителей матриц

,

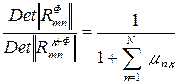искомый алгоритм оптимальной обработки сильно коррелированного портрета К-го класса может быть представлен следующим образом:

,

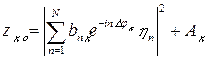где 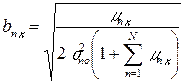- весовые коэффициенты, 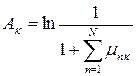- слагаемые смещения.

Полученный алгоритм обработки свидетельствует о том, что оптимальная обработка сильно коррелированных портретов сводится к их взвешенному когерентному накоплению со смещением, причем весовые коэффициенты и слагаемое смещения определяются априорно известными сведениями об эталонных портретов, т. е. Сведениями об относительной интенсивности их комплексных амплитуд и фазовых соотношений между ними. Структура устройства оптимальной обработки сильно коррелированного портрета показана на рис. 13.3.

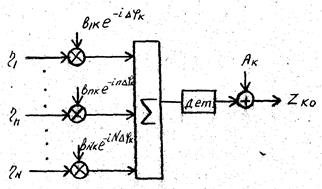
Рис. 13.3. Структура оптимальной обработки сильно коррелированного портрета

Как и в предыдущем случае некоррелированных портретов, рассмотрим целесообразность выбора весовых коэффициентов b_nк и слагаемого смещения А_к при оптимальной обработке сильно коррелированных портретов. Для этого рассмотрим среднее значение случайной величины Z_кℓ = Z_ко – Z_ℓo , лежащей в основе принятия решения, при условии наличия на входе устройства распознавания сильно коррелированного портрета К-го класса:

,

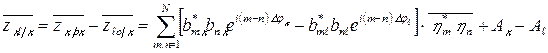отсюда с учетом 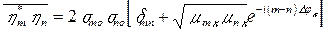находим

.

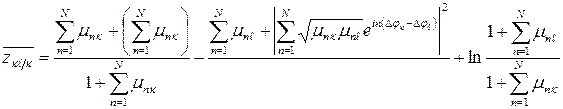Учитывая, что

,

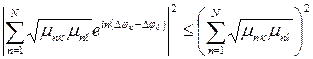а также учитывая неравенство Буняковского-Коши, согласно которому

,

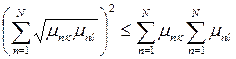находим

,

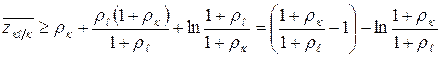где , .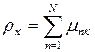

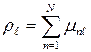Вводя понятие контрастности сильно коррелированных портретов К-го и ℓ-го классов

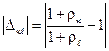
и используя разложение 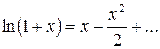, находим

.

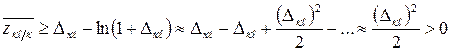Таким образом, как и в случае некоррелированных портретов, при определенном выборе весовых коэффициентов b_к и слагаемого смещения А_к, рекомендуемом результатами синтеза, случайная величина Z_ко на выходе К-го канала при условии наличия портрета К-го класса в среднем всегда больше, чем на выходе любого другого ℓ≠к канала, и, следовательно, с вероятностью больше 0.5 будет приниматься решение о наличии портрета К–го класса, т.е. правильная классификация К-го портрета будет осуществляться даже в условиях его относительной энергетической недостаточности.