Уравнения Максвелла в комплексной форме
Если Н и Е изменяются во времени синусоидально, то можно воспользоваться символическим методом и записать в иной форме.
Пусть Н= 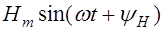 и
и 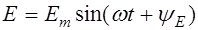 .
.
Можно записать 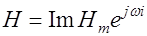 (Im – мнимая часть) или, условно,
(Im – мнимая часть) или, условно, 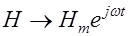 (
( 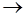 значок соответствия), где комплексная амплитуда
значок соответствия), где комплексная амплитуда 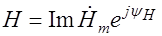 . В свою очередь
. В свою очередь 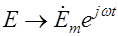 .
.
Так как напряженности Е и Н, кроме того, что они меняются во времени по синусоидальному закону, являются функциями векторными, то есть определенным образом ориентированными в пространстве векторами, то над ними ставят стрелку и точку: 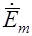 и
и 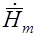 . Стрелка означает, что речь идет о векторе в пространстве, а точка – о том, что проекции этого вектора на любую из координатных осей во времени изменяются синусоидально.
. Стрелка означает, что речь идет о векторе в пространстве, а точка – о том, что проекции этого вектора на любую из координатных осей во времени изменяются синусоидально.
Тогда 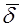 можно заменить на
можно заменить на 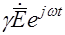 , а
, а
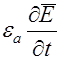 – на
– на 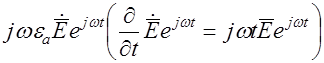 и
и
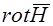 – на
– на 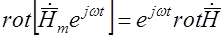 .
.
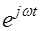 как постоянную величину, не зависящую от координат, можно вынести за знак ротора). При этом первое уравнение Максвелла запишем так:
как постоянную величину, не зависящую от координат, можно вынести за знак ротора). При этом первое уравнение Максвелла запишем так:
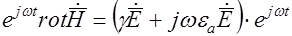 .
.
После сокращения на 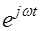 получим
получим
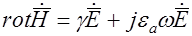 . . | (45.1) |
Аналогично, второе уравнение Максвелла в комплексной форме
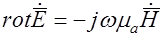 . . | (45.2) |
2. Теорема Умова – Пойнтинга для мгновенных значений
Теорема Умова – Пойнтинга описывает энергетические соотношения в поле. Она связывает изменение энергии в каком-либо объеме с потоком ее через поверхность, ограничивающую этот объем.
Известно, что энергия электрического поля в единице объема равна 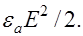 Энергия магнитного поля в единице объема –
Энергия магнитного поля в единице объема – 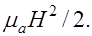 Суммарная энергия электромагнитного поля в объеме V
Суммарная энергия электромагнитного поля в объеме V
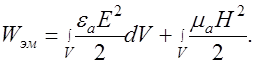 | (45.3) |
Она непрерывно изменяется во времени.
Изменение (увеличение) энергии в указанном объеме
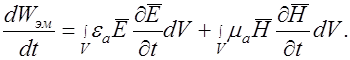
Запишем уравнения Максвелла для среды с 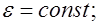
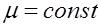 и
и 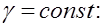
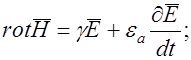
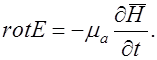
Из этих уравнений найдем:
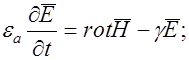
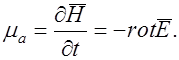
Тогда изменение энергии электромагнитного поля можно выразить следующим образом:
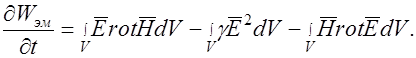
Из курса векторного анализа известно, что
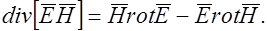
Следовательно,
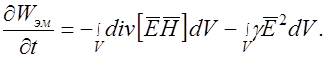
Обозначим векторное произведение
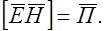
Его называют вектором Пойнтинга.
Величина П измеряется в ваттах на квадратный метр (вт/м2).
По теореме Остроградского
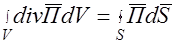
и, следовательно,
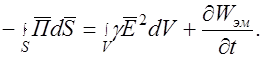 | (45.4) |
Полученное выражение носит название теоремы Умова – Пойнтинга: поток вектора Пойнтинга, входящий в замкнутую поверхность S, равен сумме двух мощностей, одна из которых 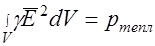 является мощностью тепловых потерь внутри объема V, ограниченного поверхностью S, а другая
является мощностью тепловых потерь внутри объема V, ограниченного поверхностью S, а другая 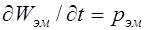 соответствует изменению энергии электромагнитного поля в том же объеме.
соответствует изменению энергии электромагнитного поля в том же объеме.
Мощность тепловых потерь ртепл всегда положительна. Мощность рэм, соответствующая изменению энергии электромагнитного поля, может быть и положительной и отрицательной. Если она положительна, то электромагнитная энергия внутри объема V увеличивается.
Положительная нормаль к замкнутой поверхности и вектор 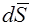 направлены в наружную сторону. Поэтому, для того, чтобы поток вектора
направлены в наружную сторону. Поэтому, для того, чтобы поток вектора 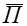 , входящий через поверхность S, был положительным, вектор
, входящий через поверхность S, был положительным, вектор 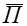 должен быть преимущественно направлен внутрь объема V.
должен быть преимущественно направлен внутрь объема V.
При выводе теоремы Умова – Пойнтинга мы предполагали, что в объеме, ограниченном замкнутой поверхностью S, нет источников энергии. Если в объеме V такие источники имеются, причем мгновенная мощность источников равна рист, то теорему необходимо записать следующим образом:
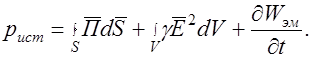
Мощность источников в объеме V равна сумме мощностей: тепловых потерь, мощности изменения энергии электромагнитного поля в объеме V и мощности энергии, выходящей через граничную поверхность S рассматриваемого объема.
3. Теорема Умова – Пойнтинга в комплексной форме
