Давление пара растворителя над раствором ниже, чем над чистым растворителем, т. е. P10>p1
Формулировка з-на Рауля № 1: «Давление насыщенного пара над раствором пропорционально молярной доле растворителя».
P1 = P1 0 · X1 (1), где P1 и P1 0 – давление пара растворителя над раствором и над чистым растворителем соответственно; X1 – молярная доля растворителя.
Т. к. X1 = 1 – X2, то p1 = p10(1 – X2) = p10 – p10·X2, следовательно, X2=(p10-p1)/p10, где p1 0 – давление пара растворителя в чистом состоянии; p1 – давление его над раствором; X2 – молярная доля растворённого вещества.
Формулировка з-на Рауля № 2: «Относительное понижение давления насыщенного пара над раствором равно молярной доле растворённого вещества».
Растворы, подчиняющиеся з-ну Рауля при всех температурах и концентрациях, называются идеальными.
C ростом давления пара и с увеличением концентрации раствора наблюдаются отклонения от з-на Рауля.
9. Температура кипения и эбуллиоскопическая постоянная
Температура кипения – температура, при которой давление насыщенного пара над чистым растворителем и над раствором будет равно внешнему давлению.
Температура кипения идеального раствора выше температуры кипения чистого растворителя.
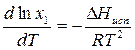
ΔТкип = Е·Cm, где Е – эбуллиоскопическая постоянная, которая зависит от природы растворителя и не зависит от природы растворённого вещества.
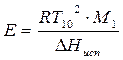, где М1 – молярная масса растворителя (летучего компонента), Т01 – температура кипения чистого растворителя.
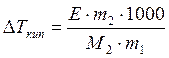, следовательно, молярная масса растворённого вещества M2 = E·m2·1000/(∆Tкип·m1)
10. Температура замерзания и криоскопическая постоянная
Условие кристаллизации:жидкость кристаллизуется при той температуре, при которой давление пара растворителя над раствором и над твёрдым растворителем будет одинаково.
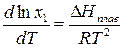
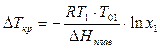
ΔТкр = K·Cm, где K – криоскопическая постоянная, не зависящая от природы растворённого вещества, а зависящая от природы растворителя
Если T1≈T01, тогда K=R(T01)2/∆Hпл·1000
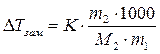(1 – растворитель, 2 – растворённое вещество)
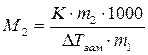
11. Правило фаз Гиббса, расчёт степеней свободы
Правило фаз Гиббса гласит: «В равновесной термодинамической системе, на которую из внешних факторов оказывают влияние только температура T и давление p, число термодинамических степеней свободы равно: число компонентов минус число фаз плюс два».
с = k – ф + 2, где с – число степеней свободы; k – число компонентов; ф – число фаз.
Если p или T = const, то с = k – ф + 1
Если T = const или p = const, то условная степень свободы Сусл = k – ф
12. Расчёт изменения энтропии для различных процессов
1) T, p = const
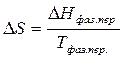
2) Изменение S при нагревании от T1 до T2 при V = const
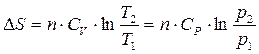
3) Изменение S при нагревании от T1 до T2 при p = const
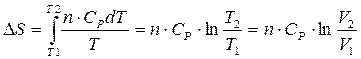
4) Изменение S для различных процессов
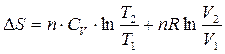
Если T = const, то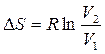 
5) Изменение S при смешении невзаимодействующих газов
2 идеальных газа в сосуде, разделённом пористой перегородкой, p и T газов одинаковы.
Газы будут взаимно диффундировать через отверстие перегородки и через некоторый промежуток времени в обоих частях образуется равномерная смесь газов.
(n1 +n2) молей газа займут объём (V1 + V2).
Чтобы вычислить ∆S при взаимной диффузии газов, необходимо вычислить ∆S каждого газа при изотермическом обратимом процессе, после чего просуммировать.
, 
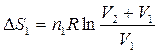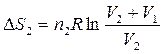
Тогда ∆S = ∆S1 + ∆S2 = R[n1ln(V1+V2)/V1 + n2ln(V1+V2)/V2]
Молярная доля 1-го газа: x1 = n1/(n1+n2); n = pV/RT
В данных конкретных условиях x1 = V1/(V1+V2), x2 = V2/(V1+V2)
Получается, ∆S = -R∑nilnxi, если у нас i газов.
Если xi = 0,4, то ln0,4 < 0.
Ввиду знака «-» в формуле ∆S > 0 при xi < 1.