Ядерная модель атома. Постулаты Бора.

ЛЕКЦИИ ПО АТОМНОЙ ФИЗИКЕ

Лекция 1.

Тепловое излучение. Формула Планка. Фотоэффект. Тормозное рентгеновское излучение.

К середине 19-го века волновая природа света считалась доказанной окончательно. Однако это представление оказалось недостаточным для истолкования всей совокупности оптических явлений. Впервые это обнаружилось при рассмотрении проблемы равновесного теплового излучения. Попытки решить эту проблему в рамках волновых представлений окончились неудачей. Выход был найден М.Планком, предположившим, что излучение и поглощение света веществом происходит не непрерывно, а конечными порциями, называемыми квантами энергии, получившими позднее название квантов света или фотонов.

Оказалось, что понятия классической физики, возникшие на основе изучения макроскопических объектов, неприменимы или ограниченно применимы в области атомных масштабов. В этой области потребовались новые представления и законы, которые и были найдены. Они составили основу новой квантовой физики.

Тепловое излучение и люминесценция

Излучение телами электромагнитных волн (свечение тел) может осуществляться за счет различных видов энергии. Самым распространенным является тепловое излучение, т. е. испускание электромагнитных волн за счет внутренней энергии тел. Все остальные виды свечения, возбуждаемые за счет любого вида энергии, кроме внутренней (тепловой), объединяются под общим названием «люминесценция».

Окисляющийся на воздухе фосфор светится за счет энергии, выделяемой при химическом превращении. Такой вид свечения называется хемилюминесценцией. Свечение, возникающее в газах и твердых телах под воздействием электрического поля, называется электролюминесценцией. Свечение твердых тел, вызванное бомбардировкой их электронами, называют катодолюминесценцией. Свечение, возбуждаемое поглощаемым телом электромагнитным излучением, называется фотолюминесценцией.

Тепловое излучение имеет место при любой температуре, однако при невысоких температурах излучаются практически лишь длинные (инфракрасные) электромагнитные волны.

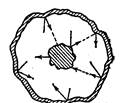Окружим излучающее тело оболочкой с идеально отражающей поверхностью (рис. 1.1). Воздух из оболочки удалим. Отраженное оболочкой излучение, упав на тело, поглотится им (частично или полностью). Следовательно, будет происходить непрерывный обмен энергией между телом и заполняющим оболочку излучением. Если распределение энергии между телом и излучением остается неизменным для каждой длины волны, состояние системы тело — излучение будет равновесным. Опыт показывает, что единственным видом излучения, которое может находиться в равновесии с излучающими телами, является тепловое излучение. Все Рис.1.1.

остальные виды излучения оказываются неравновесными.

Способность теплового излучения находиться в равновесии с излучающими телами обусловлена тем, что его интенсивность возрастает при повышении температуры. Допустим, что равновесие между телом и излучением нарушено и тело излучает энергии больше, чем поглощает. Тогда внутренняя энергия тела будет убывать, что приведет к понижению температуры. Это в свою очередь обусловит уменьшение количества излучаемой телом энергии. Температура тела будет понижаться до тех пор, пока количество излучаемой телом энергии не станет равным количеству поглощаемой энергии. Если равновесие нарушится в другую сторону, т. е. количество излучаемой энергии окажется меньше, чем поглощаемой, температура тела будет возрастать до тех пор, пока снова не установится равновесие. Таким образом, нарушение равновесия в системе тело — излучение вызывает возникновение процессов, восстанавливающих равновесие.

Иначе обстоит дело в случае люминесценции. Покажем это на примере хемилюминесценции. Пока протекает обусловливающая излучение химическая реакция, излучающее тело все больше и больше удаляется от первоначального состояния. Поглощение телом излучения не изменит направления реакции, а наоборот, приведет к более быстрому (вследствие нагревания) протеканию реакции в первоначальном направлении. Равновесие установится лишь тогда, когда будет израсходован весь запас реагирующих веществ и свечение, обусловленное химическими процессами, заменится тепловым излучением.

Итак, из всех видов излучения равновесным может быть только тепловое излучение. К равновесным состояниям и процессам применимы законы термодинамики. Поэтому тепловое излучение должно подчиняться некоторым общим закономерностям, вытекающим из принципов термодинамики.

Характеристики излучения и излучающего тела.

Обозначим через u плотность энергии излучения, т.е. количество энергии в единице объема. Излучение представляет собой совокупность волн различных частот (бегущих или стоячих). Поскольку плотность энергии излучения разной частоты различна, обозначим 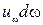объемную плотность лучистой энергии, приходящийся на интервал частот 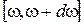. Очевидно, что

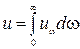. (1.1)

Интенсивность теплового излучения характеризуется величиной потока энергии, измеряемой в ваттах. Энергия излучения связана с излучающим телом. Поток энергии, испускаемый единицей поверхности излучающего тела по всем направлениям (в пределах телесного угла 2π), называют энергетической светимостью тела. Мы будем обозначать эту величину буквой R. Энергетическая светимость является функцией температуры.

Излучение состоит из волн различных частот ω (или длин 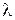). Обозначим поток энергии, испускаемый единицей поверхности тела в интервале частот dω, через dR_ω. При малом интервале dω поток dR_ω будет пропорционален dω:

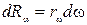. (1.2)

Величина r_ω называется испускательной способностью тела. Как и энергетическая светимость, испускательная способность сильно зависит от температуры тела. Таким образом, r_ω есть функция частоты и температуры. Испускательная способность это поток энергии, излучаемый единицей поверхности тела во всех направлениях в единичном интервале частот вблизи .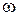

Энергетическая светимость связана с испускательной способностью формулой

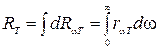(1.3)

(чтобы подчеркнуть, что энергетическая светимость и испускательная способность зависят от температуры, мы их снабдили индексом Т).

Пусть на элементарную площадку поверхности тела падает поток лучистой энергии dФ_ω, обусловленный электромагнитными волнами, частота которых заключена в интервале dω. Часть этого потока 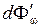будет поглощена телом. Безразмерная величина

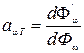(1.4)

называется поглощательной способностью тела. Поглощательная способность тела есть функция частоты и температуры. Поглощательная способность это доля энергии, поглощенная телом из падающего на него потока.

По определению a_ωT не может быть больше единицы. Для тела, полностью поглощающего упавшее на него излучение всех частот, a_ωT = 1. Такое тело называется абсолютно черным. Будем в дальнейшем обозначать испускательную и поглощательную способность абсолютно черного тела 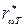и 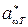. Тело, для которого a_ωT ≡ a_T =const<1, называют серым. Если 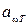= 0, это или абсолютно прозрачное тело или абсолютно зеркальное.

Между испускательной и поглощательной способностями любого тела имеется связь. В этом можно убедиться, рассмотрев следующий эксперимент. Пусть внутри замкнутой оболочки, поддерживаемой при постоянной температуре Т, помещены несколько тел (рис.1.2). Полость внутри оболочки эвакуирована 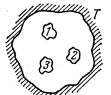(там отсутствуют молекулы какого-либо вещества), Рис.1.2

что тела могут обмениваться энергией между собой и с оболочкой лишь путем испускания и поглощения электромагнитных волн. Опыт показывает, что такая система через некоторое время придет в состояние теплового равновесия — все тела примут одну и ту же температуру, равную температуре оболочки Т. В таком состоянии тело, обладающее бóльшей испускательной способностью r_ωT, теряет в единицу времени с единицы поверхности больше энергии, чем тело, обладающее меньшей r_ωT. Поскольку температура (а, следовательно, и энергия) тел не меняется, то тело, испускающее больше энергии, должно и больше поглощать, т. е. обладать большей a_ωT. Таким образом, чем больше испускательная способность тела r_ωT, тем больше и его поглощательная способность a_ωT. Отсюда вытекает соотношение

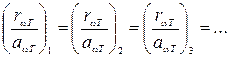, (1.5)

где индексы 1, 2, 3 и т. д. относятся к разным телам.

Соотношение (1.5) выражает установленный Кирхгофом закон, который формулируется следующим образом: отношение испускательной и поглощательной способностей не зависит от природы тела, оно является для всех тел одной и той же (универсальной) функцией частоты (длины волны) и температуры:

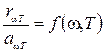. (1.6)

Сами величины r_ωT и a_ωT могут меняться чрезвычайно сильно при переходе от одного тела к другому. Отношение же их оказывается одинаковым для всех тел. Это означает, что тело, сильнее поглощающее какие-либо лучи, будет эти лучи сильнее и испускать (не следует смешивать испускание лучей с их отражением). Функция называется функцией Кирхгофа.

Для абсолютно черного тела по определению a_ωT = 1. Следовательно, из формулы (1.6) вытекает, что r_ωT для такого тела равна f(ω, Т). Таким образом, универсальная функция Кирхгофа f(ω, Т) есть не что иное, как испускательная способность абсолютно черного тела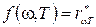

Абсолютно черных тел в природе не существует. Однако можно создать устройство, сколь угодно близкое по своим свойствам к абсолютно черному телу. Такое устройство представляет собой почти замкнутую полость, снабженную малым отверстием (рис. 1.3). Излучение, проникшее внутрь через отверстие, прежде чем выйти обратно из отверстия, претерпевает многократные отражения. При каждом отражении часть Рис.1.3

энергии поглощается, в результате чего практически все излучение любой частоты поглощается такой полостью.

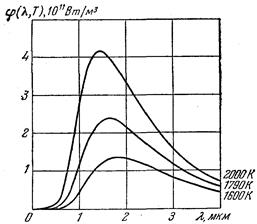Согласно закону Кирхгофа испускательная способность такого устройства очень близка к f(ω, Т), причем Т означает температуру стенок полости. Таким образом, если стенки полости поддерживать при некоторой температуре Т, то из отверстия выходит излучение, весьма близкое по спектральному составу к излучению абсолютно черного тела при той же температуре. Проводя эксперимент и разлагая это излучение в спектр с помощью дифракционной решетки можно измерить интенсивность различных участков спектра. Такой эксперимент дает вид функции f(ω,Т) (или φ(λ, Т)). Результаты таких опытов приведены на рис.1.4. Разные Рис.1.4

кривые относятся к различным значениям температуры Т абсолютно черного тела. Площадь, охватываемая кривой, дает энергетическую светимость абсолютно черного тела при соответствующей температуре.

Из рис.1.4 следует, что энергетическая светимость абсолютно черного тела сильно возрастает с температурой. Максимум испускательной способности с увеличением температуры сдвигается в сторону более коротких волн.

Равновесная плотность энергии излучения

Рассмотрим излучение, находящееся в равновесии с веществом. Для этого представим себе эвакуированную полость, стенки которой поддерживаются при постоянной температуре Т. В равновесном состоянии энергия излучения будет распределена в объеме полости с определенной плотностью u = u(T). Спектральное распределение этой энергии можно охарактеризовать функцией u(ω,T), определяемой условием du_ω= u(ω,T) d 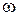, где du_ω — доля плотности энергии, приходящаяся на интервал частот dω. Полная плотность энергии u(T) связана с функцией u(ω,T) формулой (1.1).

Из термодинамических соображений следует, что равновесная плотность энергии излучения u(T) зависит только от температуры и не зависит от свойств стенок полости.

Равновесная плотность энергии излучения u связана с энергетической светимостью абсолютно черного тела R* простым соотношением

(1.7)

Равенство (1.7) должно выполняться для каждой спектральной составляющей излучения. Отсюда вытекает, что

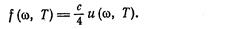(1.8)

Эта формула связывает испускательную способность абсолютно черного тела с равновесной плотностью энергии теплового излучения.

Формула Рэлея — Джинса.

Английские физики Джон Уильям Рэлей и Джеймс Хопвуд Джинс сделали попытку определить равновесную плотность излучения u(ω, Т), исходя из теоремы классической статистики о равнораспределении энергии по степеням свободы. Они предположили, что на каждое электромагнитное колебание приходится в среднем энергия, равная двум половинкам kT–одна половинка на электрическую, вторая — на магнитную энергию волны (напомним, что по классическим представлениям на каждую колебательную степень свободы приходится в среднем энергия, равная двум половинкам kТ).

Равновесное излучение в полости представляет собой систему стоячих волн. С учетом возможных видов поляризации можно найти количество стоячих волн, отнесенное к единице объема полости. Оно определяется формулой

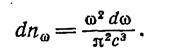(1.9)

Рэлей и Джинс, исходя из закона равнораспределения энергии по степеням свободы, приписали каждому колебанию энергию ‹ε›, равную kT. Умножив (1.9) на ‹ε›, получим плотность энергии, приходящуюся на интервал частот dω:

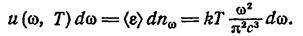
Отсюда

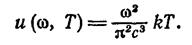(1.10)

Перейдя от u(ω, Т) к f(ω, Т), получим выражение для испускательной способности абсолютно черного тела:

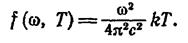(1.11)

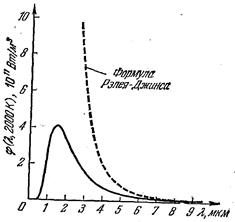Выражения (1.10) и (1.11) называются формулой Рэлея — Джинса. Эта формула удовлетворительно согласуется с экспериментальными данными лишь при больших длинах волн (малых частотах) и резко расходится с опытом для малых длин волн (на рис.1.5 сплошной линией изображена экспериментальная кривая, пунктиром кривая, построенная по формуле Рэлея — Джинса).

Интегрирование выражения (1.10) по ω в пределах от 0 до ∞ дает для равновесной плотности энергии u(Т) бесконечно большое значение. Этот результат, получивший название ультрафиолетовой катастрофы, также находится в противоречии с опытом. Равновесие между излучением и излучающим телом устанавливается при конечных значениях u(Т). Рис.1.5

Формула Планка

С классической точки зрения вывод формулы Рэлея—Джинса является безупречным. Поэтому расхождение этой формулы с опытом указывало на существование каких-то закономерностей, несовместимых с представлениями классической физики.

В 1900 г. немецкому физику Максу Планку удалось найти вид функции u(ω, Т), в точности соответствующий опытным данным:

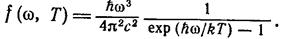(1.12)

Для этого ему пришлось сделать предположение совершенно чуждое классическим представлениям, а именно допустить, что электромагнитное излучение испускается в виде отдельных порций энергии (квантов), величина которых пропорциональна частоте излучения:

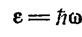(1.13)

Коэффициент пропорциональности 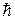получил впоследствии название постоянная Планка.

Исходя из выдвинутого предположения, Планк получил значение средней энергии излучения частоты :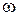

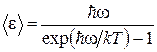, (1.14)

откуда с учетом (1.9) и следует формула Планка (1.12).

Заметим, что для малых частот, когда 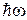« kT , выражение (1.14) дает классическое .

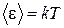Фотоэлектрический эффект.

Одним из явлений, подтверждающим гипотезу фотонов, является фотоэлектрический эффект, обнаруженный в 1887г. Г.Герцем. Сущность явления состоит в том, что при освещении ультрафиолетовыми лучами отрицательно заряженного металлического тела оно теряет отрицательный заряд. Если тело не было заряжено, то при освещении оно заряжается положительно до потенциала в несколько вольт. Было доказано, что при освещении тела теряют электроны. Это явление получило название фотоэлектрического эффекта или короче фотоэффекта.

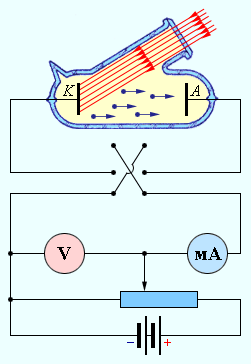
На рис 1.6 показана принципиальная схема экспериментальной установки для исследования фотоэффекта. Электроды помещают в вакуумированный баллон. Фотоэлектроны, вырванные светом из катода, ускоряются электрическим Рис.1.6 полем и замыкают цепь.

На рис 1.7 представлена вольтамперная характеристика фотоэлемента (зависимость силы фототока от напряжения между катодом и анодом).

При увеличении напряжения характеристика переходит в горизонтальную прямую, которой соответствует максимальный ток – ток насыщения. Ток насыщения достигается тогда, когда все электроны, вырванные светом с поверхности катода, попадают на анод. Величина тока насыщения определяется только количеством вырванных электронов, т.е. пропорциональна интенсивности падающего излучения. На рис.1.7 интенсивность, соответствующая кривой 2 больше чем 1. Пологий ход кривой указывает на то, что электроны вылетают из катода с различными по величине скоростями. Доля электронов, отвечающая силе тока при нулевом напряжении, обладает скоростями, достаточными для того, чтобы долететь до анода «самостоятельно», без помощи ускоряющего поля. Для обращения силы тока в нуль нужно приложить задерживающее напряжение 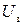. При таком напряжении ни одному из электронов, даже обладающему при вылете из электрода наибольшим значением скорости 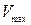не удается преодолеть задерживающее поле и достигнуть анода. Поэтому можно написать

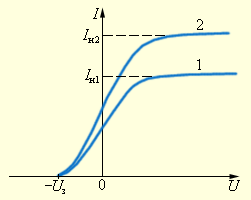
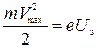, (1.15)

Рис.1.7 где т – масса электрона, е – его заряд.

Экспериментально были установлены следующие законы фотоэффекта.

1. При фиксированной частоте излучения число электронов, вылетающих в единицу времени с единицы поверхности фотокатода (а значит и сила тока насыщения) прямо пропорциональна плотности светового потока.

2. Максимальная энергия фотоэлектронов и их скорость не зависят от плотности светового потока и линейно возрастают с ростом частоты падающего излучения.

3. Существует граничная частота излучения 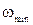, ниже которой для данного материала катода фотоэффект отсутствует, независимо от плотности светового потока и продолжительности облучения катода. Эта частота называется красной границей фотоэффекта.

4 Исследование времени запаздывания появления фототока относи- тельно начала облучения привели к значению меньше .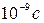

Можно было бы дать объяснение этого явления с точки зрения волновой природы излучения. Свободные электроны, находящиеся в металле, удерживаются в нем задерживающим полем, существующим на границе металла. Работа выхода электрона из металла составляет несколько электрон-вольт. В электрическом поле световой волны свободные электроны приходят в колебания. Когда энергия колебаний сделается достаточно большой, электрон может преодолеть задерживающее поле и выйти из металла. (Для связанных электронов все будет происходить аналогично, но зависимость энергии колебаний от частоты будет носить более сложный, резонансный характер.)

Однако такое объяснение не согласуется с опытом. Поскольку энергия электрона заимствуется от волны, то она должна зависеть от интенсивности волны. Но это противоречит второму экспериментальному закону.

Другое расхождение с экспериментом получается, если оценить время возникновения фотоэффекта. Расчеты показывают, что фотоэффект должен протекать с запаздыванием порядка нескольких секунд, что также противоречит экспериментальным данным.

Следующее противоречие связано с наличием красной границы фотоэффекта. Если электрон совершает под действием волны вынужденные колебания, то амплитуда колебаний, а, следовательно, и его энергия, определяется резонансной кривой. Поэтому необходимое значение амплитуды можно получить в некотором интервале частот вблизи резонансной, т.е. должно существовать не только минимальное, но и максимальное значение частоты, при которой наблюдается фотоэффект.

Указанные трудности отпадают, если фотоэффект рассматривать с фотонной точки зрения. Взаимодействуя с электроном металла, фотон может обмениваться с ним энергией и импульсом. Такой процесс напоминает удар шаров, а потому его называют столкновением. Фотоэффект возникает при неупругом столкновении. При таком столкновении фотон поглощается, а его энергия передается электрону. Таким образом, электрон приобретает энергию не постепенно, а сразу – в результате единичного акта столкновения. Этим объясняется безынерционность фотоэффекта.

Пусть электрон получил от фотона энергию, равную 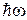. За счет этой энергии он может преодолеть потенциальный барьер на границе металла (совершить работу выхода А) и вылететь из металла, имея энергию 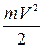. Тогда можно записать соотношение, которое называют уравнением Эйнштейна для фотоэффекта

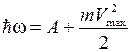. (1.16)

Из этой формулы вытекают два следствия.

1. Максимальная кинетическая энергия вырванных электронов линейно зависит от частоты света и не зависит от его интенсивности. Интенсивность оказывает влияние только на количество вырванных электронов.

2. Существует низкочастотная граница фотоэффекта (красная граница) 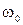, ниже которой фотоэффект не наблюдается. Она зависит от облучаемого тела и состояния его поверхности .

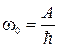Таким образом, если представлять излучение как поток частиц (фотонов), то выводы теории согласуются с экспериментом.

Тормозное рентгеновское излучение

Если энергия кванта значительно превышает работу выхода, то уравнение Эйнштейна принимает более простой вид

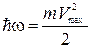. (1.17)

Эту формулу можно интерпретировать и иначе: не как переход энергии кванта в кинетическую энергию электрона. А наоборот. Как переход кинетической энергии электронов, ускоренных разностью потенциалов U, в энергию квантов, возникающих при резком торможении электронов в металле. Тогда

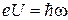. (1.18)

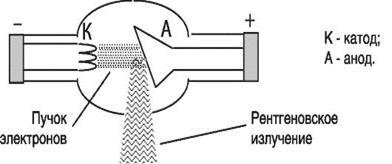
Именно такой процесс происходит в рентгеновской трубке. Она представляет собой вакуумный баллон, в котором находится нагреваемый током катод – источник термоэлектронов, и расположенный напротив анод, часто называемый антикатодом.

Рис.1.8

Ускорение электронов осуществляется высоким напряжнием U,создаваемым между катодом и антикатодом. Под действием напряжения U электроны разгоняются до энергии eU. Попав в металлический антикатод, электроны резко тормозятся, вследствие чего возникает так называемое тормозное рентгеновское излучение. Спектр этого излучения при разложении по длинам

волн оказывается сплошным.

На рис.1.9 показаны экспериментальные кривые распределения мощности излучения Р по длинам волн 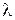, полученные для разных значений ускоряющего напряжения.

Согласно классической электродинамике при торможении электрона должны возникать излучения всех длин волн от нуля до бесконечности. Длина волны, на которую приходится максимум мощности излучения, должна уменьшиться по мере увеличения скорости электронов. В основном это подтверждается на опыте. Однако со стороны коротких волн кривая мощности резко обрывается при некотором значении длины волны. Эта длина волны называется коротковолновой границей тормозного рентгеновского излучения. Коротковолновая граница не зависит от материала антикатода, а определяется только напряжениРис.1.9 ем на трубке. Если увеличивать напряжение выше определенного предела, зависящего от материала антикатода, то на сплошное излучение накладываются узкие спектральные линии, составляющие так называемое характеристическое излучение. Но и в этом случае коротковолновая граница существует.

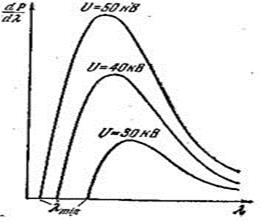
Существование такой границы является одним из наиболее ярких проявлений корпускулярных свойств излучения. Действительно, если излучение возникает за счет энергии, теряемой электроном при торможении, то величина кванта 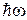не может быть больше энергии электрона eU. Отсюда следует, что частота излучения не может превышать значения 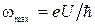. Значит, длина волны излучения не может быть меньше, чем

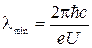. (1.19)

По измерению зависимости граничной частоты от ускоряющего напряжения можно определить значение постоянной Планка. При этом получается хорошее согласие со значениями, найденными из теплового излучения и фотоэффекта.

Фотоны

Рассмотренные опыты подтвердили гипотезу о световых квантах – фотонах. Излучение частоты 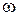- это поток фотонов с энергией 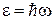. Свет распространяется в вакууме со скоростью с. Значит такова же скорость фотонов. Согласно теории относительности полная энергия любой частицы, движущейся со скоростью V, определяется как 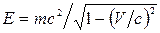. В случае фотона V=c, и знаменатель этого выражения обращается в нуль. Для фотона, имеющего конечную энергию, это возможно лишь при условии т=0. Таким образом, масса покоя фотона равна нулю.

Воспользовавшись связью между энергией Е и импульсом р движущейся частицы 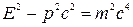, приходим к выводу, что фотон (т=0) обладает импульсом 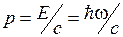. Замечая, что 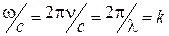(k – волновое число), запишем 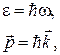(1.20)

где 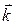- волновой вектор.

Частота и волновой вектор характеризуют волновые свойства излучения, а энергия и импульс – корпускулярные свойства.

Из опытных фактов следует, что при взаимодействии с веществом свет обнаруживает корпускулярные свойства. Однако, представление о свете как о потоке классических корпускул несовместимо с классическими представлениями об электромагнитных волнах (которые подтверждаются в явлениях интерференции и дифракции). Сосуществование этих свойств не может быть логически непротиворечиво объяснено классической физикой. Представить себе такой объект, который совмещал бы несовместимое в воображении невозможно. При этом фотон проявляет свои корпускулярно – волновые свойства в разных соотношениях: в области длинных волн - в основном волновые свойства, а в области коротких волн – корпускулярные.

Итак, фотон нельзя представить моделью, описываемой классическим образом. Он является квантовым объектом, который нельзя представить с помощью классических образов.

Лекция 2

Ядерная модель атома. Постулаты Бора.