Энергия заряженного конденсатора

Процесс возникновения на обкладках конденсатора зарядов +q и –q можно представить так, что от одной обкладки последовательно отнимаются порции заряда 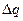и перемещаются на другую обкладку. Работа переноса очередной порции равна:

,

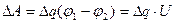где U – напряжение на конденсаторе. Заменяя U через отношение заряда к емкости и переходя к дифференциалам, получим:

.

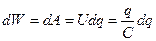Интегрируя, получим:

.

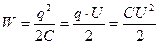Энергия электрического поля

Энергию конденсатора можно выразить через величины, характеризующие электрическое поле в зазоре между обкладками. Сделаем это для плоского конденсатора. Подставим в выражение для энергии конденсатора выражения для емкости плоского конденсатора, тогда:

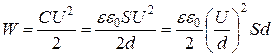. (14.23)

Так как 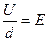, а S·d=V – объем, занимаемый полем, то можно написать:

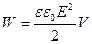. (14.24)

Формула (14.23) связывает энергию конденсатора с зарядом на его обкладках, формула (14.24) – с напряженностью поля. Логично поставить вопрос: где же локализована (т.е. сосредоточена) энергия, что является носителем энергии – заряды или поле? В пределах электростатики, изучающей постоянные во времени поля неподвижных зарядов, дать ответ на этот вопрос невозможно. Постоянные поля и обусловившие их заряды не могут существовать обособленно друг от друга. Однако меняющиеся во времени поля могут существовать независимо от возбудивших их зарядов и распространяться в пространстве в виде электромагнитных волн. Опыт показывает, что электромагнитные волны переносят энергию. Следовательно, носителем энергии является поле.

Если поле однородно, заключенная в нем энергия распределяется в пространстве с постоянной плотностью 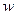равной энергии поля, деленной на заполняемый полем объем. Следовательно, плотность энергии поля плоского конденсатора:

.

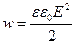Этой формуле можно придать вид:

,

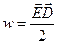заменив D (14.14), получим плотность энергии в диэлектрике:

.

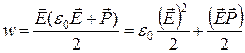Первое слагаемое совпадает с плотностью энергии поля 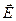в вакууме. Второе – представляет собой энергию, затрачиваемую на поляризацию диэлектрика.

ГЛАВА 15. ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК

Сила и плотность тока

Электрическим током называется любое упорядоченное (направленное) движение электрических зарядов q. В проводнике под действием приложенного электрического поля Е свободные электрические заряды перемещаются: положительные — по полю, отрицательные — против поля, т.е. в проводнике возникает электрический ток, называемыйтоком проводимости.

За направление электрического тока условно принимают направление движения положительных зарядов. Носителями электричества в проводниках–металлах являются электроны, в полупроводниках – электроны «дырки», в жидких электронах ионы, в газах ионы и электроны.

Количественной мерой электрического тока служитсила тока I — скалярная физическая величина, определяемая электрическим зарядом, проходящим через поперечное сечение проводника в единицу времени:

.

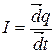Ток, сила и направление которого не изменяется со временем, называетсяпостоянным. Для постоянного тока сила тока I есть величина постоянная, поэтому

.

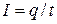Единица силы тока —ампер (А). Физическая величина, определяемая величиной тока, проходящего через единицу площади поперечного сечения проводника, перпендикулярного направлению тока, называетсяплотностью тока:

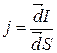, а для постоянного тока .

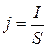Выразим силу и плотность тока через скорость 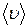упорядоченного движения зарядов в проводнике металле. Если концентрация носителей тока равна n и каждый носитель имеет элементарный заряд е, то за время 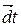через поперечное сечение S проводника переносится заряд 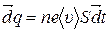. Сила тока

,

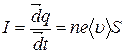а плотность тока

.

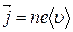Плотность тока — вектор, ориентированный по направлению тока, т.е. направление вектора 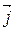совпадает с направлением упорядоченного движения положительных зарядов. Единица плотности тока - (А/м²).

Сила тока сквозь произвольную поверхность S определяется как поток вектора 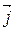, т.е.

,

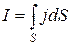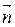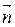где dS = dS ( — единичный вектор нормали к площадке dS, составляющей с вектором 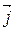угол a).

Сторонние силы. ЭДС.

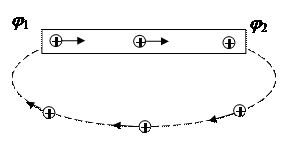Если в проводнике создать электрическое поле и не принять мер для его поддержания, то перемещение носителей заряда очень быстро приведет к исчезновению поля и прекращению тока. Для поддержания тока нужно от конца проводника с меньшим потенциалом (носители заряда предполагаются положительными) непрерывно отводить приносимые сюда током заряды, а к концу с большим потенциалом непрерывно их подводить.

То есть нужно осуществить круговорот зарядов, при котором они двигались бы по замкнутому пути. Циркуляция вектора напряжением электростатического поля равна нулю

Рис. 15.1.

.

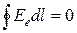Поэтому в замкнутой цепи наряду с участками, на которых положительные заряды движутся в сторону убывания j, должны иметься участки, на которых перенос положительных зарядов происходит в направлении возрастания j, т.е. против сил электростатического поля (см. рис. 15.1). Перемещение носителей на этих участках возможно лишь с помощью сил неэлектростатического происхождения, называемых сторонними силами. Таким образом, для поддержания тока необходимы сторонние силы, действующие либо на всем протяжении цепи, либо на отдельных ее участках. Они могут быть обусловлены химическими процессами, диффузией носителей заряда в неоднородной среде или через границу двух разнородных веществ, электрическими полями, порождаемыми меняющимися во времени магнитными полями.

Величина, равная работе сторонних сил, затраченной на перемещение единичного положительного заряда, называется электродвижущей силой (ЭДС) e, действующей в цепи или на ее участке

e = .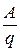

Из сопоставления этой формулы с формулой, определяющей потенциал: 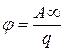, следует, что размерность ЭДС совпадает с размерностью потенциала.

Стороннюю силу 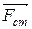, действующую на заряд 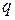, можно представить в виде

.

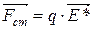Векторную величину 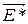называют напряженностью поля сторонних сил. Работу сторонних сил над зарядом 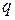на всем протяжении замкнутой цепи можно выразить следующим образом:

.

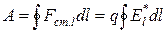Разделив эту работу на 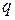, получим ЭДС действующую в цепи: e = 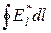. Таким образом, ЭДС, действующая в замкнутой цепи, может быть определена как циркуляция вектора напряженности поля сторонних сил.

ЭДС, действующая на участке 1-2, очевидно, равна e₁₂ = .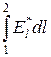

Кроме сторонних сил на заряд действуют силы электростатического поля

.

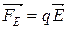Результирующая сила, действующая в каждой точке цепи на заряд 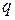, равна

.

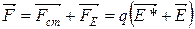Работа, совершаемая этой силой над зарядом 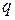на участке цепи 1-2, дается выражением

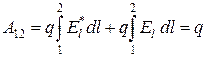e₁₂ .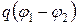

Величина, численно равная работе, совершаемой электростатическими и сторонними силами при перемещении единичного положительного заряда, называется падением напряжения или просто напряжением 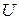на данном участке цепи

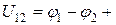e₁₂.

При отсутствии сторонних сил напряжение 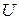совпадает с разностью потенциалов .

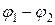Закон Ома

Немецкий физик Г. Ом (1787—1854) экспериментально установил в 1826г., что сила тока I, текущего по однородному металлическому проводнику (т.е. проводнику, в котором не действуют сторонние силы), пропорциональна напряжению U на концах проводника:

,

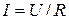где R — электрическое сопротивление проводника. Это уравнение выражает закон Ома для участка цепи(не содержащего источника э.д.с.): сила тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника. Эта формула позволяет установить единицу сопротивления — ом (Ом): 1 Ом—сопротивление такого проводника, в котором при напряжении 1 В течет постоянный ток 1 А.

Величина 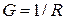называется электрической проводимостью проводника. Единица проводимости — сименс (См): 1 См—проводимость участка электрической цепи сопротивлением 1 Ом. Сопротивление проводников зависит от его размеров и формы, а также от материала, из которого проводник изготовлен. Для однородного линейного проводника сопротивление R прямо пропорционально его длине l и обратно пропорционально площади его поперечного сечения S :

,

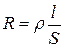где r — коэффициент пропорциональности, характеризующий материал проводника. Он называется удельным электрическим сопротивлением. Единица удельного электрического сопротивления — Ом×метр (Ом×м).

Рассмотрим неоднородный участок цепи, где действующую ЭДС на участке 1-2 обозначим через e₁₂, а приложенную на концах участка разность потенциалов — через j₁- j₂.

Если ток проходит по неподвижным проводникам, образующим участок 1-2,то работа А₁₂ всех сил (сторонних и электростатических), совершаемая над носителями тока, по закону сохранения и превращения энергии равна теплоте, выделяющейся на участке. Работа сил, совершаемая при перемещении заряда q₀ на участке 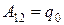1-2,

e_{12 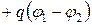.} (15.1)

ЭДС e₁₂, как и сила тока I — величина скалярная. Ее необходимо брать либо с положительным, либо с отрицательным знаком в зависимости от знака работы, совершаемой сторонними силами. Если ЭДС способствует движению положительных зарядов в выбранном направлении (в направлении 1—2), то e₁₂>0. Если ЭДС препятствует движению положительных зарядов в данном направлении, то e₁₂<0.

За время t в проводнике выделяется теплота

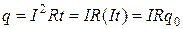. (15.2)

Из формул (15.1) и (15.2) получим 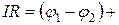e₁₂. (15.3)

Отсюда 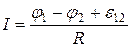. (15.4)

Выражение (15.3) или (15.4) представляет собой закон Ома для неоднородного участка цепи в интегральной форме, который является обобщенным законом Ома.

Если на данном участке цепи источник тока отсутствует (e₁₂ =0), то из (15.4) приходим к закону Ома для однородного участка цепи: 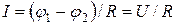(при отсутствии сторонних сил напряжение на концах участка равно разности потенциалов). Если же электрическая цепь замкнута, то выбранные точки 1 и 2 совпадают, j₁=j₂; тогда из (15.4) получаем закон Ома для замкнутой цепи: I =e/R, где e — ЭДС, действующая в цепи, R — суммарное сопротивление всей цепи. В общем случае

Рис. 15.2. R=r+R₁, где r—внутреннее сопротивление источника ЭДС, R₁ — сопротивление внешней цепи. По этому закон Ома для замкнутой цепи будет иметь вид I =e /(r+R).