Пояснение к рабочей программе. Изучение основ электродинамики традиционно начинается с электрического поля в вакууме
Изучение основ электродинамики традиционно начинается с электрического поля в вакууме. Силовой характеристикой электрического поля является напряженность 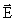 , энергетической - потенциал φ. Следует обратить внимание на связь между
, энергетической - потенциал φ. Следует обратить внимание на связь между 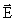 и φ . Для вычисления силы взаимодействия между двумя точными зарядами и вычисления напряженности электрического поля, созданного точечным зарядом, нужно уметь применять закон Кулона. Для вычисления напряженностей полей, созданных протяженными зарядами (заряженной нитью, плоскостью и т.д.), применяется теорема Гаусса. Для системы электрических зарядов необходимо применять принцип суперпозиции (задачи 201-220 контрольной работы).
и φ . Для вычисления силы взаимодействия между двумя точными зарядами и вычисления напряженности электрического поля, созданного точечным зарядом, нужно уметь применять закон Кулона. Для вычисления напряженностей полей, созданных протяженными зарядами (заряженной нитью, плоскостью и т.д.), применяется теорема Гаусса. Для системы электрических зарядов необходимо применять принцип суперпозиции (задачи 201-220 контрольной работы).
При изучении темы "Постоянный ток" необходимо рассмотреть во всех формах законы Ома и Джоуля-Ленца. В контрольной работе это задачи 221- 230. При изучении "Магнетизма" необходимо иметь в виду, что магнитное поле порождается движущимися зарядами и действует на движущиеся заряды. Здесь следует обратить внимание на закон Био-Савара-Лапласа. Нужно знать этот закон и уметь применять его для расчета вектора магнитной индукции - основной характеристики магнитного поля (в контрольной работе это задачи 231-240). Особое внимание следует обратить на силу Лоренца и рассмотреть движение заряженной частицы в магнитном поле (задачи 241-250).
При изучении явления электромагнитной индукции необходимо усвоить, что механизм возникновения ЭДС индукции имеет электронный характер. Основной закон электромагнитной индукции - это закон Фарадея-Ленца. Согласно этому закону, ЭДС индукции в замкнутом контуре возникает при изменении магнитного потока, сцепленного с контуром. Необходимо знать, как вычисляется магнитный поток, ЭДС индукции, как рассчитывается работа по перемещению замкнутого контура с током в магнитном поле и энергия магнитного поля (в контрольной работе задачи 251-260).
Электрические и магнитные явления связаны особой формой существования материи - электромагнитным полем. Основой теории электромагнитного поля является теория Максвелла.
В программе большое внимание уделяется изучению уравнений Максвелла. Эти уравнения могут быть записаны в двух формах: в интегральной и дифференциальной. Уравнения Максвелла удовлетворяют принципу относительности: они инвариантны относительно преобразований Лоренца. Основным следствием теории Максвелла является вывод о существовании электромагнитных волн, распространяющихся со скоростью света.
Основные формулы
Закон Кулона: где 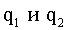 - величины точечных зарядов, - величины точечных зарядов, 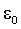 - электрическая постоянная; - электрическая постоянная; 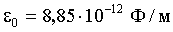 ε- диэлектрическая проницаемость изотропной среды (для вакуума ε = 1), r - расстояние между зарядами. ε- диэлектрическая проницаемость изотропной среды (для вакуума ε = 1), r - расстояние между зарядами. | 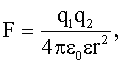 |
Напряженность электрического поля: где 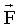 - сила, действующая на заряд - сила, действующая на заряд 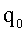 , находящийся в данной точке поля. , находящийся в данной точке поля. | 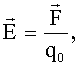 |
| Напряженность поля на расстоянии r от источника поля: точечного зарядабесконечно длинной заряженной нити с линейной плотностью заряда τ: равномерно заряженной бесконечной плоскости с поверхностной плотностью заряда σ:между двумя разноименно заряженными плоскостями | 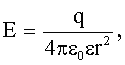 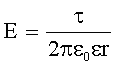 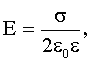 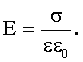 |
Потенциал электрического поля: где W - потенциальная энергия заряда 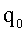 . . | 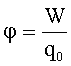 |
| Потенциал поля точечного заряда на расстоянии r от заряда: | 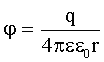 |
| По принципу суперпозиции полей, напряженность: | 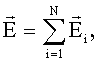 |
Потенциал: где 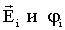 - напряженность и потенциал в данной точке поля, создаваемый i-м зарядом. - напряженность и потенциал в данной точке поля, создаваемый i-м зарядом. | 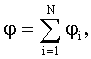 |
Работа сил электрического поля по перемещению заряда q из точки с потенциалом 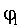 в точку с потенциалом в точку с потенциалом 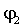 : : | 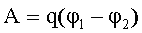 |
| Связь между напряженностью и потенциалом для неоднородного поля:для однородного поля: | 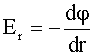 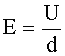 |
| Электроемкость уединенного проводника: | 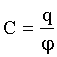 |
Электроемкость конденсатора: где 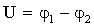 - напряжение. - напряжение. | 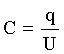 |
| Электроемкость плоского конденсатора: где S - площадь пластины (одной) конденсатора, d - расстояние между пластинами. | 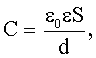 |
| Энергия заряженного конденсатора: | 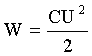 |
| Сила тока: | 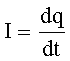 |
| Плотность тока: где S - площадь поперечного сечения проводника. | 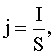 |
| Сопротивление проводника: ρ - удельное сопротивление; l - длина проводника; S - площадь поперечного сечения. | 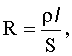 |
| Закон Ома для однородного участка цепи:в дифференциальной форме:для участка цепи, содержащего ЭДС: где ε - ЭДС источника тока, R и r - внешнее и внутреннее сопротивления цепи; для замкнутой цепи: | 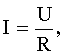 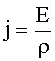 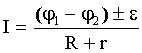 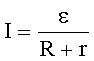 |
| Закон Джоуля-Ленца для однородного участка цепи постоянного тока: где Q - количество тепла, выделяющееся в проводнике с током, t - время прохождения тока; для участка цепи с изменяющимся со временем током: | 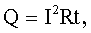 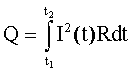 |
| Мощность тока: | 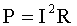 |
Связь магнитной индукции и напряженности магнитного поля: где 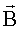 - вектор магнитной индукции, μ √ магнитная проницаемость изотропной среды, (для вакуума μ = 1), - вектор магнитной индукции, μ √ магнитная проницаемость изотропной среды, (для вакуума μ = 1), 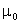 - магнитная постоянная - магнитная постоянная 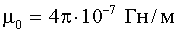 , ,  - напряженность магнитного поля. - напряженность магнитного поля. | 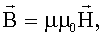 |
Магнитная индукция (индукция магнитного поля): в центре кругового тока где R - радиус кругового тока, поля бесконечно длинного прямого тока где r - кратчайшее расстояние до оси проводника; поля, созданного отрезком проводника с током где 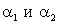 - углы между отрезком проводника и линией, соединяющей концы отрезка и точкой поля; поля бесконечно длинного соленоида где n - число витков на единицу длины соленоида. - углы между отрезком проводника и линией, соединяющей концы отрезка и точкой поля; поля бесконечно длинного соленоида где n - число витков на единицу длины соленоида. | 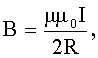 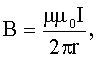 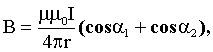 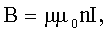 |
Сила Лоренца: по модулю где 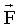 - сила, действующая на заряд, движущийся в магнитном поле, - сила, действующая на заряд, движущийся в магнитном поле,  - скорость заряда q, α - угол между векторами - скорость заряда q, α - угол между векторами 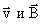 . . | 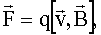 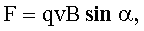 |
Поток вектора магнитной индукции (магнитный поток через площадку S): для однородного магнитного поля , где α - угол между вектором 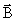 и нормалью к площадке, для неоднородного поля и нормалью к площадке, для неоднородного поля | 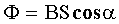 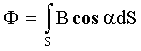 |
| Потокосцепление (полный поток): где N - число витков катушки. | 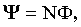 |
Закон Фарадея-Ленца: где 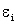 - ЭДС индукции. - ЭДС индукции. | 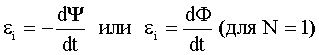 |
| ЭДС самоиндукции: где L - индуктивность контура. | 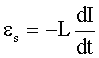 |
| Индуктивность соленоида: где n - число витков на единицу длины соленоида, V - объем соленоида. | 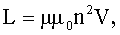 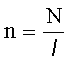 |
| Энергия магнитного поля: | 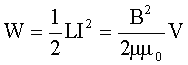 |
Заряд, протекающий по замкнутому контуру при изменении магнитного потока через контур: где 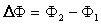 - изменение магнитного потока, R - сопротивление контура. - изменение магнитного потока, R - сопротивление контура. | 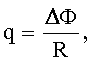 |
| Работа по перемещению замкнутого контура с током I в магнитном поле: | 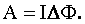 |
