Вопрос 13. Закон Максвелла для распределения молекул идеального газа по скоростям. Анализ функции распределения

В результате хаотического движения все молекулы газа движутся с разными скоростями. Но при этом средняя квадратичная скорость молекул газа, находящего в состоянии теплового равновесия при постоянной температуре, остается постоянной. Следовательно, в газе устанавливается стационарное распределение молекул по скоростям. Стационарное – независящее от времени. Этот закон на основе теории вероятности был выведен Максвеллом.

Если разбить весь диапазон скоростей молекул от 0 до бесконечности на малые интервалы dv, то на каждый интервал скорости будет приходиться некоторое число молекул dN(v) имеющих скорость в этом интервале скоростей. Если всё число молекул равно N, то функция f(v) равная относительному числу молекул, скорости которых лежать в интервале от v до v+dv.

F(v)dv=

F(v)=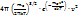

Относительное число молекул определяет вероятность того, что число молекул dN имеют скорости в интервале от v до v+dv. Если допустим N=N₀ то F(v)dv= вероятность того, что молекулы имеют скорости в интервале dv, равна площади трапеции, ограниченной на графике осью v и графиком распределения. Вся площадь под кривой равна интегралу от функции распределения от 0 до ∞.

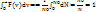– условие нормировки.

График функции имеют ярко выраженный максимум. Скорость, при которой функция распределения имеют максимум, пишется Vв – вероятнейшая скорость (наивероятнейшая) – скорость которую имеет самое большое число молекул. Vв=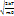
T1<T2. С увеличением температуры значение наивероятнейшей скорости увеличивается. Максимум кривой смещается вправо, т.к. площадь под кривой остаётся та же, то кривая будет растягиваться и пожаться. Число молекул, имеющих большие скорости, увеличивается. Распределение становится более равномерным.

M01 > M02. С увеличением массы молекулы или молярной массы газа максимум смещается в сторону меньших скоростей. Распределение Максвелла – наиболее вероятное распределение молекул по скоростям в условиях статистического равновесия. Температура, давление и концентрация молекул во всех точках пространства одинаковы. Это распределение определяет число частиц, которые обладают скоростями, лежащими в определенном интервале скоростей. Но нельзя сказать какая молекула, какой скоростью обладает в любой момент времени.

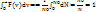– условие нормировки.

Интеграл определяет площадь под кривой функции распределения. Относительное число молекул 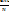равно вероятности того, что молекула имеет скорость в интервале от v до v+dv. Функция имеет максимум при значении скорости, которое называется «наиболее вероятная» или «вероятнейшая». Это означает, что максимальная доля молекул обладает скоростями, близкими к значению .

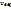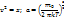
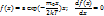
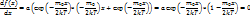
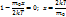
Вероятнейшая скорость: 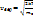, - масса молекулы.