С помощью дифракционной решетки

Цель работы: Изучение явления дифракции света, знакомство с дифракционной решеткой, определение световой волны с помощью дифракционной решетки.

Теоретическое введение:

К явлениям, в которых обнаруживается волновая природа света, относится явление дифракции. В широком смысле дифракция света – это совокупность явлений, наблюдаемых при распространении света в среде с резко выраженными неоднородностями и связанных с отклонениями от законов геометрической оптики. В узком смысле, дифракцией света называется огибание световыми волнами препятствий, линейные размеры которых сравнимы с длиной волны, и проникновение в область геометрической тени. В обычных условиях свет распространяется прямолинейно, так как освещаемые отверстия и преграды, как правило, имеют размеры, значительные по сравнению с длиной волны видимого света (0,38¸0,76 мкм). Чтобы обнаружить дифракцию света, надо создать специальные условия.

Явление дифракции было объяснено в 1815 г. Френелем путем уточнения и дополнения известного принципа Гюйгенса: каждая точка волнового фронта является точечным источником вторичной сферической волны. Огибающая поверхность всех вторичных волн в некоторый момент времени t является волновым фронтом для этого момента времени.

Френель дополнил принцип Гюйгенса идеей об интерференции вторичных волн. Согласно Френелю, при распространении в пространстве световых волн свет будет наблюдаться только в тех точках, где вторичные волны при интерференции усиливают друг друга. Для анализа дифракционной картины Френель применил прием, получивший название метода зон Френеля. Суть его состоит в том, что волновая поверхность делится на участки (зоны) таким образом, чтобы расстояния от точки наблюдения до двух соседних зон отличались на половину длины волны. Тогда вторичные волны, приходящие в точку наблюдения из соответственных точек соседних зон, будут находиться в противофазе. Поэтому амплитуда результирующих колебаний, вызванных совместным действием двух соседних зон, будет равна разности амплитуд, возбуждаемых в точке наблюдения волнами, исходящими из каждой зоны в отдельности (волны “гасят” друг друга).

Рассмотрим дифракцию света на узкой щели. Пусть на щель шириной a (рис.5.1) нормально падает монохроматическая плоская волна. После прохождения через щель волны будут распространяться по всем направлениям, т.к. согласно принципу Гюйгенса-Френеля каждая точка волновой поверхности АВ является источником вторичных сферических волн.

Выделим некоторое направление, например, под углом j к нормали и определим, каков будет результат наложения вторичных волн, если свести их в одну точку с помощью линзы Л. Для этого мысленно разобьем щель на полосы, параллельные краям так, чтобы разность хода волн от краев полосок была равна l¤2. Эти полосы в данном случае будут являться зонами Френеля. Чтобы найти число зон n, которое укладывается на ширине щели а, надо разделить разность хода D между крайними лучами (D = а sinj) на l¤2,

т.е. 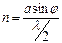(5.1)

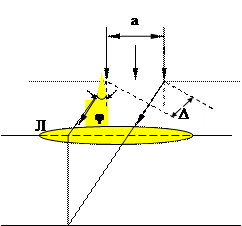Рис.5.1

Площади всех полос (зон) одинаковы, поэтому одинаковыми будут и амплитуды колебаний, возбуждаемых в фокальной плоскости линзы волнами от каждой зоны Френеля. Вместе с тем фазы колебаний, возбуждаемых волнами от соседних зон, противоположны, поэтому волны, идущие от каждой пары соседних зон, будут полностью гаситься. Следовательно, если на ширине щели уложится четное число зон, то при наложении все вторичные волны погасят друг друга, и в соответствующих направлениях интенсивность света окажется равной нулю. Если n равно нечетному числу, то действие щели эквивалентно действию одной зоны Френеля, ибо действия остальных зон взаимно компенсируются. В этом случае наблюдается максимум интенсивности света. Таким образом, вследствие дифракции за щелью вместо геометрического силуэта щели (что имело бы место в случае прямолинейного распространения света) получаются чередующиеся светлые и темные полосы. Заметим, что в прямом направлении (j=0) вся щель действует как одна зона Френеля (D =0). В этом направлении свет распространяется с наибольшей интенсивностью.

На явлении дифракции основано действие одномерной амплитудной дифракционной решетки, которая представляет собой совокупность параллельных щелей равной ширины, лежащих в одной плоскости и разделенных равными по ширине непрозрачными промежутками. Дифракционную решетку можно получить, нанося алмазом на стекле с помощью специальной делительной машины ряд параллельных близких штрихов, практически непрозрачных для света.

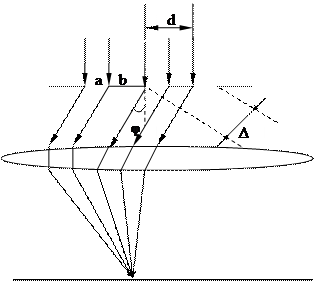Рис.5.2

На рис.5.2 дано увеличенное изображение поперечного сечения решетки: a – ширина щели, b – ширина непрозрачного промежутка. Величина, равная d=a+b называется периодом или постоянной решетки.

Пусть на решетку нормально падает плоская монохроматическая волна. Каждая щель даст на экране дифракционную картину, описанную ранее. Линза собирает лучи, идущие от всех щелей под углом j к главной оптической оси, в одну и ту же точку фокальной плоскости. Лучи, идущие под углом j=0 сходятся в одинаковой фазе, поэтому их амплитуды просто складываются. Лучи, идущие под углом j≠0, сходятся в ту или иную точку фокальной плоскости, пройдя различные пути, т.е. с разными фазами колебаний. Если на разности хода лучей Δ, идущих от соответствующих точек двух соседних щелей, укладывается целое число длин волн, то колебания от этих щелей взаимно усиливают друг друга. Благодаря этому возникают главные максимумы, удовлетворяющие условию

d sinφ = kλ (5.2)

k называется порядком спектра. Число порядков ограничено и определяется формулой

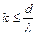(5. 3)

Если на решетку падает белый свет или любой другой свет сложного состава, то в результате дифракции произойдет разложение света в цветной спектр, т.к. условие (5.2) выполняется для каждой из длин волн λ в отдельности.

Описание установки.

Для изучения дифракционной картины и измерения углов дифракции служит гониометр. Принципиальная схема гониометра приведена на рис.5.3. Он состоит из металлической стойки, в верхней части которой вмонтирован горизонтально расположенный лимб 5, и нониуса, жестко связанного с коллиматором 4. Щель коллиматора, освещаемая источником света (ртутной лампой) 1, располагается в главном фокусе коллиматорной линзы 2. Пучок параллельных лучей, выходящих из этой линзы, падает на дифракционную решетку 6 и преобразуется ею в ряд параллельных пучков, идущих в направлении дифракционных максимумов.

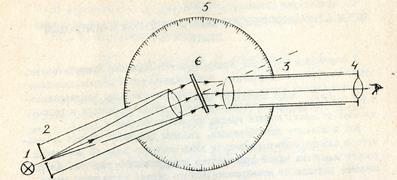
Рис.5.3.

Эти пучки попадают в объектив зрительной трубы 3 и после преломления сходятся в его фокальной плоскости. Наблюдаемая в окуляре трубы дифракционная картина представляет собой два ряда спектров, расположенных симметрично по отношению к центральному максимуму. Максимум имеет форму освещаемой щели.

При измерении гониометром углов дифракции следует иметь в виду, что цена деления на шкале лимба равна 0,5 градуса, а нониуса-1 минуте.