Биномиальное распределение
Описывает N независимых частиц или N независимых попыток с положительным, или отрицательным исходом. Положительный исход назовем случаем.
Если p – вероятностьпризнака у одной частицы, или вероятность одного случая, то вероятностьтого, чтоnлюбых частиц обладают этим признаком, или вероятность возникновения n случаев, равна
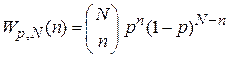 , (1.14)
, (1.14)
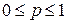 ;
; 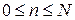 ;
;
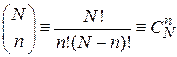 – биномиальный коэффициент.
– биномиальный коэффициент.
Выполняется
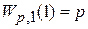 .
.
Распределение обосновал Якоб Бернулли в 1713 г.

Якоб Бернулли (1654–1705)
Доказательство:
Объект – идеальный газ из N тождественных частиц в объеме V.
Получим вероятность обнаружения n любых частиц в объеме 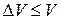 .
.
1. Вероятность найти определенную частицу в объеме DV согласно определению вероятности (1.4а)
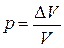 .
.
Вероятность найти определенную частицу вне объема DV
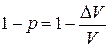 .
.
Эти несовместимые события образуют полный набор и удовлетворяют условию нормировки.
2. Вероятность найти n определенных частиц в объеме DV согласно теореме об умножении вероятностей независимых событий (1.4б)
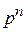 .
.
Вероятность найти (N – n) определенных частиц вне объема DV
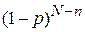 .
.
3. Вероятность найти одновременно n определенных частиц в объеме DV и (N – n) других частиц вне этого объема
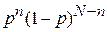 .
.
4. Взаимная перестановка тождественных частиц дает состояние, не отличимое от исходного. Число таких состояний равно числу сочетаний n частиц из общего числа N, т. е. равно 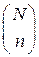 .
.
5. В результате вероятность найти n любых частиц в объеме DV и (N – n) любых других частиц вне DV
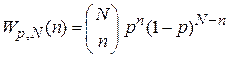 .
.
Условие нормировки
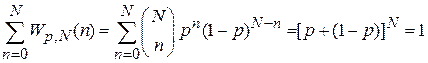 ,
,
использован бином Ньютона
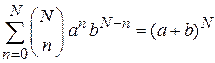 .
.

Исаак Ньютон (1642–1727)
Среднее число частиц в объеме DV
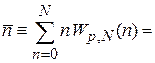
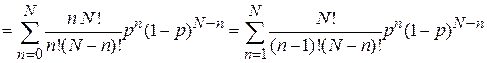 ,
,
где учтено
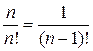 ;
;  .
.
Замена 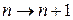 и бином Ньютона дают
и бином Ньютона дают
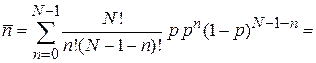
= 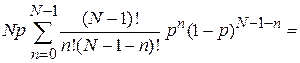
= 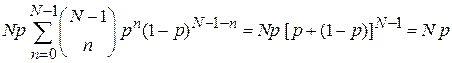 .
.
Результат
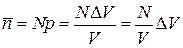 (1.15)
(1.15)
очевиден, поскольку 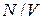 – средняя концентрация.
– средняя концентрация.
Из (1.15) вероятность признака у одного элемента
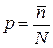 . (1.16)
. (1.16)
Из биномиального распределения получаем – если в некотором состоянии наблюдается в среднем 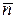 частиц, то вероятность наблюдения n частицравна
частиц, то вероятность наблюдения n частицравна
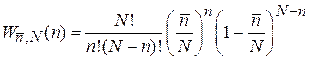 , (1.17)
, (1.17)
причем
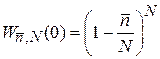 , (1.17а)
, (1.17а)
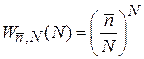 . (1.17б)
. (1.17б)
График распределения
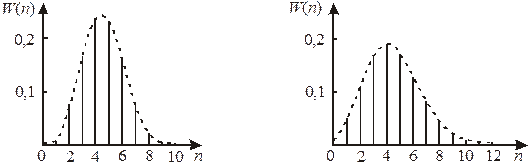
а б
Распределения биномиальное (а) и Пуассона (б) для N = 10, 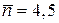 , р = 0,45
, р = 0,45
Распределение Пуассона
Считаем вероятность появления признака у одной частицы малой 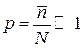 и общее число частиц большим
и общее число частиц большим 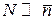 . Тогда, если признак имеют в среднем
. Тогда, если признак имеют в среднем 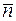 частиц, то его вероятность для n частиц
частиц, то его вероятность для n частиц
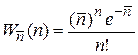 . (1.18)
. (1.18)
Результат получил из биномиального распределения Пуассон в 1837 г.

Симеон Дени Пуассон (1781–1840)
Доказательство:
Записываем биномиальное распределение (1.17)
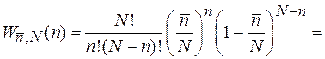
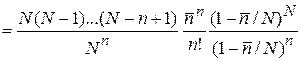 ,
,
где учтено
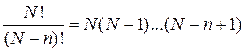 .
.
При 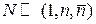 используем
используем
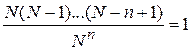 ,
,
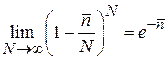 ,
,
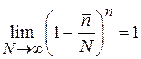 ,
,
и получаем (1.18).
Условие нормировки
Используем
N – велико, 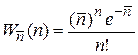 ,
, 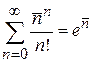 ,
,
получаем
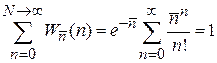 .
.
Частные и рекуррентные соотношения
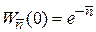 ,
,
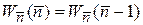 ,
,
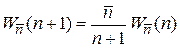 ,
,
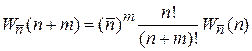 . (1.18а)
. (1.18а)
График распределения

а б
Распределения биномиальное (а) и Пуассона (б) для N = 10, 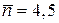 , р = 0,45
, р = 0,45
