Гипотеза Бекенштейна об энтропии
Серьезнее всего к аналогии между термодинамикой и механикой черных дыр
отнесся Яаков Бекенштейн, который был тогда аспирантом Джона Уилера . В то
время как все физическое сообщество заинтересованно изучало физику эле-
ментарных частиц (это были героические дни 1960-х и 1970-х годов, период
становления Стандартной модели), Уилер, в свободное от сочинения емких
замечаний время, с энтузиазмом продвигал область квантовой гравитации
(и общую теорию относительности в целом) . Влияние Уилера чувствовалось
не только посредством его идей — совместно с Брайсом Девиттом они впервые
обобщили уравнение Шрёдингера из квантовой механики для гравитационной
теории, но и через его учеников . Помимо Бекенштейна, под началом Уилера
успели получить степень кандидата наук (Ph .D .) немало ученых, которые се-
годня являются признанными лидерами в исследовании гравитации, включая
Кипа Торна, Чарльза Мизнера, Роберта Уолда и Уильяма Унру, не говоря уж
о Хью Эверетте, а также первом студенте Уилера, некоем Ричарде Фейнмане .
Итак, в начале 1970-х годов Принстон был плодовитой средой для исследо-
ваний черных дыр, и Бекенштейн находился в центре событий . В своей дис-
сертации он сделал простое, но исключительно эффектное предположение:
связь между механикой черных дыр и термодинамикой — это не просто ана-
логия . Это тождество . В частности, Бекенштейн использовал идеи из теории
передачи информации, доказывая, что площадь горизонта событий черной
дыры не просто похожа на энтропию, а в действительности и есть энтропия
черной дыры .10
На первый взгляд это предположение кажется несколько неправдоподобным .
Больцман уже рассказал нам, что такое энтропия: это мера количества микро-
скопических состояний системы, неразличимых с макроскопической точки
зрения . Казалось бы, выражение «у черных дыр нет волос» подразумевает, что
у большой черной дыры мало состояний, ведь она полностью характеризуется
значениями массы, заряда и углового момента . Однако здесь на сцену выходит 
Часть IV . Из кухни в Мультиленную
Бекенштейн и заявляет, что энтропия чер-
ной дыры астрофизических размеров оше-
ломительно велика .
Площадь горизонта событий должна
измеряться в каких-то единицах: акрах,
гектарах, квадратных сантиметрах — что
вам больше нравится . Бекенштейн утверж-
дал, что энтропия черной дыры примерно
равна площади горизонта событий, вы-
раженной в единицах планковской площади.
Рис . 12 .2 . Яаков Бекенштейн, ученый, Планковская длина, равная 10-33 сантиме-
впервые выдвинувший предположение
о том, что черные дыры обладают эн-
тропией
ную роль; планковская площадь — это всего лишь квадрат планковской длины .
Для черной дыры, масса которой сравнима с массой Солнца, площадь горизон-
та событий составляет около 1077 планковских площадей . Это большое число;
энтропия, равная 1077, — это больше, чем обычная энтропия всех звезд, газа
и пыли во всей галактике Млечный Путь .
Если не копать слишком глубоко, то найти способ, как справиться с оче-
видной несостыковкой «безволосой» идеи и бекенштейновского представ-
ления об энтропии, совсем нетрудно: можно считать, что классическая общая
теория относительности неверна и нам требуется квантовая гравитация для
описания громадного количества состояний, существование которых под-
разумевается энтропией черной дыры . Или, если уменьшить градус заум-
ности, классическая общая теория относительности схожа с термодинамикой,
а квантовая гравитация необходима для «статистически-механического»
понимания энтропии на микроскопическом уровне, в ситуациях, когда гра-
витация оказывает огромное влияние . Согласно предположению Бекенштей-
на, в действительности существует тьма тьмущая различных способов орга-
низации пространства—времени на микроскопическом квантовом уровне,
приводящих к созданию макроскопической классической черной дыры . Нам
остается только выяснить, что это за способы . Оказывается, проще сказать,
чем сделать; прошло более 35 лет, а мы до сих пор так до конца и не разо-
брались в природе этих микросостояний, подразумеваемых формулой энтро-
пии черной дыры . Мы думаем, что черная дыра похожа на контейнер с газом,
но нам неизвестно, что там за «атомы» внутри, — мы располагаем лишь
несколькими дразнящими намеками . 
|
|
|
|
Глава 12 . Черные дыры: конец времени
Тем не менее камень преткновения вовсе не в этом . Вспомните, что перво-
начально второе начало термодинамики было сформулировано Карно и Кла-
узиусом задолго до рождения Больцмана . Возможно, в вопросе исследования
квантовой гравитации прямо сейчас мы находимся на аналогичной стадии
прогресса . Вполне может оказаться, что, так же как температура и давление
в обычной термодинамике, свойства массы, заряда и углового момента в клас-
сической общей теории относительности — это простые макроскопические
наблюдаемые величины, не способные определить микросостояние пол-
ностью .
В представлении Бекенштейна черные дыры — это не какие-то странные
штуковины, держащиеся особняком от остальных физических объектов; это
термодинамические системы, такие же, как, например, контейнер с газом . Он
предложил «обобщенное второе начало термодинамики», представляющее
собой, по сути, обычное второе начало, но с добавлением энтропии черных
дыр . Мы можем взять контейнер с газом, обладающий определенной энтропи-
ей, бросить его в черную дыру и рассчитать общую энтропию до и после . Мы
увидим, что если согласиться с утверждением Бекенштейна о том, что энтропия
черной дыры пропорциональна площади горизонта событий, то энтропия
увеличится . Очевидно, что такой сценарий должен иметь важные следствия для
взаимосвязи энтропии с пространством—временем, стоящие того, чтобы
уделить им особое внимание .
Хокинговское излучение
Одновременно с деятельностью группы Уилера в Принстоне активная работа
над общей теорией относительности велась в начале 1970-х годов в Велико-
британии . В частности, Стивен Хокинг и Роджер Пенроуз изобретали и при-
меняли новые математические методы для изучения искривленного простран-
ства—времени . Результатом этих исследований стали знаменитые теоремы
о сингулярностях (когда гравитационная сила становится достаточно большой,
как в черных дырах или вблизи Большого взрыва, общая теория относитель-
ности предсказывает существование сингулярностей), а также сделанный
Хокингом вывод о том, что площадь горизонтов событий черных дыр никогда
не уменьшается .
Итак, Хокинг пристально следил за работой Бекенштейна, но она его не
слишком радовала . Прежде всего, если вы собираетесь принимать аналогию
между площадью горизонта событий и энтропией всерьез, то должны не менее
серьезно относиться и к прочим составляющим аналогии термодинамика/ 
Часть IV . Из кухни в Мультиленную
механика-черной-дыры . В частности, поверхностная гравитация черной дыры
(которая велика для небольших черных дыр с ничтожно малым угловым мо-
ментом и зарядом и довольно мала для больших черных дыр или черных дыр
со значительным спином или зарядом) должна быть пропорциональна ее тем-
пературе . Но это на первый взгляд кажется полнейшим абсурдом . Нагретые
до высокой температуры, объекты начинают испускать излучение — как рас-
плавленный металл или горящее пламя . Однако черные дыры не излучают; они
черные . «Так-то вот!» — наверняка думал Хокинг на другом берегу Атланти-
ческого океана .
Неутомимый путешественник, в 1973 году Хокинг посетил Советский Союз,
для того чтобы поговорить о черных дырах . В Москве в то время трудилась,
успешно соперничая с группами в Принстоне и Кембридже, группа экспертов
по относительности и космологии под руководством Якова Зельдовича . Зель-
дович и его коллега Александр Старобинский рассказали Хокингу о работе,
которую они проделали для того, чтобы понять процесс Пенроуза, — извле-
чение энергии из вращающейся черной дыры — в контексте квантовой меха-
ники . Согласно выводам московской группы, квантовая механика указывает,
что вращающаяся черная дыра должна сама спонтанно испускать излучение
и терять энергию; нет никакой необходимости в том, чтобы суперпродвинутая
цивилизация бросалась в нее какими-то вещами .
Хокинг был заинтригован, но его не вполне убедили конкретные доводы,
приведенные Зельдовичем и Старобинским .11 И он поставил целью само-
стоятельно разобраться в следствиях, к которым приводит квантовая меха-
ника в контексте черных дыр . Это не самая простая задача . «Квантовая
механика» представляет собой очень обобщенную идею: пространство со-
стояний включает волновые функции, а не положения и импульсы, и невоз-
можно напрямую измерить волновую функцию, не оказав на нее существен-
ного влияния . В рамках этого подхода можно рассматривать самые разные
типы квантовых систем — от отдельных частиц до наборов суперструн .
Основатели квантовой механики вполне предсказуемо фокусировались на
относительно простых системах, состоящих из небольшого числа атомов,
двигающихся друг относительно друга довольно медленно . Именно такие
системы предлагаются для изучения большинству студентов-физиков при
первом знакомстве с квантовой механикой .
Когда частицы набирают высокую энергию и начинают перемещаться со
скоростью, близкой к скорости света, мы больше не можем игнорировать уро-
ки теории относительности . Как минимум, энергия двух частиц, которые
сталкиваются друг с другом, может быть настолько высокой, что они рождают 
Глава 12 . Черные дыры: конец времени
несколько новых частиц посредством чуда соотношения E = mc2 . Благодаря
десятилетиям напряженной работы физиков-теоретиков надлежащий форма-
лизм, примиряющий квантовую механику со специальной теорией относитель-
ности, был получен в форме квантовой теории поля .
Основная идея квантовой теории поля проста: мир сделан из полей,
и когда мы наблюдаем волновые функции этих полей, мы видим частицы .
В отличие от частицы, которая существует в какой-то конкретной точке, поле
распространяется на все пространство целиком; электрическое поле, маг-
нитное поле, гравитационное поле — все это давно знакомые всем нам при-
меры . В каждой точке пространства каждое существующее поле обладает
определенным значением (которое также может быть нулевым) . Согласно
квантовой теории поля, полем является абсолютно все: есть поле электронов,
различные типы кварковых полей и т . д . Но когда мы смотрим на поле, мы
видим частицы . Например, изучая электрическое и магнитное поля, мы видим
фотоны — частицы, относящиеся к электромагнетизму . Слабо осциллирую-
щее электромагнитное поле обнаруживается в форме небольшого числа
фотонов; сильно осциллирующее электромагнитное поле обнаруживается
в виде большого числа фотонов .12
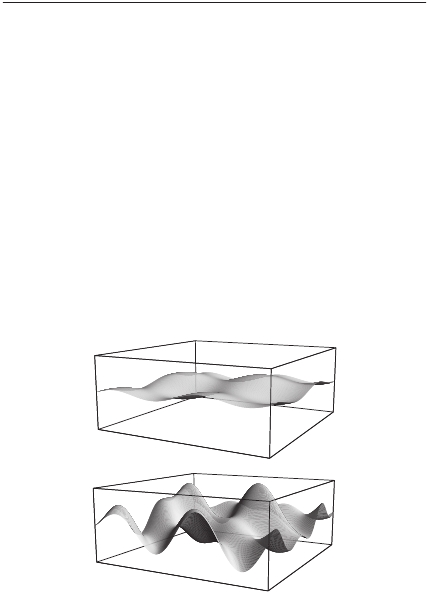
Рис . 12 .3 . В каждой точке пространства у полей есть значения . Наблюдая квантовое поле,
мы видим не само поле, а набор частиц . Слегка осциллирующее поле, такое как показанное
на верхнем рисунке, соответствует малому числу частиц; сильно вибрирующее поле, изо-
браженное на нижнем рисунке, соответствуют большому числу частиц
|
Часть IV . Из кухни в Мультиленную
Квантовая теория поля примиряет квантовую механику со специальной
теорией относительности . Это совсем не то, что «квантовая гравитация»,
которая, в свою очередь, примиряет квантовую механику с общей теорией от-
носительности, теорией гравитации и искривленного пространства—времени .
В квантовой теории поля мы считаем, что пространство—время само по себе
классическое, искривлено оно или нет; поля подчиняются правилам квантовой
механики, тогда как пространство—время всего лишь играет роль жестко за-
крепленного, неизменного фона . В случае полнофункциональной квантовой
гравитации, наоборот, мы полагаем, что даже у пространства—времени есть
волновая функция и оно полностью квантово-механическое . Работа Хокинга
была выполнена в контексте квантовой теории поля на фиксированном фоне
искривленного пространства—времени .
Теория поля никогда не была специализацией Хокинга . Несмотря на то что
она, как и общая теория относительности, в общественном сознании воспри-
нимается как еще одна «современная физическая теория со звучным названи-
ем, непостижимая для обычного человека», эти две области сильно отличают-
ся друг от друга, и эксперт в одной из них может слабо разбираться в другой .
Так что Хокинг взялся за учебу . Сэр Мартин Рис, один из ведущих мировых
астрофизиков-теоретиков, служащий в настоящее время королевским астро-
номом Британии, был в то время молодым ученым из Кембриджа . Как и Хокинг,
он получил кандидатскую степень несколькими годами ранее под руководством
Денниса Сиама . К этому времени тело Хокинга было уже сильно деформиро-
вано из-за болезни; когда ему требовался учебник по квантовой теории поля,
Рису приходилось открывать книгу и держать ее перед коллегой . Хокинг мог
часами безмолвно изучать научные тексты, и Рис задавался вопросом, не пре-
вращается ли болезнь в слишком тяжелый груз для Хокинга .13
Но ничего подобного . В действительности Хокинг применял формализм тео-
рии поля к вопросу излучения черных дыр . Он надеялся вывести формулу, которая
позволит воспроизвести результат Зельдовича и Старобинского для вращающих-
ся черных дыр, но все время натыкался на что-то совершенно невероятное: соз-
давалось впечатление, что, согласно квантовой теории поля, даже из невращаю-
щихся черных дыр должно исходить излучение . То есть они должны излучать
точно так же, как система в термодинамическом равновесии при какой-то фикси-
рованной температуре, пропорциональной поверхностной гравитации, — в точ-
ности как предписывает аналогия между черными дырами и термодинамикой .
К своему удивлению, Хокинг доказал правоту Бекенштейна . Черные дыры
действительно ведут себя как обычные термодинамические объекты . Это
означает, помимо прочего, что энтропия черной дыры на самом деле пропор- 
Глава 12 . Черные дыры: конец времени
циональна площади ее горизонта событий; оказалось, что связь между этими
двумя величинами — вовсе не простое забавное совпадение . Более того, рас-
четы Хокинга (в отличие от заявления Бекенштейна) позволили ему установить
точный коэффициент пропорциональности: ¼ . Таким образом, если Lp —
планковская длина, а L2p — планковская площадь, то энтропия черной дыры
равна ¼ площади ее горизонта, измеренного в единицах планковской площади:
.
Нижний индекс BH можно читать как Black Hole — «черная дыра» по-
английски либо как Bekenstein—Hawking (Бекенштейн—Хокинг) — как вам
больше нравится . Эта формула — самый важный ориентир, который у нас есть
в деле примирения гравитации и квантовой механики .14 И если мы хотим по-
нять, почему сразу после Большого взрыва энтропия была очень мала, то нам
необходимо разложить по полочкам наши знания об энтропии и гравитации,
так что логично начать именно с них .
Испарение
Для того чтобы полностью разобраться, каким образом Хокинг пришел к это-
му потрясающему результату — пониманию того, что черные дыры излучают, —
необходимо провести тщательный математический анализ поведения квантовых
полей в искривленном пространстве . Однако существует также популярное
объяснение «на пальцах», и оно содержит достаточно ценной истины, чтобы
на него могли опираться все люди мира, включая Хокинга . Так почему бы нам
не последовать их примеру?
Основная мысль состоит в том, что квантовая теория поля подразумевает
существование «виртуальных частиц» в дополнение к старым добрым реальным
частицам . Мы мимоходом упомянули об этой идее в главе 3, когда обсуждали
энергию вакуума . Казалось бы, самую низкую энергию квантовое поле должно
иметь в состоянии, когда оно абсолютно постоянно, то есть просто существует
в неизменном виде, не меняясь от точки к точке или от одного момента времени
к другому . Если бы речь шла о классическом поле, все так и было бы, но как
в квантовой механике невозможно привязать частицу к одному конкретному
положению, так и в квантовой теории поля нельзя привязать поле к одной кон-
кретной конфигурации . Значение квантового поля всегда будет содержать какие-
то неопределенности и нечеткость — это неотъемлемое его свойство . Это
присущее квантовым полям дрожание можно относить на счет появления 





|
|
|
|
Часть IV . Из кухни в Мультиленную
и исчезновения частиц — по одной частице и одной античастице за раз, причем
происходит это так стремительно, что мы просто не успеваем их заметить . Такие
виртуальные частицы невозможно засечь напрямую; если мы видим частицу, то
точно знаем, что это реальная, а не виртуальная частица . Однако виртуальные
частицы могут взаимодействовать с реальными (не виртуальными), едва ощути-
мо изменяя их свойства, и это воздействие можно пронаблюдать и изучить
в мельчайших деталях . Виртуальные частицы действительно существуют .
Одним из важнейших выводов Хокинга было то, что гравитационное поле
черной дыры способно превращать виртуальные частицы в реальные . Обычно
виртуальные частицы появляются парами: одна частица и одна античастица .15
Они возникают, существуют на протяжении кратчайшего времени, а затем
аннигилируют, пока никто не заметил . Но благодаря наличию горизонта со-
бытий черная дыра все меняет . Когда пара из виртуальной частицы и антича-
стицы образуется очень близко к горизонту, одна из частиц может упасть под
горизонт, и, очевидно, у нее не останется других вариантов, кроме как про-
должать падение в сингулярность . Тем временем другая частица сможет убежать
на бесконечность . Горизонт событий разорвал виртуальную пару, поглотив
одну из частиц . А убежавшая частица стала частью хокинговского излучения .
Теперь на сцену выходит важнейшее свойство виртуальных частиц: их
энергия может быть вообще какой угодно . Общая энергия пары из виртуальной
частицы и античастицы в точности равна нулю — это необходимое условие,
так как они должны уметь появляться из вакуума и растворяться в нем . Энергия
реальных частиц равна произведению массы на квадрат скорости света, когда
частица находится в покое, а с началом движения частицы возрастает; следова-
тельно, энергия никогда не может быть отрицательной . Таким образом, если
у реальной частицы, убежавшей от черной дыры, положительная энергия,
а общая энергия исходной виртуальной пары была нулевой, значит, у частицы,
упавшей в черную дыру, энергия отрицательная. И когда эта частица падает,
общая масса черной дыры уменьшается .
В конце концов, если она не получит какую-то дополнительную энергию
из других источников, черная дыра полностью испарится . Оказывается, черные
дыры нельзя считать областями, где время обрывается раз и навсегда; это объ-
екты, которые успевают просуществовать в течение какого-то периода време-
ни, прежде чем окончательно исчезнуть . В каком-то смысле хокинговское из-
лучение сделало черные дыры намного более приземленными, чем они казались
в классической общей теории относительности .
Хокинговское излучение обладает интересным свойством: чем меньше
черная дыра, тем она горячее. Температура пропорциональна поверхностной 
Глава 12 . Черные дыры: конец времени
Рис . 12 .4 . Хокинговское излучение . В квантовой теории поля виртуальные частицы и анти-
частицы постоянно образуются из вакуума и исчезают в вакууме . Однако поблизости от
черной дыры одна из пары частиц может провалиться под горизонт событий, а другая —
убежать во внешний мир в форме хокинговского излучения
гравитации, которая тем больше, чем менее массивную черную дыру мы рас-
сматриваем . У тех типов астрофизических черных дыр, о которых мы говорим
в этой главе (с массой, равной массе Солнца или намного ее превышающей),
очень низкие хокинговские температуры; во Вселенной в ее текущем состоянии
такие черные дыры вообще не испаряются, так как забирают намного больше
энергии у окружающих объектов, чем теряют посредством хокинговского из-
лучения . Ситуация не поменялась бы, даже если бы единственным внешним
источником излучения был космический микроволновый фон с температурой
около 3 кельвинов . Для того чтобы черная дыра имела температуру выше, чем
сегодняшняя температура космического микроволнового фона, ее масса долж-
на составлять менее 1014 килограммов — приблизительно столько весит гора
Эверест, а это намного меньше, чем у любой известной нам черной дыры .16
Разумеется, фоновое микроволновое излучение становится все холоднее по
мере расширения Вселенной, так что если подождать достаточно долго, черные
дыры станут теплее окружающей Вселенной и начнут терять массу . В ходе
этого процесса они будут нагреваться и терять массу еще быстрее; процесс
выйдет из-под контроля, и как только черные дыры съежатся до критического
размера, их быстрый конец наступит в форме эффектных взрывов .
К сожалению, численная величина ожидаемого эффекта не позволяет
Стивену Хокингу получить Нобелевскую премию за предсказание существо- 
|

Часть IV . Из кухни в Мультиленную
вания излучения из черных дыр . Если говорить о типах черных дыр, известных
нам сегодня, то излучение из них слишком ничтожно, чтобы его можно было
засечь в обсерватории . Возможно, нам повезет, и когда-нибудь мы обнаружим
чрезвычайно маленькую черную дыру, испускающую высокоэнергетиче-
ское излучение, но шансы невелики .17 А Нобелевская премия вручается за
эффекты, которые можно реально пронаблюдать уже сейчас, а не просто за
отличные идеи . И все же авторы отличных идей не остаются без вознаграж-
дения .
Потеря информации?
Тот факт, что черные дыры испаряются, поднимает важный вопрос: что про-
исходит с информацией, которая участвовала в образовании черной дыры? Мы
упоминали о сбивающем с толку следствии принципа «отсутствия волос»
у черных дыр в классической общей теории относительности: независимо от
того, из чего была образована черная дыра, после завершения процесса ее
формирования единственными ее характеристиками являются масса, заряд
и угловой момент . В предыдущих главах мы много говорили о том, что по мере
развития Вселенной, от одного момента времени к другому, законы физики
сохраняют информацию, необходимую для описания состояния . На первый
взгляд кажется, что черные дыры уничтожают эту информацию .
Представьте себе, что вы, окончательно расстроившись из-за неспособности
современной физики предоставить достойное объяснение стрелы времени,
швыряете эту книгу в огонь . Позднее вас начинает глодать мысль о том, что
этот импульсивный поступок был большой ошибкой, и вы хотите получить
книгу обратно . К сожалению, она уже сгорела дотла . Однако законы физики
говорят нам, что вся информация, содержащаяся в книге, в принципе, осталась
доступной, как бы ни было трудно ее восстановить на практике . Горящая кни-
га эволюционировала в одну конкретную конфигурацию пепла, света и тепла .
Если бы мы могли точно описать полное микросостояние Вселенной после
того, как огонь погас, мы, теоретически, могли бы прокрутить стрелки часов
в обратную сторону и выяснить, что за книга тогда сгорела: эта, которую вы
читаете, или, например, «Краткая история времени» (демону Лапласа было
бы известно, какая именно) . Конечно же, все это лишь теоретические измыш-
ления, потому что по ходу дела энтропия также значительно увеличится, но,
в принципе, это вполне реальный сценарий .
Если же вместо того, чтобы швырять книгу в огонь, вы забросите ее в черную
дыру, история изменится . Согласно классической общей теории относитель- 
Глава 12 . Черные дыры: конец времени
Рис . 12 .5 . Информация (например, книга) падает в черную дыру и должна выйти наружу
в форме хокинговского излучения . Но как она может быть одновременно в двух местах?
ности, восстановить информацию будет невозможно; книга упала в черную
дыру, и мы ничего не можем сделать, кроме как измерить массу, заряд и угловой
момент черной дыры . Другие характеристики нам недоступны . Единственное
наше утешение — надежда, что эта информация где-то все же сохранилась,
просто нам теперь до нее не добраться .
Однако ситуация предстает в совершенно ином свете, как только в игру
вступает хокинговское излучение . Теперь черная дыра не живет вечно; если
мы терпеливо подождем, она полностью испарится . И если информация не
теряется, то мы должны оказаться в том же случае, как и в примере с огнем; то
есть, в принципе, быть способными восстановить содержимое книги, изучая
свойства выходящего излучения .
Проблема с подобными ожиданиями возникает, когда мы начинаем анали-
зировать, каким образом виртуальные частицы порождают хокинговское из-
лучение вблизи горизонта событий черной дыры . Исходя из того, что изобра-
жено на рис . 12 .5, можно подумать, что книга проваливается сквозь горизонт
и попадает в сингулярность (или туда, что заменяет сингулярность в теории
квантовой гравитации), забирая с собой всю информацию, содержащуюся на
страницах . В то же время излучение, которое предположительно переносит ту
же информацию, уже покинуло черную дыру . Как одна и та же информация
может быть одновременно в двух местах?18 Расчеты Хокинга показывают, что
выходящее излучение совершенно одинаково для всех типов черных дыр, не-
зависимо от того, из чего они сделаны . Таким образом, получается, что инфор- 
|
Часть IV . Из кухни в Мультиленную
мация попросту уничтожается? Если вспомнить наши предыдущие примеры
с шахматными досками, то это аналогично существованию определенного рода
пятна, которое случайным образом порождает либо серые, либо белые квадра-
ты вне зависимости от предыдущего состояния .
Эта загадка известна как «парадокс о потере информации в черных дырах» .
Поскольку экспериментальную информацию о квантовой гравитации очень
сложно получить напрямую, размышления о том, как же все-таки разрешить
этот парадокс, в последние несколько десятилетий непрерывно занимали умы
множества физиков-теоретиков . Физическое сообщество раскололось на две
части . Физики, которые, грубо говоря, долго занимались общей теорией от-
носительности (включая Стивена Хокинга), склонялись к тому, что информация
действительно теряется и что испарение черной дыры — это пример наруше-
ния привычных правил квантовой механики . В то же время ученые, занимав-
шиеся физикой элементарных частиц и квантовой теорией поля, скорее были
готовы поверить в то, что нам необходимо лучше разобраться в вопросе ис-
парения черных дыр, и тогда мы увидим, что информация все же каким-то об-
разом сохраняется .
В 1997 году Хокинг и его коллега Кип Торн (оба из лагеря общей теории
относительности) заключили пари с Джоном Прескиллом, физиком-теорети-
ком, занимающимся изучением элементарных частиц в Калтехе . Вот текст
этого договора:
Исходя из того что Стивен Хокинг и Кип Торн твердо уверены, что инфор-
мация, поглощаемая черной дырой, навсегда скрывается из внешней Вселенной
и никогда, даже после испарения черной дыры, не может быть обнаружена
повторно и полностью исчезает, а также принимая во внимание, что Джон
Прескилл твердо уверен, что механизм выхода информации при испарении
черной дыры должен быть и будет обнаружен в правильной теории квантовой
гравитации,
Прескилл предлагает, а Хокинг и Торн принимают предложение заключить
пари о следующем:
Когда чистое квантовое начальное состояние претерпевает гравитационный
коллапс, формируя черную дыру, конечное состояние по завершении испарения
черной дыры всегда будет являться чистым квантовым состоянием.
Проигравший (проигравшие) наградит победителя (победителей) энцикло-
педией по выбору победителя, откуда тот может извлекать информацию по
своему желанию.
Стивен У. Хокинг, Кип С. Торн, Джон П. Прескилл
Пасадена, Калифорния, 6 февраля 1997 г. 
Глава 12 . Черные дыры: конец времени
В 2004 году Хокинг совершил поступок, о котором кричали заголовки всех
газет: он признал свое поражение, согласившись, что при испарении черной
дыры информация действительно сохраняется . Интересно также, что Торн со
своим поражением так и не согласился (по состоянию на момент написания
этой книги); более того, Прескилл с большой неохотой принял свой выигрыш
(энциклопедия Total Baseball: The Ultimate Baseball Encyclopedia, восьмое издание),
так как считал, что вопрос пока что еще не решен до конца .19
Что же убедило Хокинга, на протяжении тридцати лет утверждавшего, что
информация в черных дырах теряется, в том, что в действительности она со-
храняется? Ответ основывается на нескольких важных идеях, касающихся
пространства—времени и энтропии, поэтому для начала нам необходимо
познакомиться с основами .