Уравнение Шредингера для атома водорода

Решение уравнения Шрёдингера для водородного атома использует факт, что кулоновский потенциал является изотропным, то есть не зависит от направления в пространстве, другими словами, обладает сферической симметрией.

Уравнение Шрёдингера запишется следующим образом:

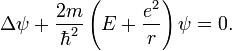
Здесь ψ — волновая функция электрона в системе отсчёта протона, m — масса электрона, 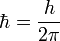— постоянная Планка, E — полная энергия электрона, 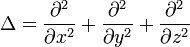— оператор Лапласа. Так как потенциальная функция зависит от r, а не от координат по отдельности, удобно будет записать лапласиан в сферической системе координат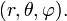

В полярных координатах уравнение, которому должна удовлетворять функция ψ(r, θ, φ), принимает вид

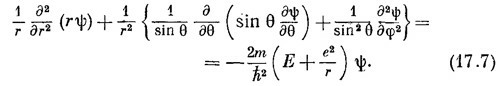Квантовые числа, их физический смысл

Квантовое число в квантовой механике — численное значение какой-либо квантованной переменной микроскопического объекта (элементарной частицы, ядра, атома и т. д.), характеризующее состояние частицы. Задание квантовых чисел полностью характеризует состояние частицы.

Некоторые квантовые числа связаны с движением в пространстве и характеризуют пространственное распределение волновой функции частицы. Это, например, радиальное (главное) ( 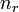), орбитальное ( 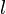) и магнитное ( 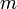) квантовые числа электрона в атоме, которые определяются как число узлов радиальной волновой функции, значение орбитального углового момента и его проекция на заданную ось, соответственно.

Некоторые другие квантовые числа никак не связаны с перемещением в обычном пространстве, а отражают «внутреннее» состояние частицы. К таким квантовым числам относится спин и его проекция. В ядерной физике вводится также изоспин, а в физике элементарных частиц появляется цвет, очарование, прелесть и истинность.

Собственные (спиновый) механический и магнитный момент электрона

Спиновый механический момент импульса электрона:

Спиновый магнитный момент электрона:

– это гиромагнитное (магнито – механическое) отношение орбитальных моментов электрона

Опыт Штерна и Герлаха

Опыт состоял в следующем: пучок атомов серебра пропускали через сильно неоднородное магнитное поле, создаваемое мощным постоянныммагнитом. При прохождении атомов через это поле, в силу обладания ими магнитных моментов, на них действовала зависящая от проекции спина на направление магнитного поля сила, отклонявшая летящие между магнитами атомы от их первоначального направления движения. Причём, если предположить, что магнитные моменты атомов ориентированы хаотично (непрерывно), то тогда на расположенной далее по направлению движения атомов пластинке должна была проявиться размытая полоса. Однако вместо этого на пластинке образовались две достаточно чёткие узкие полосы, что свидетельствовало в пользу того, что магнитные моменты атомов вдоль выделенного направления принимали лишь два определённых значения, что подтверждало предположение квантово-механической теории о квантовании магнитного момента атомов.

Идея опытов Штерна – Герлаха состояла в определении силы, действующей на атом элементов I группы (Ag, Li) в неоднородном внешнем магнитном поле. Она может быть вычислена по формуле ,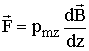
где 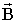– индукция магнитного поля, неоднородного по оси Z; 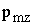– проекция магнитного момента атома на направление магнитного поля.