Раздел 2. квантование физических величин.

РАЗДЕЛ 1. ЭЛЕМЕНТЫ АТОМНОЙ ФИЗИКИ И КВАНТОВОЙ МЕХАНИКИ

ТЕМЫ

Тема 1. Волновые свойства микрочастиц.

Гипотеза де Бройля. Опыты Девиссона и Джермера. Дифракция электронов. Неприменимость понятия траектории к микрочастицам.

Л. 1: § 4.18; Л. 2: § 13.45.

Тема 2. Соотношения неопределенностей Гейзенберга.

Прохождение электронов через две щели. Соотношения неопределенностей. Прохождение частицы через щель. Оценка энергии нулевых колебаний гармонического осциллятора.

Л. 1: § 4.20; Л. 2: § 13.46.

Тема 3. Уравнение Шредингера.

Задание состояния частицы в квантовой физике: пси-функция, ее физический смысл как амплитуды вероятности. Нормировка. Стандартные условия. Суперпозиция в квантовой физике. Уравнение Шредингера (временное и стационарное). Стационарные состояния.

Л. 1: § 4.21; Л. 2: § 13.47.

Тема 4. Прохождение частиц через потенциальный барьер.

Задачи на применение уравнения Шредингера. Частицы в одномерной яме с абсолютно непроницаемыми стенками. Квантование энергии. Гармонический осциллятор (результаты решения). Туннельный эффект.

Л. 1: §4.26; Л. 2: § 4.27.

Литература [3, с.50 - 69]

МЕТОДИЧЕСКИЕ УКАЗАНИЯ.

Темы данного раздела посвящены экспериментальному обоснованию волновых свойств микрочастиц и корпускулярных свойств волны. Все экспериментальные факты подтверждают корпускулярно - волновой дуализм микрочастиц. Особое внимание надо обратить на соотношение неопределенностей, указывающее на отсутствие траекторий у микрочастиц, и на не применимость классических понятий в квантовой механике. Хорошей иллюстрацией этому служат решение уравнений Шредингера при прохождении частиц через потенциальный барьер, а также рассмотрение свойств микрочастицы, находящейся в потенциальной яме.

ОСНОВНЫЕ ФОРМУЛЫ.

Длина волны де Бройля: l = h/р = hc/(βЕ),

где p – импульс частицы, β = v/c.

Импульс частицы и его связь с кинетической энергией Т:

1. p = m₀v; p = (нерелятивистская);

2. p = mv = m₀v / 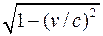; p = 1/c ,

р = βЕ/с

3. E² = p²c²+ m₀²c⁴, Т = mc²- m₀c²,

где m₀ - масса покоя частицы; m - релятивистская масса;

v - скорость частицы; c - скорость света в вакууме;

E₀ - энергия покоя частицы ( Е₀ = m₀c²), Е – полная энергия частицы ( Е = mc²).

Соотношение неопределенностей:

1. Dp_xDx ≥ h/4π (для координаты и импульса);

где Dp_x – неопределенность проекции импульса на ось x;

Dx - неопределенность координаты;

2. DEDt ≥ h/4π (для энергии и времени),

где DЕ - неопределенность энергии;

Dt - время жизни квантовой системы в данном энергетическом состоянии.

Одномерное уравнение Шредингера для стационарных состояний

(E – U)y(x) = 0,

где y(x) – волновая функция, описывающая состояние частицы;

m - масса частицы; E - полная энергия;

U = U(x) - потенциальная энергия частицы.

dw(x) = êψ(x)ï²dx ,

где dw(x) – вероятность того, что частица может быть обнаружена вблизи точки с координатой x на участке dx.

Вероятность обнаружения частицы в интервале от X₁ до X₂ :

.

Решение уравнения Шредингера для одномерного, бесконечно глубокого, прямоугольного потенциального ящика:

y_n(x) = 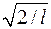sin (собственная нормированная волновая функция):

E_n = 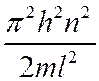; (собственные значения энергии),

где n-квантовое число (n = 1, 2, 3, …);

l - ширина ящика (потенциальной ямы).

В областях X > l и X <0 при U(0, l) = µ имеем ψ (x) = 0.

РАЗДЕЛ 2. КВАНТОВАНИЕ ФИЗИЧЕСКИХ ВЕЛИЧИН.

ТЕМЫ