Алгоритмы обработки данных устройствами, позволяющими обнаружить и исправить ошибки.

Обнаружение ошибок в технике связи — действие, направленное на контроль целостно­сти данных при записи/воспроизведении информации или при её передаче по линиям связи. Исправление ошибок (коррекция ошибок) — процедура восстановления информации после чтения её из устройства хранения или канала связи.

Для обнаружения ошибок используют коды обнаружения ошибок, для исправления — корректирующие коды (коды, исправляющие ошибки, коды с коррекцией ошибок, помехоустойчивые коды).

Способы борьбы с ошибками

В процессе хранения данных и передачи информации по сетям связи неизбежно возникают ошибки. Контроль целостности данных и исправление ошибок — важные задачи на многих уров­нях работы с информацией (в частности, физическом, канальном, транспортном уровнях модели OSI).

В системах связи возможны несколько стратегий борьбы с ошибками:

§ обнаружение ошибок в блоках данных и автоматический запрос повторной передачи повреждённых блоков — этот подход применяется в основном на канальном и транспортном уровнях;

§ обнаружение ошибок в блоках данных и отбрасывание повреждённых блоков — такой под­ход иногда применяется в системах потокового мультимедиа, где важна задержка передачи и нет времени на повторную передачу;

§ исправление ошибок (forward error correction) применяется на физическом уровне.

§ Коды обнаружения и исправления ошибок

Корректирующие коды — коды, служащие для обнаружения или исправления ошибок, возни­кающих при передаче информации под влиянием помех, а также при её хранении.

Для этого при записи (передаче) в полезные данные добавляют специальным образом структури­рованную избыточную информацию (контрольное число), а при чтении (приёме) её используют для того, чтобы обнаружить или исправить ошибки. Естественно, что число ошибок, которое можно исправить, ограничено и зависит от конкретного применяемого кода.

С кодами, исправляющими ошибки, тесно связаны коды обнаружения ошибок. В отличие от пер­вых, последние могут только установить факт наличия ошибки в переданных данных, но не ис­править её.

В действительности, используемые коды обнаружения ошибок принадлежат к тем же классам ко­дов, что и коды, исправляющие ошибки. Фактически, любой код, исправляющий ошибки, может быть также использован для обнаружения ошибок (при этом он будет способен обнаружить боль­шее число ошибок, чем был способен исправить).

По способу работы с данными коды, исправляющие ошибки делятся на блоковые, делящие ин­формацию на фрагменты постоянной длины и обрабатывающие каждый из них в отдельности, и свёрточные, работающие с данными как с непрерывным потоком.

Блоковые коды

Пусть кодируемая информация делится на фрагменты длиной k бит, которые преобразуются в кодовые слова длиной n бит. Тогда соответствующий блоковый код обычно обозначают 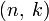. При этом число 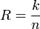называется скоростью кода.

Если исходные k бит код оставляет неизменными, и добавляет n − k проверочных, такой код назы­вается систематическим, иначе несистематическим.

Задать блоковый код можно по-разному, в том числе таблицей, где каждой совокупности из k информационных бит сопоставляется n бит кодового слова. Однако, хороший код должен удовлетворять, как минимум, следующим критериям:

§ способность исправлять как можно большее число ошибок,

§ как можно меньшая избыточность,

§ простота кодирования и декодирования.

Практически все используемые коды являются линейными. Это связано с тем, что нелинейные коды значительно сложнее исследовать, и для них трудно обеспечить приемлемую лёгкость коди­рования и декодирования.

Линейные коды общего вида

Линейный блоковый код — такой код, что множество его кодовых слов образует k-мерное линей­ное подпространство (назовём его C) в n-мерном линейном простран­стве,изоморфное пространству k-битных векторов.

Линейные циклические коды

Несмотря на то, что декодирование линейных кодов уже значительно проще декодирования боль­шинства нелинейных, для большинства кодов этот процесс всё ещё достаточно сло­жен. Циклические коды, кроме более простого декодирования, обладают и другими важными свойст­вами.

Циклическим кодом является линейный код, обладающий следующим свойством: если 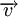явля­ется кодовым словом, то его циклическая перестановка также является кодовым словом.

Слова циклического кода удобно представлять в виде многочленов. Например, кодовое слово 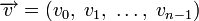представляется в виде поли­нома 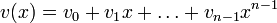. При этом циклический сдвиг кодового слова эквива­лентен умножению многочлена на x по модулю xⁿ − 1.

Коды CRC

Коды CRC (cyclic redundancy check — циклическая избыточная проверка) явля­ются систематическими кодами, предназначенными не для исправления ошибок, а для их обна­ружения. Они используют способ систематического кодирования, изложенный выше: «контроль­ная сумма» вычисляется путем деления x^{n − k}u(x) на g(x). Ввиду того, что исправление ошибок не требуется, проверка правильности передачи может производиться точно так же.

Таким образом, вид полинома g(x) задаёт конкретный код CRC. Примеры наиболее популярных полиномов:

название кода	степень	полином
CRC-12		x12 + x11 + x3 + x2 + x + 1
CRC-16		x16 + x15 + x2 + 1
CRC-CCITT		x16 + x12 + x5 + 1
CRC-32		x32 + x26 + x23 + x22 + x16 + x12 + x11 + x10 + x8 + x7 + x5 + x4 + x2 + x + 1

Коды БЧХ

Коды Боуза — Чоудхури — Хоквингема (БЧХ) являются подклассом циклических кодов. Их отличи­тельное свойство — возможность построения кода БЧХ с минимальным расстоянием не меньше заданного. Это важно, потому что, вообще говоря, определение минимального расстояния кода есть очень сложная задача.

Математически полинома g(x) на множители в поле Галуа.