Критерии качества и правила приема дискретных сооб-й. Отношение правдоподобия

Критерий Котельникова или критерий идеального наблюдателя, согласно которому качество демодулятора оценивают безусловной (средней) вероятностью правильного приёма символа. Пусть на вход демодулятора в течение отрезка [0, T] приходит некоторый элемент сигнала z(t). Предположим, что демодулятор принимает при этом решение, что передан символ b_i,т.е. выдаёт оценку 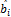. Вероятность того, что это решение правильно, очевидно, равна условной вероятности P(b_i|z(t)) того, что действительно передавался символ b_i, при условии прихода реализации элемента сигнала z(t). Её называют апостериорной вероятностью символа b_i (т.е. вероятностью, определённой после опыта, заключающегося в наблюдении и анализе сигнала z(t)).Критерий идеального наблюдателя обеспечивается решающей схемой, построенной по правилу максимума апостериорной вероятности — решение , принимается в том случае, если выполняется система из m-1 неравенств: 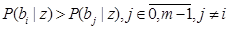(1)

Для двоичной системы сигналов упомянутое правило сводится к проверке неравенства P(1|z)>P(0|z) (2). При выполнении неравенства (2) регистрируется символ 1, в противном случае — 0. Другая форма записи решения по критерию Котельникова: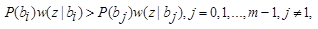

Приёмник, реализующий этот алгоритм , называют приёмником Котельникова. Для двоичной системы правило сводится к проверке неравенства P(1)ω(z׀1)>P(0)ω(z׀0), при выполнении которого регистрируется символ 1, а при невыполнении — 0. Для построения решающей схемы по правилу критерия идеального наблюдателя необходимо знать априорные вероятности символов P(b_i), а также свойства модулятора и канала, определяющие условные плотности w(z|b_i),j - функции правдоподобия. Критерий Котельникова можно записать иначе. Решение о том, что передавался символ b_i должно приниматься, если для всех j≠ i выполняются т — 1 неравенств

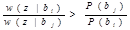(2)

Отношение в левой части этого неравенства называется Отношением правдоподобия двух гипотез: о том, что передавался символ b_i, и о том, что передавался символ b_j. Его обозначают Λ_ij, В случае, когда все m символов передаются равновероятно, т.е. P(b_i)=1/m, правило (2) упрощается: Λ_ij>1, i 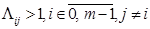(3)

Иногда вводят в рассмотрение помимо т гипотез о передаче символов 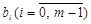ещё дополнительную ("шумовую") гипотезу о том, что никакой сигнал не передавался, т.е. z(t)=n(t) — чистая помеха. Отношение правдоподобия 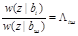обычно обозначают просто Λ_i. Тогда правило (3) можно записать так: Λ_i > Λ_jпри всех j ≠ i, (4)

Такое правило максимума правдоподобия реализует критерий идеального наблюдателя при том условии, что все символы передаются равновероятно. Для двоичной системы правило (4) сводится к проверке неравенства Λ₁>Λ₀ (5). В технике связи преимущественно применяют правило максимального правдоподобия (4), (5). В том случае, когда все символы передаются равновероятно, правило максимального правдоподобия реализует критерий идеального наблюдателя.