Модели непрерывных каналов связи.Канал с аддитивным гаусовским шумом.итд

Сигнал на выходе канала с аддитивным гауссовским шумом

Z(t) = у u(t - 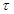) + N(t) = s(t) + N(t), где N(f) — гауссовский аддитивный шум с нулевым математическим ожидани­ем и заданной корреляционной функцией. Чаще всего рассматривается белый гауссовский шум (БГШ) либо квазибелый (с равномерной спектральной плот­ностью в полосе спектра сигнала s(t)). Часто при анализе можно t не учиты­вать, что соответствует изменению начала отсчёта времени на выходе канала. Некоторое усложнение модели (4.48) получается, если коэффициенты передачи g и запаздывания т считать известными функциями времени:

Z(t)= 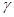(t)u[t- 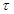(t)]+N(t).Такая модель удовлетворительно описывает многие проводные каналы, ра­диоканалы при связи в пределах прямой видимости, а также радиоканалы с медленными общими замираниями, при которых можно надёжно предсказать значения 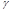и .

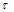модель канала с неопределенной фазой сигнала и аддитивным гауссовским шумом отличается от модели (4.48) тем, что в ней запаздывание является случайной величиной. Для узкополосных сигналов выражение (4.48) при постоянном g и случайных t можно представить в ви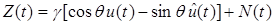де

,где 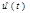— преобразование Гильберта от 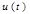; 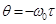^— случайная фаза.