Среднее значение величины

Собственные функции эрмитового оператора 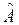образуют ортонормированный базис 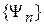. Если частица находится в состоянии Ψ, являющемся суперпозицией функций 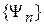, то физическая величина A не имеет определенного значения. Получим ее среднее значение.

Разложение состояния Ψ по базису 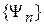имеет вид:

для дискретного спектра

, (2.23)

для непрерывного спектра

, (2.24)

где – комплексное число. Докажем, что коэффициент разложения является амплитудой вероятности обнаружения состояния 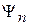в исследуемом состоянии Ψ, а вероятность обнаружения равна .

Коэффициенты разложения . Умножаем на (2.23) или (2.24), интегрируем по пространственным переменным, переставляем суммирование и интегрирование, учитываем условия ортонормированности (2.21) или (2.22). Для дискретного спектра получаем

,

для непрерывного спектра

.

Заменяем 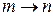, и для дискретного и непрерывного спектров находим коэффициент разложения

. (2.25)

Определим физический смысл коэффициента . Разложение для дискретного спектра подставляем в условие нормировки функции состояния и получаем

.

Результат сравниваем с нормировкой вероятности дискретных событий

,

получаем

. (2.26)

Следовательно, вероятность обнаружения состояния 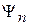в нормированном состоянии 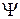равна квадрату модуля коэффициента разложения. С вероятностью обнаруживается в эксперименте значение 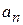дискретной физической величины A для частицы в состоянии 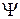, где 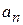– собственное значение оператора 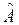с собственной функцией .

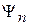Для непрерывного спектра разложение

подставляем в условие нормировки функции состояния

,

учитываем ортонормированность (2.22)

,

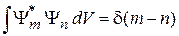получаем

.

Результат сравниваем с нормировкой вероятности непрерывных событий

,

получаем

. (2.27)

Следовательно, плотность вероятности обнаружения состояния 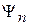в нормированном состоянии 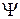равна квадрату модуля коэффициента разложения. С вероятностью в единичном интервале изменения n обнаруживается в эксперименте значение 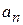непрерывной физической величины A для частицы в состоянии 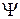, где 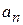– собственное значение оператора 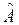с собственной функцией .

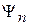Среднее значение величины, описываемой оператором 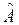, в нормированном состоянии 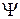равно

, (2.28)

если состояние 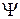нормировано

.

Доказательство для величины A с дискретным спектром:

Состояние 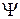разлагаем по собственным функциям 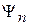оператора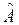

.

Разложение подставляем в (2.28), учитываем

,

,

,

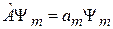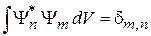получаем

.

Результат совпадает с определением среднего в теории вероятности дискретной величины

.

Следовательно, измерение проектирует состояние частицы Ψ на орты базиса 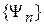, проекцией является амплитуда вероятности . В результате возмущающего воздействия измерительного устройства на микрочастицу происходит необратимое изменение ее состояния, частица оказывается в состоянии 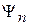с вероятностью . При этом изменяется состояние макроскопического измерительного устройства, оно регистрирует у частицы значение 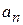физической величины A.

Для непрерывной величины A аналогично находим из (2.28) известное в теории вероятности выражение для среднего

.