Дифракция на круглом отверстии и круглом экране

СОДЕРЖАНИЕ

1. Цель работы……………………………………………………………4

2. Теоретическая часть…………………………………………………..4

2.1. Дифракция света…………………………………………………….4

2.2. Дифракция света на щели…………………………………………..6

2.3. Дифракция на круглом отверстии и круглом экране…………….11

2.4. Дифракционная решетка…………………………………………..12

3. Экспериментальная часть……………………………………………15

3.1. Приборы и принадлежности……………………………………….15

3.2. Описание установки………………………………………………..15

3.3. Требование по технике безопасности…………………………….15

3.4. Выполнение работы………………………………………………..16

4. Контрольные вопросы……………………………………………….19

Список литературы……………………………………………………..19

ЛАБОРАТОРНАЯ РАБОТА № 73

ИЗУЧЕНИЕ ДИФРАКЦИИ СВЕТА НА ПРОСТЕЙШИХ ПРЕГРАДАХ И ДИФРАКЦИОННОЙ РЕШЕТКЕ

Цель работы

1. Ознакомление с дифракцией света на простейших преградах и дифракционной решетке и теорией расчета дифракционной картины в этих случаях.

2. Экспериментальное определение длины волны излучения лазера с помощью дифракционной решетки.

3. Экспериментальное определение с помощью дифракции света ширины щели и размеров мельчайших круглых частиц.

Теоретическая часть

Дифракция света

Под дифракцией света понимают всякое отклонение от прямолинейного распространения света, если оно не может быть объяснено отражением, преломлением или изгибанием световых лучей в средах с непрерывно меняющимся показателем преломления. В частности, дифракция приводит к огибанию световыми волнами препятствий и проникновению света в область геометрической тени.

Явление дифракции света объясняется принципом Гюйгенса-Френеля, согласно которому каждая точка фронта распространяющейся световой волны является источником вторичных сферических когерентных волн. Результирующее колебание в точке наблюдения определяется интерференцией вторичных элементарных волн. Принцип Гюйгенса-Френеля является основным принципом волновой оптики. Выведем на его основе выражение для определения интенсивности в произвольной точке.

Пусть L – источник света (рис. 2.1), произвольная точка А фронта S распространяющей световой волны является источником вторичных сферических волн, Р – точка наблюдения. Амплитуда сферической волны пропорциональна площади элемента dS волнового фронта и убывает с расстоянием r от источника пропорционально 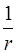каждого элемента dS волновой поверхности. В точку Р (рис. 2.1) приходит колебание

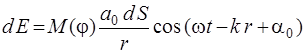, (2.1)

где 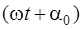– фаза колебаний в месте расположения волновой поверхности S, k – волновое число ( 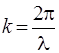, λ – длина волны), r – расстояние от dS до точки Р. Множитель а₀ определяется амплитудой светового колебания в том месте, где находится dS. Коэффициент 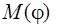зависит от угла 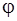между r и нормалью 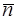к площадке dS (при 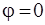он максимален, при 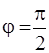он равен нулю).

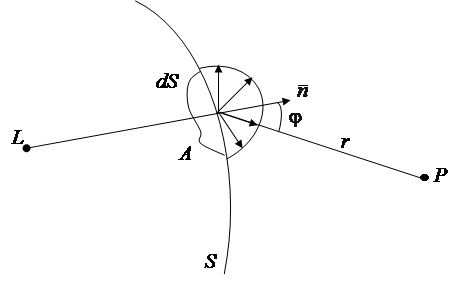Рис. 2.1

Результирующее колебание в точке Р представляет собой суперпозицию колебаний (2.1), взятых для всей волновой поверхности S:

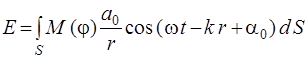. (2.2)

Формула (2.2) является аналитическим выражением Гюйгенса-Френеля. Вычисление непосредственно по этой формуле в общем случае представляет достаточно сложную математическую задачу.

Применение метода зон Френеля, использующего свойства симметрии фронта световой волны, позволяет в ряде случаев упростить вычисление амплитуды результирующего колебания, сводя его к простому алгебраическому суммированию. Этот метод дает возможность определить пространственное расположение максимумов и минимумов дифракционной картины и их величину, однако он не позволяет получить аналитическое выражение, описывающее интенсивность света в любой точке дифракционной картины.

Дифракция света на щели

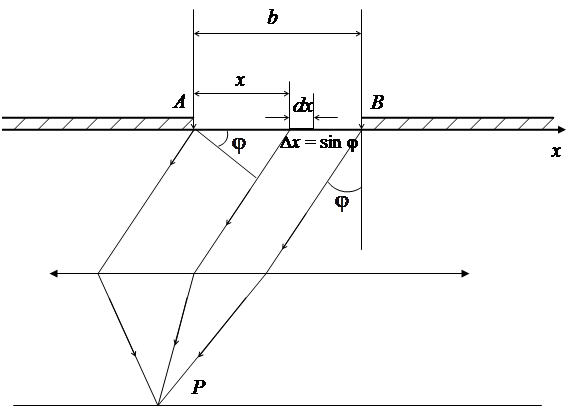Рассмотрим дифракцию в параллельных лучах (дифракцию Фраунгофера) на одной щели. Пусть плоская световая волна падает перпендикулярно на экран с бесконечно длинной узкой щелью шириной b (рис. 2.2) и пусть b >> λ (это условие позволяет не учитывать так называемые краевые эффекты, обусловленные взаимодействием электромагнитного поля падающей световой волны с веществом щели).

Рис. 2.2.

Фронт волны, плоскость щели и экран, на котором ведется наблюдение, параллельны друг другу, а щель бесконечна, поэтому картина, наблюдаемая в любой плоскости, перпендикулярной щели, одинакова и достаточно рассмотреть одну из них (рис. 2.2). Рассмотрим лучи, дифрагированные под углом 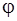к их первоначальному направлению. Каждая точка сечения АВ фронта световой волны является источником вторичных когерентных волн, причем фазы колебаний всех этих источников одинаковы, так как плоскость щели совпадает с плоскостью фронта волны, который для всех них одинаково наклонен к направлению наблюдения. Введем координатную ось х с началом в точке А (рис. 2.2) и направленную от А к В. Выберем элемент фронта световой волны в виде полоски dx, параллельной краям щели. Амплитуда волны dE, обусловленной одним таким элементом, пропорциональна его площади и, следовательно ширине dx, т.е. dE = с dx. Коэффициент пропорциональности с определиться из условия, что по направлению 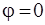амплитуда волны, посылаемой всей щелью, равна Е₀, откуда 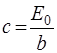и, следовательно

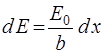. (2.3)

Для нахождения действия всей щели в направлении 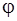необходимо учесть фазы, характеризующие волны, доходящие от различных элементов волнового фронта до точки наблюдения Р (рис. 2.2). Заметим, что линза не вносит дополнительной разности фаз в проходящие через нее лучи. Поэтому разность фаз между рассматриваемыми колебания образуется на пути Δх = sin φ. Если фазу колебания, возбуждаемого элементом, примыкающим к левому краю щели (х = 0) принять равной ωt, то фаза колебания, возбуждаемого элементом, с координатой х будет равна

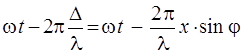, (2.4)

где λ – длина волны света в данной среде. Следовательно, колебание, возбуждаемое элементом с координатой х в точке Р, положение которой на экране определяется углом φ, может быть представлено в виде

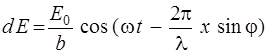. (2.5)

Проинтегрировав это выражение по всей ширине щели, найдем результирующее колебание, возбуждаемое в точке Р открытым участком волновой поверхности:

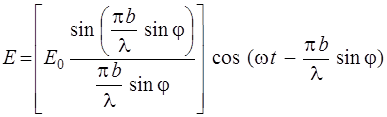. (2.6)

Модуль выражения в квадратных скобках дает амплитуду Е_φ результирующего колебания в точке Р, положение которой определяется углом φ:

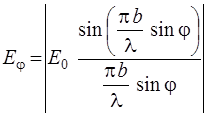. (2.7)

При значениях φ, удовлетворяющих условию 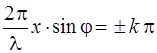, числитель в (2.7) обращается в нуль. Следовательно, положение минимумов определиться из условия

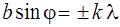. (2.8)

Положение максимумов определить труднее. Находя экстремумы функции Е_φ, легко прийти к трансцендентному уравнению вида

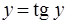, (2.9)

где .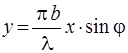

Графическое решение этого уравнения дает корни:

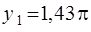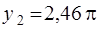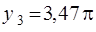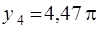, , , и т.д.

Отсюда можно получить значения синусов углов, соответствующих максимумам дифракционной картины.

Заметим, что метод зон Френеля для максимумов дает несколько отличные значения:

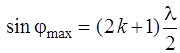, (2.10)

где k = 1, 2, 3, 4, …

Различие обусловлено тем, что метод зон Френеля является приближенным и не учитывает ряд факторов, таких как, например, зависимость амплитуды элементарных волн от угла φ (рис. 2.1) и некоторых других. В табл. 2.1 приведены значения синусов углов φ_max, полученных путем точного решения уравнения (2.9) и даваемых методом зон Френеля.

Таблица 2.1

№ п/п		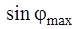Точное решение	Метод зон Френеля
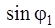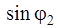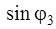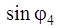		1,43 λ/b 2,46 λ/b 3,47 λ/b 4,47 λ/b	1,5 λ/b 2,5 λ/b 3,5 λ/b 4,5 λ/b

Интенсивность света I пропорциональна квадрату амплитуды, поэтому из (2.7) получаем

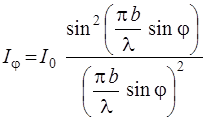, (2.11)

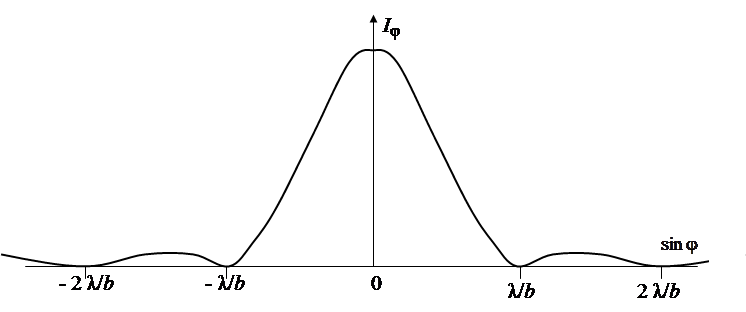где I₀ – интенсивность в центре дифракционной картины (φ = 0). Вид этой функции показан на рис. 2.3.

Рис. 2.3

Величина вторичных максимумов быстро убывает (рис. 2.3). Подставив значения 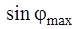в (2.11), можно получить отношения интенсивностей максимумов:

1 : 0,0472 : 0,0165 : 0,0083 : 0,0050. (2.12)

При изучении дифракции света удобнее бывает измерять не углы дифракции, а расстояния между максимумами или минимумами на экране и расстояние от экрана до щели.

Из рис. 2.4 видно, что

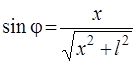, (2.13)

где х – расстояние от центра экрана до точки наблюдения, l – расстояние от экрана до щели. В соответствии с (2.8) и табл. 2.1 положение минимумов будет определяться из условия

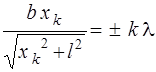. (2.14)

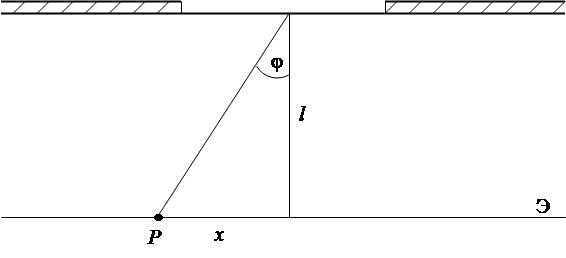Рис. 2.4

Положение максимумов

;

;

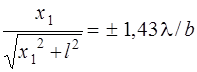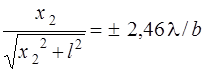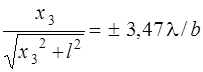; (2.15)

.

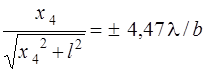Дифракция на круглом отверстии и круглом экране

Дифракция света на бесконечно длинной узкой щели, рассмотренная в предыдущем разделе, является по сути, одномерной задачей, решение которой зависит одной переменной – угла дифракции φ. Дифракция на круглом отверстии или экране – двумерная задача, ее решение зависит как угла φ (рис. 2.2), так и некоторого угла Θ, определяющего положение в направлении, перпендикулярном плоскости чертежа (рис. 2.2). Получение решения в общем виде представляет достаточно сложную математическую задачу и в данном пособии не рассматривается, будут приведены только окончательные результаты. Заметим, что метод зон Френеля, используемый обычно при рассмотрении дифракции света на круглом отверстии или на экране, позволяет определить интенсивность света в центре дифракционной картины, но не описывает распределения интенсивности по всей поверхности экрана, на котором ведется наблюдение. Задача расчета амплитуды приводится к функциям Бесселя, общий вид которых подобен рис. 2.3, но несколько круче спадающий по мере роста φ. Дифракционная картины представляет из себя ряд темных и светлых колец, в центре которых в зависимости от размеров отверстия может быть максимумом (укладывается нечетное число зон Френеля) или минимумов (укладывается четное число зон Френеля). Угловой радиус темных колец определяется приближенно соотношением

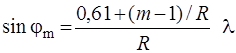, (2.16)

где R – радиус отверстия и m = 1, 2, … В табл. 2.2. приведены значения радиусов темных и светлых колец и относительная интенсивность в максимумах (рассмотрен случай, когда в центре – максимум).

Таблица 2.2

Минимумы	Максимумы	Интенсивность
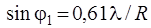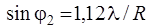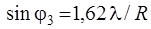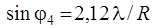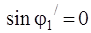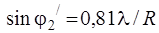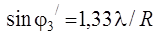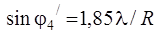		0,0175 0,0042 0,0016

Распределение интенсивности в случае дифракции на круглом непрозрачном экране аналогично случаю дифракции на круглом отверстии, но в этом случае в центре дифракционной картины всегда будет максимум.

Дифракционная решетка

Простейшая одномерная дифракционная решетка представляет собой систему из большого числа N одинаковых по ширине и параллельных друг другу щелей, лежащих в одной плоскости и разделенных непрозрачными промежутками одинаковой ширины. Рассмотрим пропускающую дифракционную решетку (рис. 2.5).

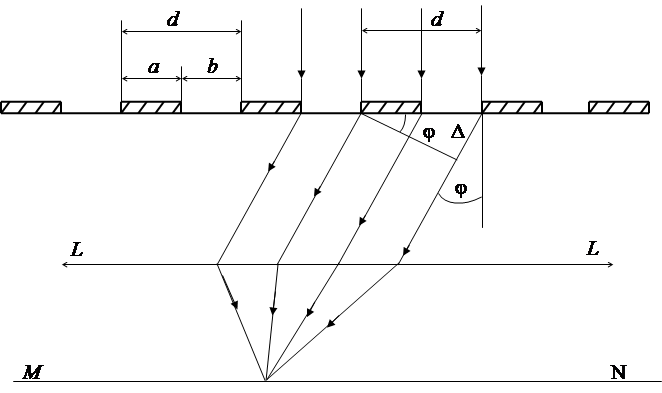
Рис. 2.5

Величина d = a + b называется периодом, или постоянной дифракционной решетки (a – ширина непрозрачных, а b – прозрачных промежутков). Плоская монохроматическая волна с длиной λ падает нормально на дифракционную решетку, в фокальной плоскости собирающей линзы LL помещен экран МN, на котором ведется наблюдение.

Если волна падает нормально к плоскости решетки, то ее фронт совпадает с плоскостью решетки. Поэтому все щели решетки излучают вторичные волны в одной фазе. Кроме дифракции от отдельных щелей, происходит сложение колебаний от каждой из них, т.е. происходит интерференция многих пучков. Если число щелей N , то интерферируют между собой N пучков.

Из рис. 2.5 видно, что оптическая разность хода Δ от двух соседних щелей есть

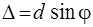, (2.17)

чему соответствует разность фаз

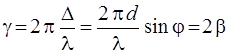, (2.18)

где .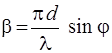

Амплитуда колебаний, даваемых одной щелью, определяется выражением (2.7) вида

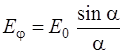, (2.19)

где .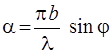

Суммируя действие отдельных щелей и учитывая разность фаз (2.18), можно получить результирующую амплитуду:

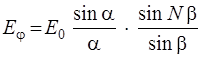, (2.20)

где N – число щелей, Е₀ – амплитуда. Задаваемая одной щелью в направлении φ = 0.

Множитель 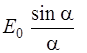выражает действие одной щели, а множитель 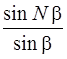– интерференцию волн от всех N щелей. Распределение интенсивности в дифракционной картине будет иметь вид

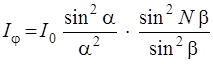. (2.21)

Находя экстремумы функции (2.20), можно определить положение главных максимумов, однако это достаточно длинный путь, поэтому воспользуемся результатом, даваемым графическим методом (в данной работе не рассматривается). Условие главных максимумов имеет вид

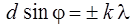. (2.22)

Распределение интенсивности (2.21) в дифракционной картине, даваемой решеткой, показано на рис. 2.6.

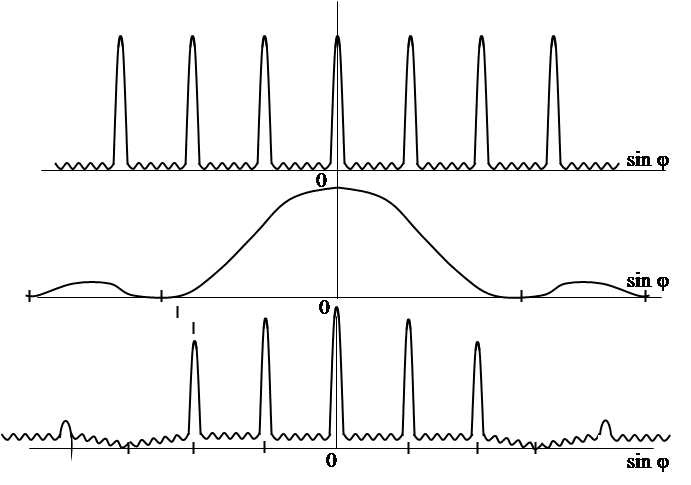На рис. 2.6, а показан график функции 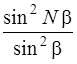, описывающей интерференцию света от N щелей, на рис. 2.6, б – график функции 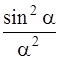, описывающей распределение интенсивности при дифракции от одной щели, на рис. 2.6, в – произведение графиков (а) и (б), описывающее реальное распределение интенсивности при дифракции на решетке.

Помимо главных максимумов, в дифракционной картине есть вторичные максимумы, интенсивность которых значительно меньше, в результате чего они практически не наблюдаются. Между двумя главными максимумами располагается (N–1) добавочных максимумов, определяемых условием

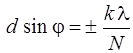. (2.23)

Экспериментальная часть

Приборы и принадлежности

- оптический квантовый генератор с блоком питания,

- оптическая скамья с экраном для наблюдения,

- дифракционная решетка в держателе,

- образец с ликоподием и мелкой сеткой в держателях и раздвижной щелью.

Описание установки

Основой установки является оптическая скамья со шкалой, на одном конце которой установлен в специальном держателе оптический квантовый генератор (лазер), служащий источником монохроматического излучения. На противоположном конце скамьи изготовлен экран с делениями, на котором наблюдается дифракционная картина. Между экраном и оптическим квантовым генератором на скамью устанавливаются в держателях образцы или дифракционная решетка.