Воспроизведение непрерывного сигнала

Известно, что функция вида 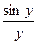представляет собой реакцию идеального фильтра нижних частот с граничной частотой 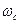на дельта-функцию. Следовательно, если в приемном устройстве поместить такой фильтр и пропустить через него квантованный сигнал, представляющий собой последовательность с частотой 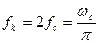весьма кратковременных импульсов, амплитуды которых пропорциональны отсчетам исходной непрерывной функции, то, суммируя выходные сигналы фильтра, можно воспроизвести с достаточно высокой степенью точности исходный непрерывный сигнал.

Однако нас интересует случай, когда сигнал x(t) ограничен во времени (T_c). В этом случае сумма (1.70) будет конечной

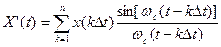, (1.71)

где .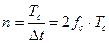

Усечение бесконечной суммы, т.е. ограничение ее теми значениями X_k, которые оказываются в пределах T_c, уменьшает точность представления сигнала x(t).

Это первый фактор, определяющий точность представления.

Кроме того, сигнал конечной длительности имеет бесконечный спектр гармонических составляющих. Поэтому ограничение спектра сигнала некоторой частотой 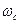является вторым фактором, снижающим точность представления непрерывного сигнала x(t) дискретными отсчетами.

Средний квадрат относительной погрешности в этом случае определяется выражением

,

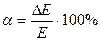где Е – полная энергия неограниченного спектра сигнала;

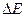- энергия «хвоста» спектра, т.е. той его части, которая расположена за пределами f_c .

Чтобы погрешность формулы (1.71) была мала, должно выполняться условие

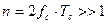. (1.72)

Дополнительная погрешность вносится при восстановлении сигнала x(t) за счет неидеальности фильтра нижних частот, т.к. идеальный фильтр НЧ физически нереализуем (предполагает наличие отклика на 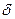-функцию при t<0, т.е. до начала подачи на вход).

Однако на практике никогда не требуется идеально точное воспроизведение передаваемого сигнала, поэтому ограничивают спектр сигнала диапазоном с верхней частотой 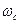, в котором сосредоточена основная энергия сигнала.

Дисперсия приведенной погрешности, возникающей в результате усечения, будет

,

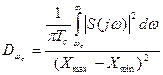где 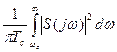- средняя мощность отсекаемой части спектра;

T_c – длительность сигнала;

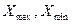- идеальные значения x(t).

Возможно и следующее представление

,

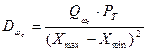где 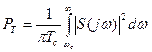- средняя мощность сигнала

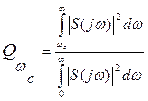- относительная площадь отсекаемого участка энергетического спектра x(t).

По заданной величине 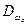и известных 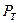, , 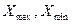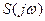можно определить .

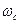а) Используются и следующие критерии оценивания:

.

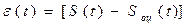б) Максимальная абсолютная и относительная ошибки:

,

.

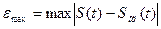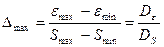в) Эффективная относительная ошибка

.

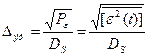г) Средняя относительная ошибка

.

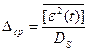д) Среднеквадратическая ошибка

.
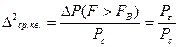