Проверка адекватности полученной модели

Содержание

1. Задание............................................................. ……………………….3

2. Построение математической модели объекта по экспериментальной переходной характеристике………………………………….…………………..4

2.1 Расчет коэффициентов передаточной функции модели………….…..6

2.2 Проверка адекватности полученной модели……………………….….7

3. Расчет оптимальных настроечных параметров цифровых регуляторов………………………………………………………………………..9

3.1 Модель и расчетная схема цифровой АСР………………….………....9

3.2 Алгоритмы вычислительных устройств цифровых регуляторов…...11

3.3 Запас устойчивости систем с цифровыми регуляторами……………12

3.4 Последовательность расчета оптимальных настроечных
параметров…………………………………………………………………….…14

3.5 Результаты расчета………………………………………………….….15

4. Расчёт переходных процессов в цифровых АСР……………………..17

5. Выводы………………………………………….……………………….22

Список литературы…………………………….………………………….23

Задание

Провести расчет и исследование динамики автоматической системы регулирования. В системе осуществляется регулирование давления.

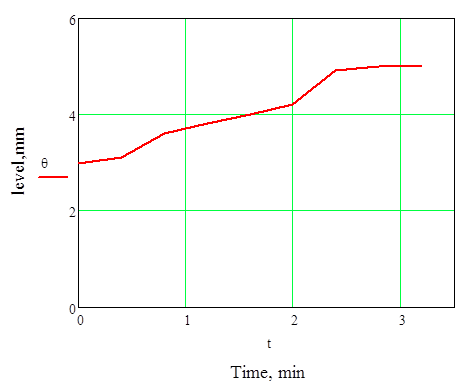
Канал регулирующего воздействия (изменение задания регулятору на 0,5 кгс/см²) - кривая разгона объекта:

t, мин		0,4	0,8	1,2	1,6		2,4	2,8	3,2
Р, кгс\см2		3,1	3,6	3,8		4,2	4,9

Канал возмущающего воздействия (изменение давления на 20% хода регулирующего органа) - передаточная функция объекта в виде апериодического звена 1-го порядка:

;

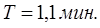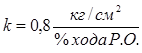
Заданная кривая разгона:

t, мин

2 Построение математической модели объекта по экспериментальной переходной характеристике.

Построение математической модели линейной системы по экспериментальной переходной характеристике (кривая разгона) производится в следующем порядке:

1.На основании формы кривой разгона и в зависимости от физических свойств исследуемой системы устанавливается вид передаточной функции модели.

2.Определяются значения коэффициентов передаточной функции из условия наилучшего приближения модели к объекту.

3.Производится оценка точности аппроксимации.

Произведем расчет коэффициентов передаточной функции модели методом площадей Симою М.П.

Для расчета параметров модели методом площадей целесообразно ввести нормированную кривую разгона, определяемую формулой:

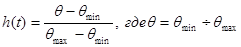
Предполагается, что порядок передаточной функции модели выбирается априорно, и задача расчета сводится к определению параметров модели. Зададимся следующими структурами передаточной функции модели:

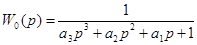
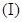
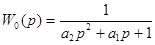
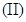
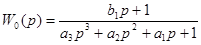
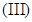
Выражение l/W₀(p) - обратное передаточной функции модели, можно разложить в ряд по степени р:

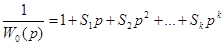
Очевидно, что для модели (I):

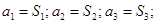
для модели (II):

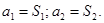
Для модели (III) коэффициенты b₁, a₁, a₂, а₃ связаны с коэффициентами S₁, S₂, S₃, S₄ системой уравнений:

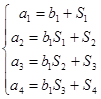
Коэффициенты S, связаны с переходной функцией h(t) соотношениями:

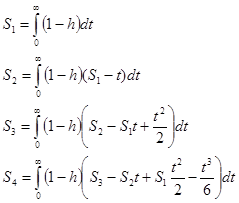
2.1 Расчет коэффициентов передаточной функции модели:

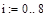Таким образом, математическая модель переходной функции по каналу регулирования имеет вид:

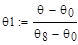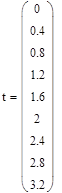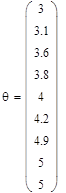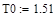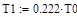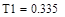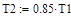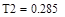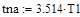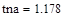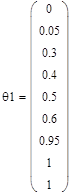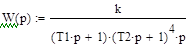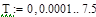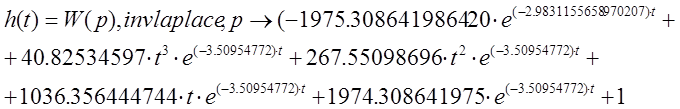
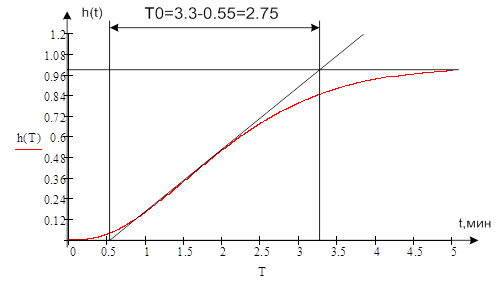
Проверка адекватности полученной модели.

Заключительным этапом построения математической модели объекта является оценка точности аппроксимации. Обычно принимают, что модель адекватна объекту, если разность между ординатами нормированных переходных функций модели и объекта не превышает 0,15.

Расчет переходной функции модели произведем с помощью обратного преобразования Лапласа.

Совмещенное изображение нормализованной кривой разгона и переходной функции модели:

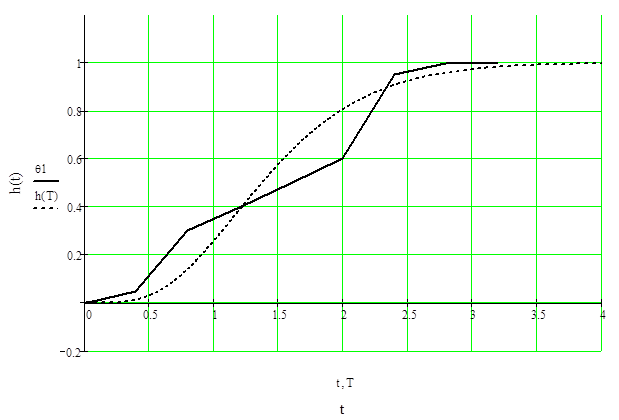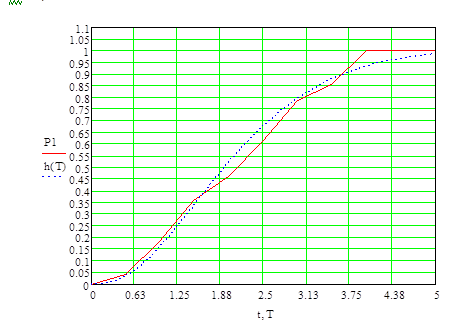
Расхождение не превышает 0.15, что является допустимым.