Дисперсия света. Электронная теория дисперсии. Ход белого луча в призме. Вывод формулы для угла отклонения лучей призмой.
Дисперсия – явление зависимости показателя преломления от длинны волны. Впервые это явление наблюдал Ньютон. Потом была выведена полуимперическая формула (формула Каши): 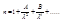 (для воздуха)
(для воздуха) 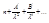 , где
, где 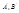 -- выбирались экспериментально. Позже, когда был открыт электрон(1895г.) была открыта электронная теория дисперсии: под действием электромагнитной волны электрон совершает колебания.В результате электрон отклоняется от положения равновесия и образует дипольный момент:
-- выбирались экспериментально. Позже, когда был открыт электрон(1895г.) была открыта электронная теория дисперсии: под действием электромагнитной волны электрон совершает колебания.В результате электрон отклоняется от положения равновесия и образует дипольный момент: 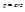 , r – отклонение от положения равновесия, N- число электронов (p=erzN) с другой стороны
, r – отклонение от положения равновесия, N- число электронов (p=erzN) с другой стороны 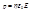 , где
, где 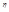 - диэлектрическая проницаемость поля, E – напряжённость поля
- диэлектрическая проницаемость поля, E – напряжённость поля 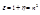
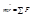 С одной стороны F – сила, возвращающая сила
С одной стороны F – сила, возвращающая сила 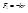 . При своём движении она испытывает некоторое сопротивление:
. При своём движении она испытывает некоторое сопротивление: 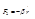 , где
, где 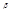 - постоянная сопротивления среды.Третья сила :
- постоянная сопротивления среды.Третья сила : 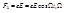 - частота колебаний электрона. Таким образом
- частота колебаний электрона. Таким образом 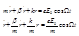
Решение имеет следующий вид: 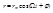 под cos стоит частота вынуждающей силы.
под cos стоит частота вынуждающей силы. 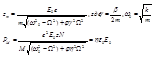
N - концентрация
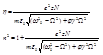


 Показатель преломления зависит от частоты вынужденных и собственных колебаний.
Показатель преломления зависит от частоты вынужденных и собственных колебаний. 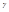 - очень мал.
- очень мал. 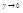
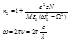
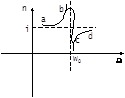 |
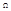 - вынужденные колебания.На практике разрыва второго рода не может быть. Когда
- вынужденные колебания.На практике разрыва второго рода не может быть. Когда 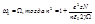 Пренебречь
Пренебречь 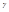 -нельзя
-нельзя 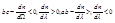 Этот участок называется участком аномальной дисперсии. Он наблюдается внутри линии поглощения. Участок ab
Этот участок называется участком аномальной дисперсии. Он наблюдается внутри линии поглощения. Участок ab
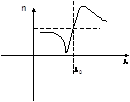 |
называется участком нормальной дисперсии. 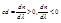 - тоже участок нормальной дисперсии. На участке нормальной дисперсии показатель преломления с увеличением длинны волны падает.
- тоже участок нормальной дисперсии. На участке нормальной дисперсии показатель преломления с увеличением длинны волны падает.
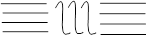 Явление аномальной дисперсии широко применяется лазерной интерферометрии
Явление аномальной дисперсии широко применяется лазерной интерферометрии 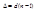
Меряется концентрация неизвестных атомов. Метод аномальной дисперсии получил название метода кругов Рождественского.Крюки – искривление. Меряется концентрация по расстоянию между крюками.Исследуем формулу для разных частотных интервалов для нормальной дисперсии. 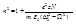
1). 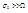 - радиомагнитные волны и низко частотный диапазон (переменные волны)
- радиомагнитные волны и низко частотный диапазон (переменные волны) 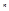 - const Это волны дисперсии не испытывают, поэтому возможна радиосвязь.
- const Это волны дисперсии не испытывают, поэтому возможна радиосвязь.
2). 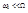 (рентгеновские лучи и
(рентгеновские лучи и 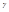 - лучи)
- лучи)
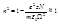 Рентгеновские и
Рентгеновские и 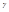 - лучи вообще не испытывают преломления. Вывод:явление дисперсии наблюдается только для диапазона, т.е. когда
- лучи вообще не испытывают преломления. Вывод:явление дисперсии наблюдается только для диапазона, т.е. когда 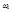 и
и 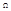 сравнимы друг с другом.
сравнимы друг с другом.
Вывод формулы для угла отклонения лучей призмой.
Пусть луч AB падает на одну из граней призмы. Преломившись в точке B, луч пойдёт по направлению BC и, вторично преломившись в точке С, выйдет из призмы в воздух. Найдём угол 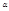 , на который луч, пройдя через призму, отклонится от первоначального направления. Этот угол мы будем называть углом отклонения.Угол между преломляющими гранями, называемый преломляющим углом призмы,обозначим
, на который луч, пройдя через призму, отклонится от первоначального направления. Этот угол мы будем называть углом отклонения.Угол между преломляющими гранями, называемый преломляющим углом призмы,обозначим  . Из четырехугольника BOCN, в котором углы при В и С прямые,найдём, что угол BNC равен
. Из четырехугольника BOCN, в котором углы при В и С прямые,найдём, что угол BNC равен 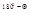 .Пользуясь этим, из четырёхугольника BMCN находим
.Пользуясь этим, из четырёхугольника BMCN находим 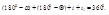 (1).Отсюда
(1).Отсюда 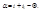 (2).(рис9)
(2).(рис9)
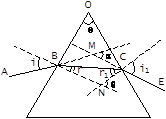 |
Угол  , как внешний угол в треугольнике BCN, равен
, как внешний угол в треугольнике BCN, равен 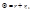 (3).где r – угол преломления в точке В, а
(3).где r – угол преломления в точке В, а 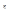 - угол падения в точке С луча, выходящего из призмы.Далее, пользуясь законом преломления имеем
- угол падения в точке С луча, выходящего из призмы.Далее, пользуясь законом преломления имеем 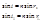 (4).
(4).
С помощью полученных уравнений, зная преломляющий угол призмы 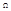 и показатель преломления n, мы можем при любом угле падения i вычислить угол отклонения
и показатель преломления n, мы можем при любом угле падения i вычислить угол отклонения 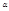 .Особенно простую форму получает выражение для угла отклонения в том случае, когда преломляющий угол призмы
.Особенно простую форму получает выражение для угла отклонения в том случае, когда преломляющий угол призмы  мал, т.е. призма тонкая, а угол падения i невелик; тогда угол
мал, т.е. призма тонкая, а угол падения i невелик; тогда угол 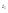 тоже мал. Заменяя приближённо в формулах синуы углов самими углами, имеем i=nr,
тоже мал. Заменяя приближённо в формулах синуы углов самими углами, имеем i=nr, 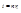 . Подставляя эти выражения в формулу (2) и пользуясь (3), находим
. Подставляя эти выражения в формулу (2) и пользуясь (3), находим 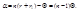 (5).
(5).
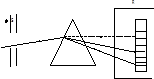
Ход белого луча в призме.(рис10)
27. Излучение Вавилова – Черенкова.
 |
Советский физик п. а. Черенков (1904 – 1990), работавший под руководством Вавилова, показал, что при движении релятивистских заряженных частиц в среде с постоянной скоростью v, превышающей фазовую скорость света в этой среде, т. е. при условии v>c/n (n – показатель преломления среды), возникает электромагнитное излучение, названное впоследствии излучением (эффектом) Вавилова – Черенкова. Природа данного излучения, обнаруженного для разнообразных веществ, в том числе и для чистых жидкостей, подробно изучалась С. И. Вавиловым. Он показал, что данное свечение не является люминесценцией, как считалось ранее, и высказал предположение, что оно связано с движением свободных электронов через вещество.
Излучение Вавилова – Черенкова в 1937 г. было теоретически объяснено советскими учеными И. Е. Таммом(1895-1971) и И.М. Франком(р. 1908) (Черенков, Тамм и Франк в 1958 г. удостоены Нобелевской премии).
Согласно электромагнитной теории, заряженная частица( например, электрон) излучает электромагнитные волны лишь при движении с ускорением. Тамм и Франк показали, что это утверждение справедливо только до тех пор, пока скорость заряженной частицы не превышает фазовой скорости c/n электромагнитных волн в среде, в которой частица движется. Если частица обладает скоростью v>c/n, то, даже двигаясь равномерно, она будет излучать электромагнитные волны. Таким образом, согласно теории Тамма и Франка, электрон, движущийся в прозрачной среде со скоростью, превышающей фазовую скорость света в данной среде, должен сам излучать свет.
Отличительной особенностью излучения Вавилова – Черенкова является его распространение не по всем направлениям, а лишь по направлению, составляющим острый угол J с траекторией частицы, т. е. вдоль образующих конуса, ось которого совпадает с направлением скорости частицы. Определим угол J
cosJ=(c/n)/v=c/(nv).
Возникновение излучения Вавилова – Черенкова и его направленность истолкованы Франком и Таммом на основе представлений об интерференции света с использованием принципа Гюйгенса.
На основе излучения Вавилова – Черенкова разработаны широко используемые экспериментальные методы для регистрации частиц высоких энергий и определения их свойств (направление движения, величина и знак заряда, энергия). Счетчики для регистрации заряженных частиц, в которых используется излучение Вавилова – Черенкова, получили название черенковских счетчиков. В этих счетчиках частица регистрируется практически мгновенно (при движении заряженной частицы в среде со скоростью, превышающей фазовую скорость света в данной среде, возникает световая вспышка, преобразуемая с помощью фотоэлектронного умножителя в импульс тока). Это позволило в1955 г. итальянскому физику Э. Сегре (р. 1905) открыть в черенковском счетчике короткоживущую античастицу – антипротон.
Эффект Доплера в оптике.
Согласно принципу относительности Эйнштейна, уравнение световой волны во всех инерциальных системах отсчёта одинаково по форме. Используя преобразования Лоренца, можно получить уравнение волны, посылаемой источником, в направлении приёмника, в другой инерциальной системе отсчёта, а следовательно и связать частоты световых волн, излучаемых источником (n0) и воспринимаемых источником (n). Теория относительности приводит уравнение описывающее эффект Доплера для электромагнитных волн в вакууме:
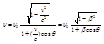 , где v- скорость источника света относительно приёмника, с- скорость света в вакууме.
, где v- скорость источника света относительно приёмника, с- скорость света в вакууме. 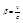 , θ- угол между вектором скорости v и направлением наблюдения, измеряемый в системе отсчёта связанной с наблюдением.
, θ- угол между вектором скорости v и направлением наблюдения, измеряемый в системе отсчёта связанной с наблюдением.
При θ=0, 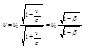 продольный эффект Доплера, наблюдаемый при движении приёмника вдоль линии, соединяющей его с источником. При малых около светных скоростях v(v<<c), разлагая в ряд и пренебрегая числом порядка β2, получим:
продольный эффект Доплера, наблюдаемый при движении приёмника вдоль линии, соединяющей его с источником. При малых около светных скоростях v(v<<c), разлагая в ряд и пренебрегая числом порядка β2, получим:
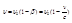
Изменение частоты зависит от 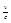 , но для заметного. По величине смещения необходимо перемещать источник света относительно приёмника с большой скоростью.
, но для заметного. По величине смещения необходимо перемещать источник света относительно приёмника с большой скоростью.
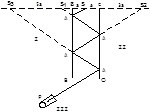 |
В призменный спектрограф, с помощью которого определяется частота света, направлялись лучи, многократно отражённые от двух параллельных зеркал, перемещающихся по отношению к неподвижному источнику света.
S- источник света, находящийся посередине между зеркалами BB1 и CC1,
P- коллиматор призменного спектрографа, в который попадают лучи после n- кратного отражения.
Определим скорость, с которой перемещается мнимый источник света n кратно отраженных лучей в результате перемещения зеркал со скоростью v. Для этого определим местоположение мнимого источника света n-кратных отраженных лучей.
Луч SA отражается от зеркала BB1 так, как если бы он выходил из мнимого источника света S1 отражается от зеркала на таком же расстоянии a как и действительный источник.
Луч, испытывающий n отражений в этих параллельных зеркалах и попадающий в коллиматор призменного спектрографа P, распространяется так, как будто он вышел из мнимого источника, отстающего от зеркала на расстоянии: 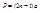 . При изменении расстояния a на (a+Δa), мнимый источник переместится и будет отстоять на расстоянии b+Δb=(2n-1)(d+Δd) но так как само зеркало переместилось на расстояние Δa то по отношению к неподвижным телам источник переместится на расстояние Δb’=Δb-Δa=2(n-1)Δa
. При изменении расстояния a на (a+Δa), мнимый источник переместится и будет отстоять на расстоянии b+Δb=(2n-1)(d+Δd) но так как само зеркало переместилось на расстояние Δa то по отношению к неподвижным телам источник переместится на расстояние Δb’=Δb-Δa=2(n-1)Δa
Поэтому если привести зеркала BB1 и CC1 по отношению к источнику света в движение со скоростью 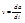 , но мнимый источник света сответственный n простым отражённым лучам, будет перемещаться по отношению к спектрографу, с помощью которого измеряется длина волны световых лучей со скоростью
, но мнимый источник света сответственный n простым отражённым лучам, будет перемещаться по отношению к спектрографу, с помощью которого измеряется длина волны световых лучей со скоростью 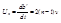 ,которая в 2(n-1 ) раз превышает скорость действительного перемещения зеркал.
,которая в 2(n-1 ) раз превышает скорость действительного перемещения зеркал.
Тепловое излучение.
Тепловым излучением называется излучение нагретых тел. Все тела обладают тепловым излучением. Основная особенность теплового излучения – равновесность (тепловое излучение – это единственное равновесное излучение). Это означает, что количество излученной энергии и количество поглощенной в замкнутой системе равны.все остальные виды излучений наз. люминисценциями.
Тепловое излучение – это электромагнитное излучение, возникающее за счет внутренней энергии излучающего тела и зависящее только от температуры и оптических свойств этого тела
Основные характеристики.
Энергетическая светимость
Спектральная плотность энергетической светимости.
Энергетическая светимость – это количество энергии испускаемой с единицы площади за единицу времени. R(T)=d2W/(dSdT);(Вт/м2)
Спектральная плотность энергетической светимости – это количество тепловой энер 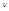 гии испускаемой с единичной поверхности в единицу времени в интервале частот от
гии испускаемой с единичной поверхности в единицу времени в интервале частот от 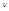 до
до 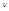 +d
+d 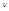 .
.
r(λ,T)=d2W/(dSdtdλ)=dR/dλ (Вт/м2м)
R= 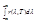
Закон Кирхгофа: отношение спектральной плотности энергетической светимости к поглащательной способности при данной длине волны и температуре есть универсальная функция.
r(λ,T)arT= r(λ,T)/ a(λ,T)
Закон Стефана – Больцмана: энергетическая светимость черного тела пропорциональна четвертой степени его термодинаической температуры
R0э=σT4
Закон Вина: частота, соответствующая максимальному значению энергетической светимости черного тела, прямо пропорциональна его термодинамической температуре.
b1= 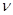 m /T, где b1 - постоянная величина.
m /T, где b1 - постоянная величина.
Абсолютно черное тело – это тело , если оно при любой температуре полностью поглощает всю энергию падающих на него электромагнитных волн независимо от их частоты, поляризации и направления распространения.
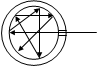 |
Модель а.ч.т. – это полость с отверстием больших размеров произвольной формы с теплоизолированными стенками и зеркальной внутренней поверхностью. Отверстие является а.ч.т. Свет попадает в отверстие , многократно отражаясь внутри полости. Вероятность выхода луча  0.Отверстие излучает энергию в виде тепла.
0.Отверстие излучает энергию в виде тепла.
30. Излучение черного тела. Формулы Релея-Джинса, Вина, Планка для теплов. излучения черного тела. Вывод формулы Планка.
Тело называется абсолютно черным (абс.ч.т.), если его поглощательная способность 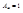 для излучения всех частот. Тогда,
для излучения всех частот. Тогда, 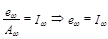 . Поэтому равновесное излучение наз. также черным излучением. Т.к.
. Поэтому равновесное излучение наз. также черным излучением. Т.к. 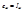 , а равновесное излучение изотропно, то излучательная способность абс.ч.т. одинаково по всем направлениям. Распределение энергии в спектре абс.ч.т.(рис.1).
, а равновесное излучение изотропно, то излучательная способность абс.ч.т. одинаково по всем направлениям. Распределение энергии в спектре абс.ч.т.(рис.1).
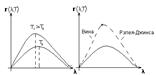 |
Ф-ла Релея-Джинса: 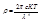 .
.
Ф-лы Вина: 1) 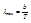 , где
, где 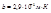 . 2)
. 2) 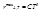 , где
, где 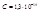
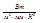 .
.
Ф-ла Планка: 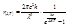 .
.
Вывод ф-лы Планка. Он исходил из того, что т.к. тепловое излучение равновесно, то в любой момент времени, достаточно большой по сравнению с атомными временами ( 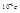 ) число атомов испускания должно быть = числу атомов поглощения. Первоначально теорию излучения создал Эйнштейн. Она заключается в след.: атом излуч. и поглощает только, если переходит с одного энергетического уровня на другой.(рис.)
) число атомов испускания должно быть = числу атомов поглощения. Первоначально теорию излучения создал Эйнштейн. Она заключается в след.: атом излуч. и поглощает только, если переходит с одного энергетического уровня на другой.(рис.)
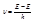
 |
1 переход - вынужденное поглощение. Вероятность этого перехода 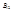 - коэффиц. поглощения Эйнштейна. Интенсивность поглощения:
- коэффиц. поглощения Эйнштейна. Интенсивность поглощения: 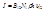 , где
, где 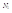 -заселенность энерг.ур 1,
-заселенность энерг.ур 1, 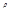 -плотность светового потока. Переход со 2 на 1ур.-спонтанное излучение. Вероятность:
-плотность светового потока. Переход со 2 на 1ур.-спонтанное излучение. Вероятность: 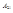 . Интенсивность излучения:
. Интенсивность излучения: 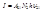 .
.
2 переход - вынужденное издучение. Вероятность: 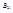 . Интенсивность:
. Интенсивность: 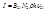 . Вынужденный фотон абсолютно когерентен.
. Вынужденный фотон абсолютно когерентен.
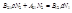 - условие равновесия.
- условие равновесия.
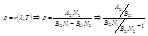
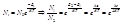 .
.
1) Пусть 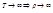
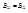 .
.
2) 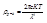
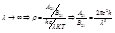 Следовательно,
Следовательно, 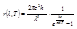 . - ф-ла Планка.
. - ф-ла Планка.
Вывод законов теплового излучения (законов Вина, Стефана-Больцмана) из формулы Планка.
Закон Вина и закон Стефана-Больцмана являются следствием формулы Планка. Согласно формуле Планка, интегральная плотность энергии равновесного излучения в вакууме равна:
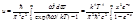
 ,
, 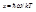 .
.
Разложив знаменатель 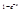 в ряд и интегрируя, получим для последнего интеграла:
в ряд и интегрируя, получим для последнего интеграла:
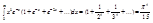 , отсюда:
, отсюда: 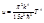 .
.
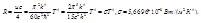
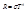 - закон Стефана-Больцмана.
- закон Стефана-Больцмана.
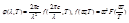 , F – некоторая функция отношения частоты к температуре.
, F – некоторая функция отношения частоты к температуре.
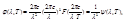 |
где
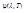 - некоторая функция произведения
- некоторая функция произведения 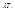
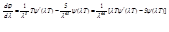
Выражение в квадратных скобках представляет некоторую функцию 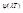 .
.
При длине волны 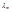 , соответствующей максимуму функции
, соответствующей максимуму функции 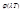 , выражение должно обращаться в нуль:
, выражение должно обращаться в нуль: 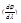
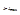
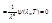
 , поэтому
, поэтому 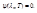
Продифференцируем формулу Планка:
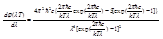 .
.
Обозначив 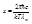 получим:
получим: 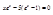
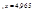
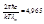 , откуда
, откуда 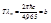 - закон Вина.
- закон Вина.
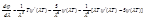 |
