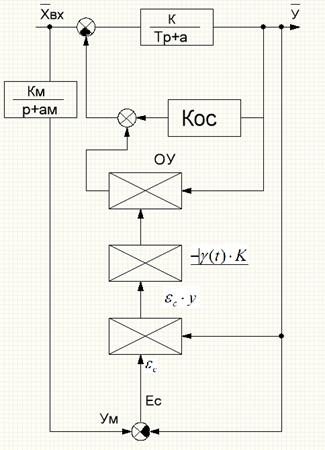
Квазиоптимальное управление

Автоматическое управление при законах близких к оптимальным называется квазиоптимальным управлением, ну а сами системы квазиоптимальными.

Основные причины не позволяющие точно реализовать оптимальное управление:

1).Не идеальность математической модели объекта, любая модель приближённо описывает реальный объект;

2).Упрощение принимаемых законов управления при оптимизации конкретной системы;

3).Не идеальность характеристик реальных элементов используемых при идеализации систем.

На практике пользуются принципом А.Д. Шуфлинского. Он заключается в том, что любой объект можно описать ДУ второго или 3-го порядка, т.е. малые инерционности можно не учитывать.

В ряде случаев для управления вместо знакопеременного сигнала используют знакопостоянный (это не требует реверсивного преобразования).

Рассмотрим пример:

;

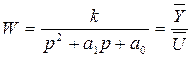Корни комплексно-сопряжённые: ;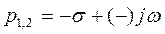

; ; .

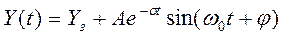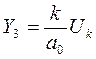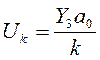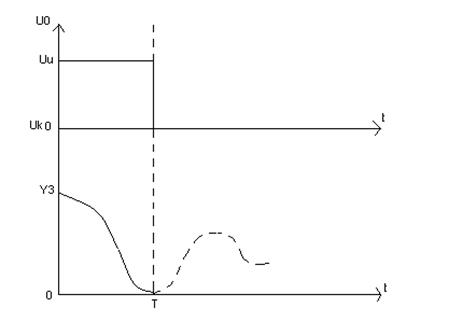
Т.к. корни комплексно-сопряжённые, то теорема об двух интервалах не действительна. При комплексно-сопряжённых корнях может быть множество интервалов управления.

; ;

; ;

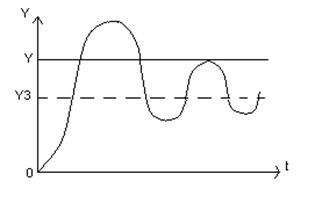
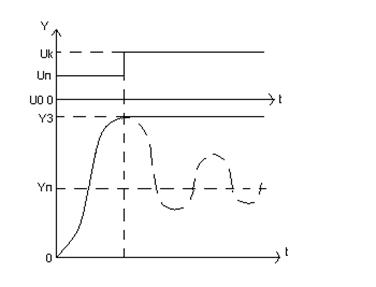
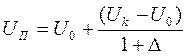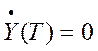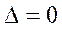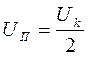35.Самонастраивающаяся система управления. Принципы построения самонастраивающихся САУ. Адаптивное управление

При недостаточности априорной информации об объекте с переменными параметрами необходимо решать 2 задачи: решать и изучать объект в процессе его функционирования и управлять им. Задачу изучении объекта можно совместить с задачей управления. При управлении можно получать доп инфу об объекте, т.е. управление носит двойственный характер. Широко распространенной на практике задачей является стабилизация динамических свойств промышленных объектов, для которых переходные режимы играют существенную роль. Например в электроприводах роботов и манипуляторов могут изменяться в широких диапазонах, поэтому жёсткость не обеспечивает заданное значение динамических свойств. Примером может служить резанье на металлорежущем станке.

Системы:

1) настраиваемые (программные)

2) Самонастраивающиеся (адаптивные)

Блок-схема самонастраивающейся системы будет иметь вид:

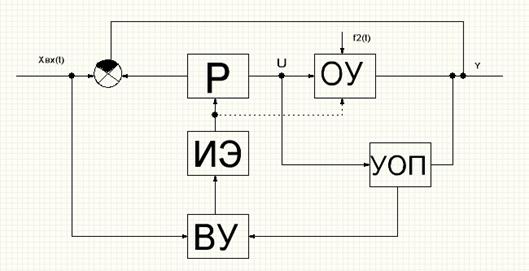
УОП – устройство определения процесса.

ВУ – вычислительное устройство.

ИЭ – исполнительный элемент.

Р – регулятор.

УОП в общем случае может определять вектор состояния объекта управления.

Классификация самонастраивающихся систем:

1) Системы изменяющие воздействие на регулятор по сигналам внешних воздействий.

2)

По динамическим характеристикам объекта.

3) Комбинированные системы

Дополнительной классификацией систем можно считать способ воздействия элементов самонастройки на систему, что позволяет системы самонастройки разделить на подклассы:

1) с автоматической настройкой параметров

2) с автоматической настройкой структуры самоорганизации системы

Кроме того системы разделяют на аналитические, поисковые с активной и пассивной настройкой.

Системы с активной настройкой параметров используются в вычислительных средствах и выполняют функцию поиска сигнала аналитически.

Системы с пассивной настройкой параметров не изменяются, а реакция производится за счёт дополнительного сигнала.

Блок-схема самонастраивающейся системы с активной и пассивной самонастройкой имеет вид:

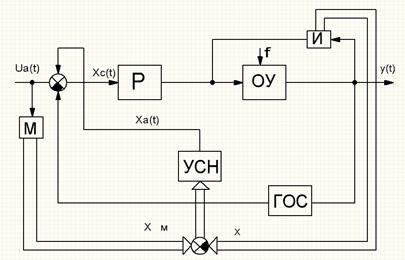
При построении самонастраивающихся систем используют эталонные модели, которые задают желаемое протекание переходных процессов.

M - эталонная модель

И - измеритель, наблюдатель

УСМ – устройство самонастройки

Р – регулятор

Ха(t) изменяет параметры регулятора (активная)

Очень часто при синтезе самонастр. использ. функция Ляпунова.

Рассмотрим пример:

Возьмём объект 1ого порядка:

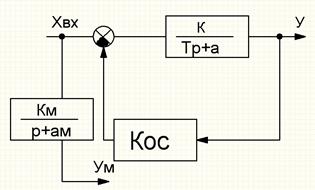
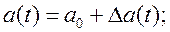
Необходимо построить параметры самонастройки для компенсации коэффициента “а”.

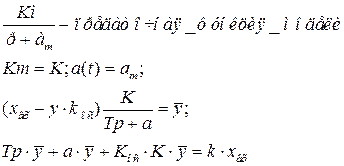
Необходимо ввести сигнал, который будет компенсировать изменение коэффициента ‘a’:

;

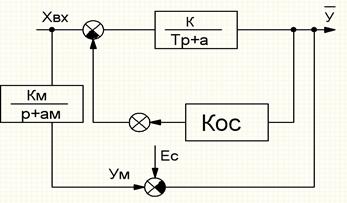
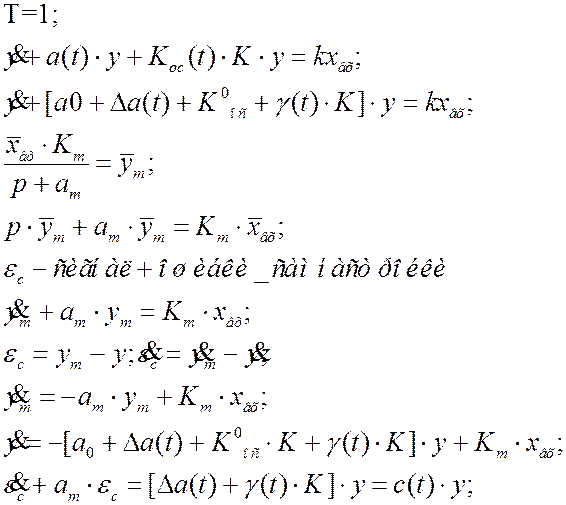
Для того чтобы система была устойчива необходимо чтобы в статике ошибка самонастройки была равна нулю.

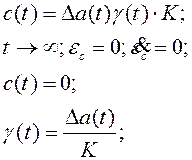
Возьмём следующую функцию Ляпунова:
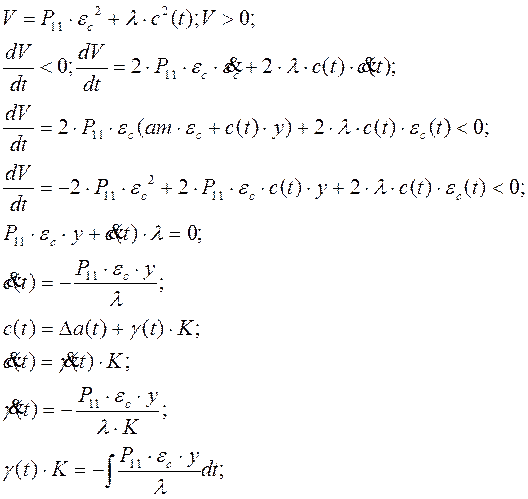