Оптимальный фильтр лчm радиоимпульса

Согласно теории оптимальной фильтрации амплитудно-частотная характеристика оптимального фильтра ЛЧМ радиоимпульса должна быть согласована с его амплитудно-частотным спектром, т.е. должна быть прямоугольной в полосе частот, равной ширине спектра сигнала Δf₀ = Δf_м, если база сигнала Δf_мТ₀ много больше единицы:

.

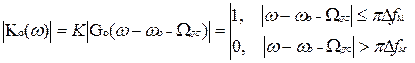Заметим, что нормирование коэффициента усиления в полосе пропускания фильтра предполагает значение К равным:

.

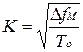Фазо-частотная характеристика оптимального фильтра должна обеспечить компенсацию фазочастотного спектра принятого сигнала и задержку в фильтре t₀:

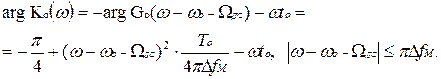
Фазо-частотная характеристика любого фильтра тесно связана с понятием задержки спектральных составляющих, осуществляемой фильтром. Задержка определяется производной от фазо-частотной характеристики фильтра по частоте:

.

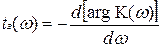В рассматриваемом случае оптимального фильтра ЛЧМ радиоимпульса

.

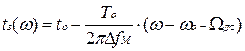Таким образом, квадратичная ФЧХ оптимального фильтра ЛЧМ радиоимпульса соответствует наличию у фильтра интересного свойства - зависимости задержки колебания от его частоты (рис. 6.8). Непостоянство времени запаздывания для различных спектральных составляющих относят к классу явлений дисперсии скорости распространения: скорость распространения колебания в среде зависит от частоты колебания. Поэтому устройства задержки с переменным временем запаздывания, зависящим от частоты колебания, называются дисперсионными.

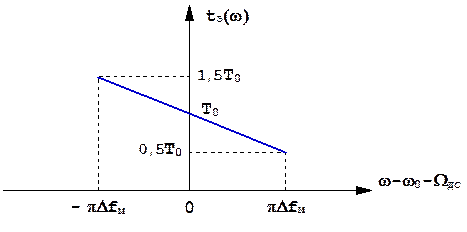
Рис. 6.8. Дисперсионная характеристика оптимального фильтра ЛЧМ радиоимпульса (t_o=T_o)

Понятие зависимости времени запаздывания от частоты колебания позволяет дать простую трактовку механизма временного сжатия при обработке ЛЧМ радиоимпульса. Устройство задержки с такой характеристикой задерживает в большей степени колебания низких частот, чем высоких. Подадим на него импульс, мгновенная частота которого изменяется от более низких вначале до более высоких частот в конце импульса (рис. 6.9). Низкие частоты действуют в данном случае ранее, но задерживаются в большей степени, а более высокие действуют позже, но задерживаются меньше. Это создает предпосылку для совмещения всех спектральных составляющих и образования сжатого импульса. Подбор оптимальной характеристики времени запаздывания эквивалентен подбору фазочастотной характеристики фильтра.

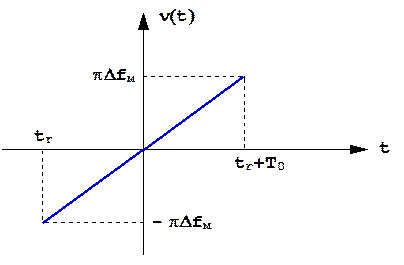
Рис. 6.9. Закон изменения частоты ЛЧМ сигнала

Дисперсия скорости распространения может быть обеспечена в линии передачи - радиоволноводе или ультразвуковом волноводе, если по крайней мере один из его размеров соизмерим с длиной волны (электромагнитного колебания или ультразвука). Различные дисперсионные задерживающие устройства имеют характеристики t_з(f) , отличающиеся рабочей полосой частот от f_min до f_max и перепадом времени задержки от t_{з min} до t_{з max} в пределах

этой полосы.

Широкое распространение в технике сжатия радиоимпульсов получили ультразвуковые волноводы. Достоинством акустических колебаний является значительно меньшая, чем у электромагнитных колебаний, скорость распространения. При сравнительно небольшие габаритах ультразвуковые волноводы позволяют получать достаточно протяженные линейные участки дисперсионной характеристики запаздывания. Поскольку желательно уменьшить затухание колебаний, ультразвуковые волноводы часто выполняются в виде металлических лент: только поперечный размер уменьшается до получения необходимой дисперсии скорости распространения ультразвука в окрестности заданной центральной частоты. Толщина ленты при этом должна быть порядка длины ультразвуковой волны в материале звукопровода.

На рис. 6.10 схематически показан пример реализации оптимального фильтра ЛЧM сигнала, состоящего из дисперсионного ультразвукового волновода с пьезоэлектрическими преобразованиями (электрических колебаний в ультразвуковые и наоборот) и усилителя с АЧХ, корректирующей амплитудно-частотные искажения в ультразвуковом волноводе, так, что результирующая АЧХ становится прямоугольной.

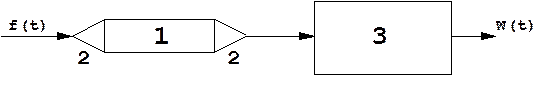
Рис. 6.10. Пример реализации оптимального фильтра ЛЧМ сигнала:
1 – дисперсионный звукопровод, 2 – пьезопреобразователи, 3 – корректирующий усилитель

Амплитуда сигнала на выходе оптимального фильтра равна:

.

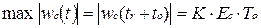С учетом нормированной АЧХ оптимального фильтра ( 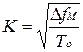) амплитуда сигнала на выходе фильтра

.

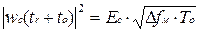Последнему результату может быть дана следующая простая интерпретация. При оптимальной фильтрации ЛЧМ радиоимпульса за счет синфазного (когерентного) сложения всех спектральных составляющих в момент t = t_r + t₀ одновременно со сжатием сигнала в Δf_мТ₀ раз происходит увеличение амплитуды сигнала в 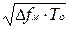раз.

Отношение сигнал/шум по мощности на выходе оптимального фильтра ЛЧМ сигнала определяется как всегда отношением энергии сигнала к спектральной плотности шума:

.
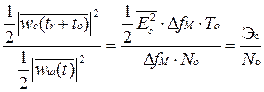