Модель идеального газа

Молекулярно-кинетическая теория рассматривает модель идеального газа, удовлетворяющую следующим условиям:

1) размеры молекул пренебрежимо малы, их принимают за материальные точки;

2) не учитываются силы взаимодействия между молекулами;

3) столкновение молекул друг с другом и со стенками сосуда считаются абсолютно упругими.

Этим условиям удовлетворяют обычные газы при невысоких давлениях и температурах(например, воздух в комнате).

Состояние некоторой массы газа определяется значением основных параметров:

Р – давление, в СИ – системе измеряется в Па;

V – объем, в СИ – системе измеряется в м³;

Т – температура, в СИ измеряется в Кельвинах. Температура – физическая величина, характеризующая состояние термодинамического равновесия системы, обусловленная движением молекул.

Соотношения, устанавливающие связь между параметрами, называются уравнениями состояния.

Поведение идеальных газов описывается рядом законов, являющихся обобщением экспериментальных данных:

1. Закон Авогадро: моли любых газов при одинаковых температурах и давлениях занимают одинаковые объемы (моль – это такое количество вещества, масса которого численно равна его молекулярной массе). При нормальных условиях (Р=1,013333·10⁵ Па, Т=273,15 К) объем моля равен 22,4·10^{-3 м3}.

По определению в одном моле различных веществ содержится одинаковое количество молекул, называемое числом Авогадро:

N_А=6,022·10²³ моль^-1.

2. Закон Дальтона: давление смеси идеальныхгазов равно сумме парциальных давлений газов, входящих в состав смеси:

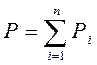
Здесь Р_i – парциальное давление, т.е. давление, которое оказывал бы один из газов смеси, если бы он один занимал весь объем, в котором находится смесь.

3. Уравнение Менделеева – Клапейрона, или уравнение состояния, связывающее между собой параметры идеального газа:

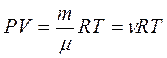(2.1)

Здесь m – масса газа; μ – его молярная масса, 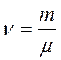- число молей, R = 8,31 Дж/(моль · К) – универсальная газовая постоянная. Молярная масса равна массе одного моля вещества, т.е. определяется произведением числа Авогадро N_A и массы частицы вещества.

Из формулы (2.1) можно выразить плотность веществ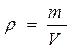а газа:

.
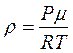