Границы применимости закона Максвелла распределения молекул газа по скоростям

ЛАБОРАТОРНАЯ РАБОТА №6

Изучение распределения молекул идеального газа по скоростям

Цель работы: познакомиться со статистическим методом описания системы многих частиц; проверить экспериментально на модели закон Максвелла для двумерного случая.

КРАТКОЕ ТЕОРЕТИЧЕСКОЕ СОДЕРЖАНИЕ

Молекулярная физика изучает системы, состоящие из очень большого числа частиц. Наиболее простой моделью системы многих частиц является идеальный газ. Эта система состоит из большого числа точечных материальных объектов с конечной массой, находящихся в состоянии непрерывного хаотичного движения. Частицы не взаимодействуют друг с другом на расстоянии. При столкновении ведут себя как упругие шары. Наиболее близко свойствам идеального газа соответствуют обычные газы при условиях, не сильно отличающихся от нормальных. Простота модели идеального газа делает ее удобной для ознакомления с методами систем многих частиц. Различают три метода описания систем: динамический, термодинамический, статистический.

Динамический метод.

Поведение каждой молекулы идеального газа подчиняется механическим законам движения и взаимодействия (если не учитывать волновых свойств молекул, что вполне допустимо для идеального газа). Естественно было ожидать, что и свойства всей системы должны следовать тем же механическим законам.

Основной особенностью механических законов является их детерминированность, т.е. полная причинная обусловленность процессов. Так, например, второй закон Ньютона является строго детерминированным законом. Это проявляется в следующем: если известно выражение для силы, действующей на частицу, то значения ее координат и скорости в начальный момент времени полностью определяют траекторию ее движения, т.е. значения координат и скорости в любой момент времени. Всё последующее поведение частиц обусловлено (является следствием) начальными условиями. Способ описания системы, когда в любой момент времени известны координаты и скорости всех частиц ее составляющих, называется динамическим. Он успешно применяется для описания систем, состоящих из небольшого числа частиц (например, для Солнечной системы). Применение динамического способа описания к идеальному газу, сводилось бы к определению координат и скоростей всех его молекул (2,7×10¹⁹ в 1 см³) в какой-то момент времени. Эта задача в настоящее время является технически невыполнимой. Но не в этом заключается принципиальная невозможность применения динамического способа описания к молекулярным системам.

Оказывается, что полная информация о значениях координат и скоростей всех частиц в какой-то момент времени является бесполезной и не может быть использована для теоретического анализа поведения системы в целом. Дело в том, что молекулы газа при нормальных условиях испытывают примерно 10⁹ столкновений в секунду, при которых происходит изменение скоростей молекул. Поэтому система, состоящая из большого числа частиц, очень скоро «забывает» свое начальное состояние. Кроме того, динамический способ описания поведения системы позволяет ей вернуться самостоятельно без внешнего воздействия в первоначальное состояние. Например, газ расширился и занял большой объем. С динамической точки зрения ничто не мешает ему самопроизвольно сжаться до первоначального объема. Однако самопроизвольного сжатия еще никогда не наблюдалось. Все это указывает на то, что для описания молекулярной системы, состоящей из очень большого числа частиц, следует искать другие методы описания.

Термодинамический метод.

Систему многих частиц можно рассматривать, не интересуясь ее внутренней структурой и характером движения частиц. При таком подходе используют характеристики, относящиеся ко всей системе в целом. Например, идеальный газ в состоянии равновесия характеризуется объемом, давлением и температурой. Эти характеристики относятся к системе в целом и называются макроскопическими.

Экспериментальные исследования устанавливают связь между этими величинами (уравнение состояния). Теория строится на основании общих законов (три начала термодинамики). Такой метод изучения систем многих частиц называется термодинамическим. Он характеризуется своей общностью и позволяет изучать явления без знания их внутренних механизмов. Термодинамический метод успешно применяется при изучении сложных систем.

Статистический метод.

Статистический метод описания в известной степени является обобщением двух предыдущих: динамического и термодинамического. В его основе лежат следующие представления:

- свойства системы в целом определяются свойствами и характером движения частиц, ее составляющих;

- в силу многочисленности частиц и большого числа столкновений их поведение носит случайный характер;

- поведение системы в целом необходимо описывать не совокупностью координат и скоростей частиц, а усредненными характеристиками (средняя энергия, средняя плотность и т.д.). При сопоставлении этих усредненных характеристик с термодинамическими соотношениями выясняется смысл микроскопических параметров системы. Так, например, оказалось, что абсолютная температура пропорциональна средней кинетической энергии поступательного движения молекул.

Закономерности, получаемые статистическим методом, называются вероятностными, или статистическими. Для их получения строится модель изучаемой системы.

Статистический метод в физике имеет широкое применение по двум причинам:

- большинство физических систем имеют огромное число частиц;

- поведение микрочастиц описывается статистическими закономерностями.

В данной работе рассматривается применение статистического метода описания к вопросу о распределении молекул газа по скоростям в состоянии равновесия, в отсутствие внешних силовых полей. Опыт показывает, что любая изолированная система приходит в состояние теплового (термодинамического) равновесия, в котором ее макроскопические параметры (давление, температура) не изменяются со временем и постоянны в объеме. Но согласно основным представлениям молекулярно-кинетической теории молекулы системы находятся в беспорядочном хаотическом движении. В идеальном газе молекулы движутся между столкновениями поступательно с разными скоростями, изменяя скорость при столкновении. В этом случае случайной величиной (разной у молекул) является скорость и стоит задача о нахождении распределения молекул газа по скоростям. Для этого необходимо принять модель системы и качественно рассмотреть свойства этой системы в состоянии теплового равновесия.

Так как в состоянии равновесия давление во всех частях системы одинаково, то естественно допустить, что в газе отсутствуют какие-либо направленные движения молекул, то есть движения молекул предельно неупорядочены. В отношении скоростей молекулы это означает:

- скорость молекул и ее проекции являются непрерывными величинами, так как ни одно значение скорости не имеет преимущества перед другими значениями;

- при тепловом равновесии в газе все направления скоростей молекул равновероятны. В противном случае это привело бы к образованию направленных макроскопических потоков молекул и возникновению перепадов давления.

Так как скорость и ее проекции являются непрерывными величинами, вводится понятие функции плотности распределения f(v_x), f(v_y), f(v_z) по компонентам скоростей молекул (v_x, v_y, v_z) и по модулю скорости f(v)

.

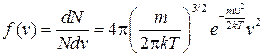Выражения для функций плотности вероятности по компонентам скоростей v_x, v_y, v_z имеют вид

;

.

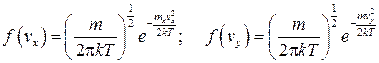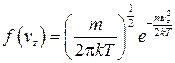График функции f(v_x)изображен на рис. 1.

Функция имеет максимум при v_x = 0, симметрична относительно его и экспоненциально стремится к нулю при v_x ® ± ¥. Отложим по оси абсцисс элементарные скоростные интервалы dv_x около значений v_x, равных 0; ± v_x¢; ± v_x¢¢. Произведение f(v_x) dv_x равно доле молекул, компонента скорости v_x которых лежит в интервале около указанных значений. С другой стороны, произведение f(v_x) dv_x на графике равно заштрихованным площадкам около выбранных скоростей.

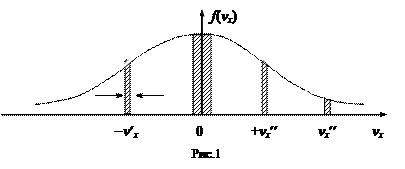Из сопоставления размеров заштрихованных площадей следует:

- относительное большинство молекул имеет проекцию скорости вдоль оси v_x, близкую к нулю;

- доли молекул, имеющих одинаковые значения v_x, но летящие в противоположных направлениях (разные знаки +v_x и -v_x), одинаковы;

- число молекул, имеющих большие значения компонент скоростей, мало (мала площадь около ± v_x¢¢).

Аналогичный анализ можно провести и для f(v_y), f(v_z).

График функции f(v) изображен на рис. 2.

Функция равна 0 при v = 0; стремится к нулю при v ® ¥, при v = v_вер имеет максимум. Значение скорости v_вер, при которой функция плотности распределения достигает максимума, называется наиболее вероятной скоростью. Ее значение находится из условия экстремума.

.

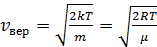Произведение f(v) dv дает долю молекул, скорости которых лежат в выбранном интервале dv. На графике это произведение равно заштрихованным площадкам. Как видно из графика, максимальная площадка соответствует скорости v_b. С увеличением скорости доля молекул, обладающих большими скоростями, уменьшается (малая площадь при v₃). Зная аналитический вид f(v), можно найти <v>

;

.

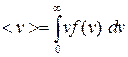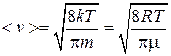Распределение молекул по скоростям зависит от температуры.

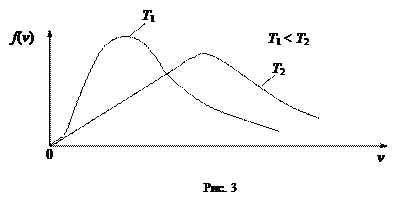На рис. 3 приведены кривые распределения молекул по скоростям при разных температурах. При повышении температуры наиболее вероятная скорость увеличивается, поэтому максимум кривой смещается в сторону больших скоростей. Площади, ограниченные кривыми и осью скоростей, равны единице и не могут измениться при повышении температуры. Вследствие этого максимум понижается по мере повышения температуры и становится менее острым.

Закон Максвелла распределения молекул газа по скоростям описывает поведение очень большого числа частиц, то есть является статистическим законом. Распределение молекул по скоростям устанавливается посредством их столкновений. При столкновениях изменяются скорости отдельных молекул, но закон распределения по скоростям не изменяется.

Эту ситуацию можно понять следующим образом. Выделим среди молекул несколько скоростных групп, то есть групп молекул, скорости которых лежат в интервале dv около значений v_x, v_y, v_z и так далее. Количество молекул в этих скоростных группах обозначим, соответственно, через dN₁, dN₂, dN₃ и т.д. При столкновении молекулы изменяют свою скорость и выбывают из своей скоростной группы в другую. Точно такое же количество молекул переходит в эту скоростную группу из других групп, так что в любой момент времени в состоянии теплового равновесия число молекул в каждой скоростной группе неизменно. Итак, за большой промежуток времени молекула, изменяя скорость при столкновениях, «переберет» все значения скоростей от малых до больших.

Границы применимости закона Максвелла распределения молекул газа по скоростям

Задача о распределении молекул газа по скоростям, как она сформулирована и решена выше, является чисто классической. Необходимо выяснить границы применимости такого классического рассмотрения.

В квантовой механике показано, что поведение частиц можно описывать законами классической физики, если nl³ << 1, где l - длина волны де Бройля частицы (l=h / mv); n – плотность частиц. Для оценки порядка l воспользуемся среднеквадратичной скоростью молекул 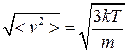. Используя ее, имеем

.

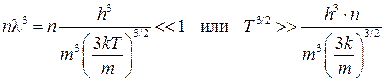Извлекая корень степени 3/2, имеем .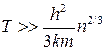

При более точном рассмотрении вместо этого соотношения получается неравенство

.

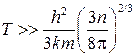Величина

(*)

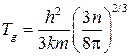называется температурой вырождения. Следовательно, классический закон Максвелла имеет место, если температура газа много больше температуры вырождения.

Вычислим температуру вырождения по формуле (*) для двух случаев. Для электронного газа в серебре n » 6×10²² см^-3, масса электрона m = 9,1×10^-31 Кл. Температура вырождения газа в серебре Т_g = 6,5×10⁴ К. Подобные значения получаются для всех других хорошо проводящих металлов. При таких высоких температурах ни один металл в твердом состоянии существовать не может. Следовательно, электронный газ в проводящем металле всегда находится в состоянии вырождения и распределение электронов проводимости по скоростям не подчиняется закону Максвелла. Это, разумеется, не означает, что в любом количестве электронов распределение Максвелла по скоростям не имеет место. Все определяется свойствами системы в целом. Так, например, в «электронном» облаке, образовавшемся около металла вследствие термоэлектронной эмиссии, электроны распределены по скоростям по закону Максвелла.

Теперь вычислим температуру вырождения для газообразного гелия. Масса атома гелия m = 6,6×10^-27 кг, концентрация при нормальных условиях n = 2,7×10²⁵ м^-3. Температура вырождения Т_g @ 0,5 К. У всех остальных газов масса атома еще больше (кроме водорода), а Т_g еще меньше. Следовательно, все молекулярные газы достаточно далеки от вырождения и закон распределения Максвелла молекул газа по скоростям для них имеет место.