Принцип нерозрізненості тотожних частинок. Принцип Паулі
До цих пір ми розглядали рух лише однієї квантової частинки. Незвичайні, із класичної точки зору, властивості проявляються при вивченні руху системи квантових частинок. Квантова теорія систем частинок полягає в тому, що в цій теорії поняття хвильової функції відноситься лише до системи частинок. Кожна окрема частинка системи не знаходиться в певному квантовому стані і не може бути охарактеризована своєю хвильовою функцією, яка б залежала лише від параметрів даної частинки.
Система квантових частинок набуває властивостей, яким не має аналога ні в класичній фізиці ні у квантовій механіці однієї частинки. Специфічна особливість квантової теорії систем частинок полягає в їх принциповій нерозрізненості. Усі частинки такої квантової системи є тотожними.
Нерозрізненість тотожних частинок в квантових системах не властива для систем класичних частинок, де кожна частинка системи має свою індивідуальність.
У квантовій фізиці однакові частинки втрачають свою індивідуальність, тому що вони рухаються не по траєкторіях. Поняття траєкторії квантових частинок через наявність хвильових властивостей втрачає будь-який фізичний зміст.
Із принципової нерозрізненості однакових частинок випливає, що перестановка місцями двох однакових частинок в системі не впливає ні на одну з фізичних величин, що характеризують цю систему.
Слід відмітити, що при перестановці місцями двох частинок в системі хвильова функція, яка є функцією всіх параметрів частинок цієї системи, змінюється з Y на Y1. Однак густина імовірності при цьому не змінюється, тобто
|Y|2=|Y1|2.
В той же час хвильова функція Y1 відрізняється від Y на множник eia, де a ― деяка дійсна величина. Переставимо ті ж частинки ще раз місцями, тобто повернемось в попередній стан, густина імовірностей знову ж не зміниться, а от хвильова функція Y буде відрізнятись від Y в початковий момент на е2іa . Для рівності імовірностей необхідно, щоб е2іa =1, а еіa = ± 1. З цих міркувань видно, що при перестановці місцями довільної пари частинок системи хвильова функція може залишитися такою ж, або змінювати знак.
Хвильова функція, яка при перестановці місцями двох частинок системи не змінює свого знаку ― називається симетричною. В тих випадках, коли при аналогічній перестановці частинок системи хвильова функція змінює знак, вона є антисиметричною.
Симетрія хвильової функції системи однакових частинок зберігається з часом. Тому тип симетрії хвильової функції є властивістю тільки самих частинок.
Системи однакових частинок із нульовими, або цілочисловими спінами описуються лише симетричними хвильовими функціями і називаються бозонами.
Системи однакових частинок із напівцілими спінами описуються лише антисиметричними хвильовими функціями і називаються ферміонами.
До ферміонів відносяться електрони ( 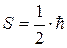 ), протони і нейтрони (
), протони і нейтрони ( 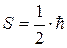 ) й інші частинки.
) й інші частинки.
До бозонів відносяться p-мезони ( 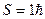 ), фотони (
), фотони ( 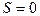 ) і інші частинки.
) і інші частинки.
Спін мікроскопічної частинки є її найважливішою характеристикою. Так від спінів частинок залежать статистичні властивості квантових систем, які складаються з багатьох частинок. Статистичні властивості частинок із нульовими й цілочисловими спінами вперше вивчали Бозе й Ейнштейн ще в 1924 році, від чого відповідна квантова статистика дістала назву статистики Бозе-Ейнштейна. Статистичні властивості частинок із напівцілими спінами вивчали в 1926 році Фермі і Дірак ― звідки назва відповідної квантової статистики Фермі-Дірака.
Зупинимось на розподілі електронів в атомі на відповідних енергетичних рівнях. Відомо, що стан кожного з електронів можна характеризувати чотирма квантовими числами: n, l, ml, ms, де n ― головне квантове число, яке квантує енергію електрона в атомі і визначає розміри орбіти електрона; l ― орбітальне квантове число, що визначає (квантує) орбітальний момент імпульсу (механічний момент); ml ― магнетне квантове число, квантує проекцію вектора механічного моменту на заданий напрям зовнішнього магнетного поля; ms ― спінове квантове число, що визначає орієнтацію власного механічного і магнетного моментів електрона.
За принципом Паулі (1924 р.) електрони, які входять до складу якої-небудь системи, зокрема електрони атомних оболонок, не можуть перебувати в тотожних станах руху. Інакше кажучи, в будь-якому стаціонарному стані, що характеризується сукупністю чотирьох квантових чисел n, l, ml, ms, не може перебувати більше одного електрона.
Принцип Паулі має використання лише для систем частинок з антисиметричними хвильовими функціями, тобто до ферміонів.
