Теоретическая часть. Методические указания к лабораторной работе №19
ОПРЕДЕЛЕНИЕ ИНДУКТИВНОСТИ КАТУШКИ
Методические указания к лабораторной работе №19
по физике
(Раздел «Электричество и магнетизм»)
Ростов-на-Дону
УДК 530.1
Составители: В.С. Ковалева, Н.Н. Фролова
Определение индуктивности катушки: метод. указания к лабораторной работе №19 по физике. – Ростов н/Д: Издательский центр ДГТУ, 2012. – 11 с.
Указания содержат краткую теорию переменного тока в цепи, содержащую катушку индуктивности, и методику определения индуктивности катушки методом вольтамперметра.
Методические указания предназначены для студентов инженерных специальностей всех форм обучения, в программу учебного курса которых входит выполнение лабораторных работ по физике (раздел «Электричество и магнетизм»).
Печатается по решению методической комиссии факультета
«Нанотехнологии и композиционные материалы»
Рецензент д-р. техн. наук, проф. В.С. Кунаков
©Издательский центр ДГТУ, 2012
ОПРЕДЕЛЕНИЕ ИНДУКТИВНОСТИ КАТУШКИ
Цель работы: 1) определить индуктивность катушки;
2) исследовать зависимость индуктивности катушки от силы тока при наличии в катушке стального сердечника.
Оборудование: источники постоянного и переменного тока, амперметр, вольтметр, реостат, ключ, катушка индуктивности, соединительные провода, стальной сердечник.
Теоретическая часть
Явление возникновения электродвижущей силы (ЭДС) в замкнутом проводящем контуре при изменении магнитного потока в нем называется электромагнитной индукцией.
Электрический ток, появляющийся в этом случае, называется индукционным.
Направление индукционного тока определяется по правилу Ленца:
Индукционный ток всегда направлен так, что его магнитное поле противодействует изменению магнитного потока, вызвавшего появление данного тока.
Возникновение ЭДС индукции в электрической цепи вследствие изменения в ней силы тока называется самоиндукцией.
ЭДС самоиндукции пропорциональна скорости изменения силы тока в контуре
. (1)
Коэффициент пропорциональности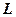 
называется индуктивностью и измеряется в генри (Гн). Индуктивность контура является мерой его "инертности" по отношению к изменению силы тока в нем и зависит от размеров и формы контура, а также от магнитной проницаемости 
окружающей среды.
Реальная катушка, обладающая активным сопротивлением 
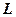и индуктивностью , в цепи переменного тока соответствует последовательно включенным и 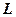. Рассмотрим цепь переменного тока, содержащую последовательно соединенные активное сопротивление и катушку индуктивности 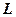(рис. 1).
Пусть ток в цепи изменяется по гармоническому закону
, (2)
где 
- амплитудное значение силы тока, 
циклическая частота переменного тока.
Напряжение на резисторе определяется законом Ома
, (3)
где 
– амплитудное значение напряжения на резисторе. Сравнивая (2) и (3), заключаем, что напряжение и сила тока на резисторе изменяются в одинаковой фазе (синфазно).
При протекании переменного тока через катушку индуктивности 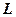в ней возникнет ЭДС самоиндукции, определяемая выражением (1). Тогда закон Ома для участка цепи, содержащего катушку 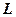, будет иметь вид:
,
где 
– напряжение на катушке индуктивности.
Отсюда имеем
и, учитывая (2), получаем
, (4)
где 
– амплитудное значение напряжения на катушке,
а 
называют реактивным индуктивным сопротивлением.
Сравнивая (2) и (4), заключаем, что напряжение на катушке индуктивности опережает ток на 
.
Общее напряжение на участке - 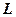цепи имеет вид:
.
Соотношения между переменными токами и напряжениями делаются особенно наглядными, если изображать их с помощью векторов.
Выберем ось токов и отложим на ней амплитудное значение силы тока. Тогда амплитудные значения напряжений 
и 
расположатся так, как показано на рис.2. Из диаграммы следует, что:
,
или
,
где 
- амплитудное значение результирующего напряжения.
Откуда амплитуда силы тока имеет значение
.
Величина
(5)
называется полным сопротивлением цепи катушки и активного сопротивления. Угол 
дает разность фаз между напряжением 
и силой тока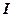 
.
Из выражения (5) получаем индуктивность катушки
, (6)
где 
=50 Гц – частота переменного тока.