Определение емкости конденсатора
Электричество и магнетизм
Руководство к лабораторным работам
Учебно-методическое пособие
Направления подготовки:
140400.62 Электроэнергетика и электротехника
140100.62 Теплоэнергетика и теплотехника
150400.62 Металлургия
190109.65 Наземные транспортно-технологические средства
190600.62 Эксплуатация транспортно-технологических машин и комплексов
Череповец
Рассмотрено на заседании кафедры физики, протокол № 3 от 17.09.13 г.
Одобрено учебно-методической комиссией Института информационных технологий ЧГУ, протокол № 2 от 03.10.13 г.
Составители: H.О. Сорокина – канд. физ.-мат. наук, доцент,
Т.О. Петрова – канд. физ.-мат. наук
Рецензенты: О.Г. Максимова – канд. физ.-мат. наук, доцент (ЧГУ);
С.С. Шевченко – канд. физ.-мат. наук, доцент (ЧВВИУРЭ)
Научный редактор: А.В. Максимов– д-р физ.-мат. наук, проф.
© Сорокина Н.О., Петрова Т.О., 2014
| |
Введение
Лабораторный практикум является неотъемлемой частью курса физики. В данном методическом пособии в достаточном объеме приводятся теоретические сведения по темам предложенных лабораторных работ из раздела «Электричество и магнетизм» и подробное описание порядка их выполнения и расчета. В пособие включены все необходимые таблицы. Надеемся, что это поможет успешному освоению курса студентами всех специальностей.
Лабораторная работа 1(2)
ИССЛЕДОВАНИЕ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ
Цель работы:исследовать электростатическое поле и описать его с помощью эквипотенциальных поверхностей и линий напряженности; рассчитать напряженность поля.
Теоретическая часть
Электростатическое поле характеризуется в каждой точке пространства значениемвектора напряженности и потенциала 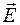 и φ. Линия, касательная к которой в каждой точке направлена вдоль вектора напряженности в этой точке, называется линией напряженности (силовой линией, поскольку вектор
и φ. Линия, касательная к которой в каждой точке направлена вдоль вектора напряженности в этой точке, называется линией напряженности (силовой линией, поскольку вектор 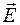 определяется силой, действующей на единичный пробный заряд, помещенный в данную точку).
определяется силой, действующей на единичный пробный заряд, помещенный в данную точку).
Знание потенциала в каждой точке φ (х, у, z) позволяет определить эквипотенциальную поверхность φ (х, у, z) = const. Причем поскольку потенциал – есть энергетическая характеристика электрического поля, то при перемещении электрического заряда по эквипотенциальной поверхности над ним не совершается полем работа. Это позволяет сделать вывод об ортогональности линий напряженности к эквипотенциальным поверхностям.
Обычно экспериментально изучается распределение потенциала в поле, проводятся эквипотенциальные поверхности, а затем ортогонально к ним наносится картина силовых линий.
Изучение электростатического поля в диэлектрической среде затруднительно. Использование обычных вольтметров, потребляющих ток, невозможно, так как при этом искажается вся картина электростатического поля.
Выход состоит в создании электрического поля в слабопроводящей среде. Электрическое поле при наличии постоянных токов по-прежнему остается потенциальным и удовлетворяет тем же уравнениям. Скалярный потенциал подчиняется уравнению Пуассона с определенными граничными условиями на поверхностях проводников. Если поверхности проводников, находящихся в проводящей среде, и при наличии тока остаются эквипотенциальными (это возможно, если удельная проводимость проводника много больше проводимости среды), то электрическое поле в проводящей среде является таким же, как и в диэлектрической. Разумеется, распределение потенциалов на проводниках в первом и во втором случаях должно быть одинаковым. Подключение вольтметра, потребляющего ток, много меньший по сравнению с током, текущим в среде, не исказит распределение тока, силовых линий и потенциала. Более подробно см. [1].
Пользуясь методом моделирования, изучают сложные электростатические поля (в электростатических линзах, электронных лампах). При этом широко пользуются правилом подобия, которое утверждает, что если размеры электродов и все расстояния между этими электродами изменить в одной пропорции, то картина силовых линий и эквипотенциальных поверхностей останется прежней [1].
В работе предлагается один из способов моделирования электростатического поля. Проводники А и В (рис. 1) опускают в тонкий слой воды (3–4 мм), налитой в сосуд из непроводящего материала. Вода имеет незначительную проводимость по сравнению с металлом, поэтому поверхности металлических электродов с хорошей точностью можно считать эквипотенциальными.
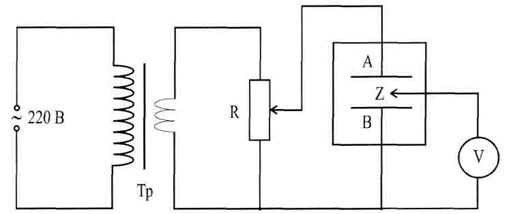
Рис. 1. Установка для моделирования.
ТР – трансформатор 220x12В; R – реостат; А и В – электроды,
помещенные в ванну для моделирования; V – ламповый вольтметр;
Z – зонд
Практически очень удобно работать с переменным напряжением. Если скорость изменения напряжения мала (низкая частота), то можно считать поле в каждый момент времени электростатическим при условии пренебрежения эффектами электромагнитной индукции.
Электроды присоединяются к источнику небольшого переменного напряжения и вольтметром V измеряют напряжение между одним из электродов и исследуемой точкой поля, поместив в эту точку зонд Z. Поскольку в данном случае исследуется электростатическое поле в плоскости поверхности воды, то находятся линии пересечения эквипотенциальных поверхностей с горизонтальной плоскостью. Для нахождения этих линий отмечают ряд положений зонда, соответствующих одному и тому же показанию вольтметра. Соединяя эти точки между собой, находят форму следа эквипотенциальной поверхности.
Для определения разности потенциалов между одним из электродов и исследуемой точкой поля пользуются ламповым вольтметром, который потребляет ничтожный ток и обладает сопротивлением, очень большим по сравнению с сопротивлением проводящих слоев воды между исследуемой точкой и электродом. Простейшая схема лампового вольтметра приведена на рис. 2. Электронные лампы, входящие в состав лампового вольтметра, нуждаются в источнике накала и анодного напряжения. Поэтому перед началом измерений ламповый вольтметр необходимо включить в сеть и дать прогреться.
Перед началом измерений необходимо установить одинаковыми потенциалы точек 1 и 2, что достигается изменением положения движка потенциометра (на шкале прибора ручка с надписью «Установка 0»). Чтобы исключить действие на вход паразитных ЭДС, щупы вольтметра при этом необходимо закоротить.
Для изменения пределов измерений имеется переключатель.
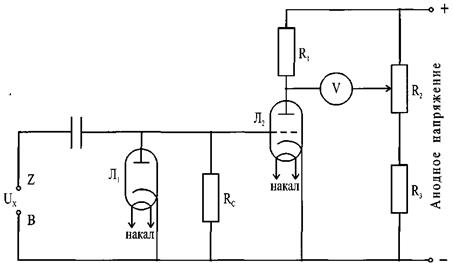
Рис. 2. Схема лампового вольтметра
Экспериментальная часть
Приборы и принадлежности:
1) плоский сосуд-ванна для моделирования;
2) набор электродов;
3) зонд;
4) ламповый вольтметр;
5) понижающий трансформатор 220 на 12 В;
6) реостат на 40–100 Ом;
7) уровень;
8) миллиметровая бумага.
Порядок выполнения работы
Задание 1. Исследование модели электростатического поля между плоскими пластинами (модель поля конденсатора).
1. Собрать приборы по схеме (рис. 1). Переключатель шкал лампового вольтметра поставить так, чтобы предельное напряжение, измеряемое вольтметром, было близко к напряжению, снимаемому с понижающего трансформатора Тр.
2. Положить зонд на электрод В и установить стрелку лампового вольтметра на нуль. Перенести зонд на электрод А и реостатом R установить для удобства разность потенциалов, равную целому числу вольт. Плоские электроды расположить параллельно друг другу на расстоянии, меньшем их длины в несколько раз.
3. Нанести на миллиметровой бумаге (в масштабе 1:1) положение электродов. Исследуя поле, необходимо следить за постоянством напряжения. Поскольку в данном упражнении имеется симметрия, предлагается изучить поле в области, ограниченной пунктирным прямоугольником (рис. 3).
4. Опустить зонд вертикально в электролит, заметить показания вольтметра (удобно взять точку с потенциалом в целое число вольт) и передвигать зонд так, чтобы показания вольтметра не менялись. Отдельные положения зонда фиксировать и сразу отмечать на листе миллиметровой бумаги (не менее 8–10 точек). Показания вольтметра отметить. При выполнении работы зонд держать за изолированную ручку. Положение зонда и электродов отсчитывать по миллиметровой координатной сетке, помещенной под дном сосуда.
5. Точки, соответствующие одинаковому потенциалу, соединить линией. Провести не менее 4 линий, соответствующих следам эквипотенциальных поверхностей. Около каждой линии написать потенциал, которому она соответствует.
6. Нанести силовые линии.
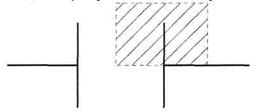
Рис. 3. Поле между плоскими пластинами
7. Сравнить полученное изображение поля с известным, результат сравнения привести в конце отчета и сделать вывод.
Задание 2. Исследование модели поля около проводника, помещенного в однородное поле (рис. 4).
1. Проделать то же, что и в первом случае, поместив между электродами металлический цилиндр. Особенно тщательно измерить поле вблизи цилиндра. Убедиться, что потенциал на оси симметрии системы совпадает с потенциалом цилиндра.
2. Провести линии напряженности, перпендикулярные следам эквипотенциальных поверхностей.
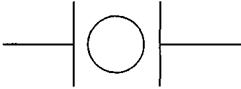
Рис. 4. Проводник в электрическом поле
Задание 3. Исследование модели поля коаксиальных заряженных цилиндров (рис. 5).
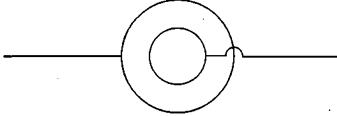
Рис. 5. Поле коаксиальных заряженных цилиндров
Контрольные вопросы и задания
1. Рассчитайте напряженность поля в двух–трех точках для каждого задания по формуле 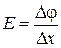 .
.
2. Рассчитайте модуль поверхностной плотности заряда в модели задания 1.
3. Рассчитайте напряженность модельного поля около внутреннего и наружного цилиндров в задании 3 и сравните с формулой 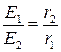 .
.
4. Что называется:
а) напряженностью электрического поля в данной точке;
б) линиями напряженности?
5. Дайтеопределение:
а) потенциала в данной точке;
б) эквипотенциальной поверхности.
6. Какая связь между напряженностью и потенциалом?
7. Какова взаимная ориентация линий напряженности и эквипотенциальных поверхностей? Объясните.
8. Какое электрическое поле называется однородным? Приведите пример.
9. Чему равна напряженность поля, создаваемого:
а) равномерно заряженной плоскостью;
б) равномерно заряженным по поверхности цилиндром;
с) равномерно заряженной по поверхности сферой?
10. Докажите соотношения:
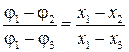 – для однородного поля;
– для однородного поля;
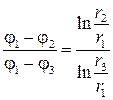 – для поля цилиндрического конденсатора.
– для поля цилиндрического конденсатора.
Лабораторная работа 2(3)
ОПРЕДЕЛЕНИЕ ЕМКОСТИ КОНДЕНСАТОРА
МЕТОДОМ МОСТИКА
Цель работы: ознакомиться с методом измерения емкости конденсаторов при помощи мостика и экспериментально подтвердить формулы параллельного и последовательного соединения конденсаторов.
Теоретическая часть
Измерения, проводимые в работе, основаны на свойствах конденсаторов в цепи переменного тока. Постоянный ток не может идти через конденсатор, т. к. диэлектрик между пластинами конденсатора (воздух, слюда и др.) разрывает электрическую цепь. Однако в течение некоторого промежутка времени после замыкания цепи в ней протекает ток, заряжающий конденсатор. Этот ток быстро убывает по мере того, как разность потенциалов на обкладках конденсатора приближается к электродвижущей силе источника. Если источник постоянного тока заменить генератором переменного тока, то конденсатор будет непрерывно перезаряжаться и в цепи будет идти переменный ток. На схемах, изображенных на рис. 6 и 7, легко продемонстрировать отсутствие тока в цепи постоянной ЭДС и прохождение тока через конденсатор в цепи переменной ЭДС. На рис. 6 лампочка через конденсатор присоединена к батарее аккумуляторов (общее напряжение их 220 В). При этом лампочка не горит. На рис. 7 та же лампочка присоединена через конденсатор к источнику переменного тока напряжением 220 В и светится.

Рис. 6. Схема опыта, демонстрирующего отсутствие
постоянного тока в цепи с конденсатором

Рис. 7. Схема опыта, демонстрирующего прохождение
переменного тока через конденсатор
В данной работе и используется способность переменного тока проходить через конденсатор.
Рассмотрим схему на рис. 8 (мостик Уитсона).

Рис. 8. Мостик Уитсона
Переменный ток проходит по двум параллельным ветвям. Одна из них состоит из двух последовательно соединенных конденсаторов с емкостями С1 и С2, другая – из двух последовательно соединенных сопротивлений R1 и R2. Разность потенциалов на концах обеих ветвей одинакова jА – jВ (индекс у обозначения потенциала соответствует точке, к которой данный потенциал относится). Распределение потенциалов между емкостями и сопротивлениями нетрудно найти.
Для конденсаторов, включенных последовательно, величины зарядов на пластинах (по модулю) одинаковы, поэтому из равенства
q = C1(jA – jМ) = C2(jМ – jB)
находим
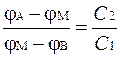 . (1)
. (1)
В ветвях сопротивлений общий ток I по закону Ома
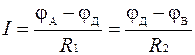 ,
,
откуда
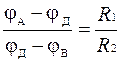 . (2)
. (2)
Потенциалы точек М и Д – промежуточные между jА и jВ. Путем подбора сопротивлений R1 и R2 или емкостей можно добиться, чтобы jМ = jД. Существование равенства потенциалов легко установить, если перебросить между точками М и Д «мостик», т.е. соединить их друг с другом. При jМ = jД тока в соединительном мостике не будет, что можно установить соответствующим прибором. Если jМ = jД, то
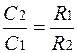 .
.
При выводе формулы используется равенство левых частей уравнений (1) и (2). Если известны оба сопротивления и одна из емкостей, то можно найти другую емкость.
Рабочая схема приведена на рис. 9. В качестве сопротивлений R1 и R2 используется реохорд, представляющий собой калиброванную проволоку, натянутую на 50-сантиметровую линейку.

Рис. 9. Схема экспериментальной установки для определения
емкости конденсаторов методом мостика Уитсона. С1 – магазин емкостей
По реохорду скользит движок Д, часть АД калиброванной проволоки, длиной l1, включается в схему как R1, а ее часть ДВ, длиной l2, включается как R2. Поскольку сопротивление проволоки пропорционально ее длине (при неизменном поперечном сечении)
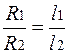 ,
,
то сразу получаем
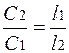
или
 . (3)
. (3)
В качестве емкости С1 берется магазин емкостей, т.е. набор конденсаторов известной емкости, а в качестве С2 берется емкость, которую требуется измерить. Условием справедливости формулы (3) является отсутствие тока в мостике МД, что в данном случае устанавливается с помощью вибрационного гальванометра ВГ.
Вибрационный гальванометр отличается малой инерцией подвижной части, благодаря чему она успевает «следить» за изменением переменного тока (в противоположность баллистическому гальванометру). Причем его указатель (световой) описывает по шкале полосу.
Ширина полосы зависит от величины переменного тока, проходящего через гальванометр. С уменьшением величины тока полоса становится уже и при исчезновении тока превращается в неподвижную черточку.
Источником переменного тока в работе является трансформатор на 6 В. Требуется измерить емкость двух конденсаторов СА и СВ и батареи конденсаторов при их параллельном и последовательном соединениях и проверить формулу:
Спарал = СА + СВ,
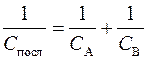 .
.
Порядок выполнения работы
1. Собрать схему с одним из конденсаторов по схеме (рис. 9).
2. Включить трансформатор и вибрационный гальванометр в осветительную сеть, установив движок Д посередине реохорда.
3. Подбором емкости в магазине емкостей добиться минимального размаха колебаний светового указателя вибрационного гальванометра.
4. Перемещением движка Д реохорда добиться полного исчезновения тока в мостике.
5. Записать подобранную магазином емкость С1 и положение движка Д в табл. 1. Вычислить по формуле (3) емкость С2 конденсатора и внести результат расчета в таблицу.
Таблица 1
| Номер опыта | Конденсатор | С1, мкФ | l1, см | l2, см | C2, мкФ | Cср, мкФ |
| I конденсатор (4 мкФ) | ||||||
| II конденсатор (6 мкФ) | ||||||
| Параллельное соединение конденсаторов I и II | ||||||
| Последовательное соединение конденсаторов I и II | ||||||
6. Проделать то же со вторым конденсатором.
7. Соединить оба конденсатора параллельно и измерить этим же способом их общую емкость Спарал.
8. Соединить оба конденсатора последовательно и измерить их общую емкость Спосл.
9. Произвести расчеты Спарал и Спосл по формулам параллельного и последовательного соединения конденсаторов, используя измеренные значения СА и СВ и сравнить их с полученными на опыте Спарал и Спосл.
10. Вычислить ошибки. Подтвердить справедливость формул параллельного и последовательного соединения конденсаторов в пределах ошибки эксперимента.
Контрольные вопросы и задания
1. Как производить измерения емкости методом мостика? Выведите рабочую формулу определения емкости этим методом.
2. Почему измерения с помощью мостика являются более точными, если искомая емкость и емкость магазина близки друг к другу?
3. Докажите, что при отсутствии тока в ветви МД потенциалы в точках М и Д совпадают по фазе.
4. Что называется емкостью уединенного проводника, конденсатора? В каких единицах измеряется, от чего зависит?
5. Выведите формулу емкости плоского конденсатора.
6. Выведите формулу емкости цилиндрического конденсатора.
7. Получите формулу емкости батареи последовательно соединенных конденсаторов.
8. Получите формулу емкости батареи параллельно соединенных конденсаторов.
9. Как определяется энергия заряженного конденсатора?
10. Определите работу, производимую при раздвижении пластин конденсатора:
a) при подключенном источнике напряжения;
б) при отключенном источнике напряжения.
11. Вычислите изменение энергии плоского конденсатора при удалении диэлектрика:
a) при подключенном источнике напряжения;
б) при отключенном источнике напряжения.
12. Как объяснить прохождение переменного электрического тока через конденсатор? Приведите пример опыта, подтверждающего это явление.
Лабораторная работа 3(4)
ИЗУЧЕНИЕ ЗАКОНА ОМА
Цель работы:проверить законы Ома для однородного и неоднородного участков цепи.
Теоретическая часть
Электрическое поле проявляет себя в действии на электрические заряды посредством кулоновской силы F® = q× Е®.. Если заряды обладают свободой передвижения, то электрическое поле приведет их в состояние упорядоченного движения – вдоль или против линий напряженности, в зависимости от знака зарядов. Такое упорядоченное движение электрических зарядов называется электрическим током, а вещества, в которых существуют свободные заряды, именуются проводниками электрического тока. В частности, к ним относятся металлы.
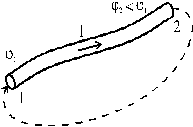 Рис. 10 Рис. 10 |
Возьмем кусок металлического провода и зарядим его концы (рис. 10), т.е. создадим между ними разность потенциалов Dj = j1 – j2. В проводнике возникает ток силой I. Если поддерживать Dj неизменной, то в этом случае, как показало исследование Г. Ома в 1921 г., сила тока пропорциональна разности потенциалов между концами проводника:
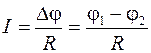 , (4)
, (4)
где R – сопротивление провода. Подчеркнем, что ток течет в сторону убывания потенциала, чем и обусловлен порядок вычитания потенциалов в формуле (4). Она носит название закона Ома для однородного участка цепи. Однородный участок – содержащий проводники только одного рода, например только металлы или только электролиты.
Каким же образом в проводнике можно поддерживать постоянный ток? Ведь перетекание зарядов от конца 1 к концу 2 вызовет уменьшение разности потенциалов концов и падение тока! Следовательно, необходимо каким-то образом непрерывно переносить приходящие к концу 2 заряды обратно на конец 1. Очевидно, эти силы должны быть не электростатического (не кулоновского) происхождения, ибо последние только противодействуют переносу зарядов в область большего потенциала. Такие не электростатические силы называют сторонними. Они действуют в источниках тока благодаря химическим, тепловым, механическим процессам, протекающим в них: гальванические элементы, аккумуляторы, термопары и термобатареи, солнечные батареи, динамо-машины.
Таким образом, для осуществления постоянного тока в проводнике необходима замкнутая цепь, в которой действует источник постоянного тока (рис. 11А). Сторонние силы характеризуют электродвижущей силой (ЭДС), которая равна работе сторонних сил по перемещению единичного заряда внутри источника.
 Рис. 11 Рис. 11 |
Участок цепи, включающий источник тока и резистор, называют неоднородным (рис. 11Б). Очевидно, для него соотношение (4) будет несправедливо, ибо кроме кулоновских на участке действуют и сторонние силы. За подробностями отсылаем читателя к учебной литературе, здесь же приведем окончательный результат:
± I× (R + r) = j1 – j2 ± e, (5)
где e – величина ЭДС, r – внутреннее сопротивление источника.
Величина U12= I × (R + r) называется напряжением на участке 12. Как видно из (5), напряжение является суммарной работой по переносу единичного заряда электростатических и сторонних сил на данном участке. Если участок однородный, т.е. e = 0, то U12 = j1 – j2, что означает совпадение значений напряжения и разности потенциалов только в случае однородного участка. Для неоднородного участка эти величины разнятся и по смыслу, и по величине.
Если точки 1 и 2 совпадают, т.е. участок превращается в замкнутую цепь, тогда j1 = j2 и (5) перепишется:
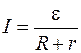 . (6)
. (6)
Эту формулу называют законом Ома для замкнутой (полной) цепи.
При использовании формулы (5) следует соблюдать правило знаков для входящих в нее величин.
1. Выбирается направление тока на участке, причем совершенно произвольно.
2. Потенциал j1 приписывается началу участка, потенциал j2 – его концу (по ходу тока).
3. ЭДС считается положительной, если направление возбуждаемого ею тока совпадает с выбранным направлением тока на участке, т.е. если по ходу тока источник находится от «–» к «+».
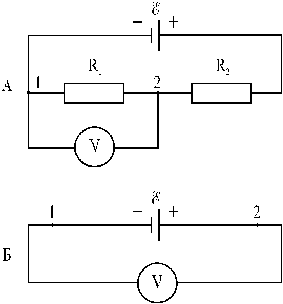 Рис. 12 Рис. 12 |
Далее возникает вопрос, как измерить Dj, U и e. Прежде всего отметим, что вольтметры большинства систем используют магнитное действие тока, для чего в самом приборе ток пропускается по катушке. Другими словами, вольтметр представляет собой однородный участок цепи. Тогда ток через него подчиняется закону (4). С другой стороны, показания прибора пропорциональны протекающему через него току. Следовательно, вольтметр измеряет разность потенциалов точек, к которым он подключен. На схеме (рис. 12А) вольтметр покажет разность потенциалов на резисторе R1, которая, согласно ранее сказанному, совпадает с напряжением на нем.
Для схемы (рис. 12Б) справедлив закон (6):
I × RV + I × r = e.
Сопротивление вольтметра велико – тысячи или десятки тысяч Ом, а сопротивление источника – единицы Ом. Поэтому I× r << I× RV, и его можно отбросить. Остается I × RV = e. Но, согласно ранее сказанному о вольтметре, I × RV = çj1 – j2ç.
Таким образом, ЭДС источника тока можно измерить, подключив высокоомный вольтметр к его полюсам.
В работе используются приборы магнитоэлектрической системы, поскольку у них направление поворота подвижной части прибора и связанной с ней стрелки зависит от направления прохождения тока через прибор. Поэтому у таких приборов возле клемм ставятся символы «+» и «-». Это означает, что плюсовая клемма должна быть подключена к точке с более высоким потенциалом, тогда отклонение стрелки будет происходить в правую (нормальную) сторону. Другими словами, внутри прибора ток протекает от клеммы «+» к клемме «-». Это позволяет по показаниям амперметра определять направление тока на участке цепи, а по показаниям вольтметра – потенциал которой точки (А или Б) выше (рис. 13). Если у прибора стрелка отклоняется в левую сторону, следует поменять местами подводящие к клеммам ток провода.
Пример. На схемах (рис. 13) показаны положения плюсовых и минусовых клемм вольтметра и амперметра. При указанной полярности включения источника стрелка амперметра будет отклоняться в правую сторону, что означает, что ток в контуре течет по часовой стрелке. У вольтметра же стрелка будет отклоняться влево, у него надо «поменять» клеммы, как показано на рис. 13Б. После этого можно будет убедиться, что потенциал точки 2 выше, чем точки 1.

Рис. 13
Порядок выполнения работы
Задание 1. Проверка закона Ома для однородного участка цепи.
Оборудование: источник тока (гальванический элемент или аккумулятор), амперметр и вольтметр магнитоэлектрической системы, три магазина сопротивлений, ключ, соединительные провода.
1. Собрать схему (рис. 14).
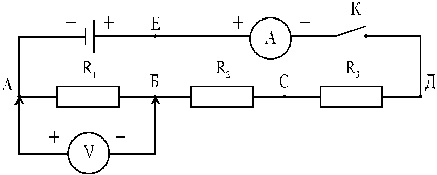 Рис. 14 Рис. 14 |
2. В качестве резисторов R1, R2, R3 использовать магазины сопротивлений. Значения сопротивлений взять кратными наименьшему сопротивлению R1, например, R1 = 100 Ом, R2 = 200 Ом, R3 = 300 Ом.
3. Измерить разность потенциалов на участках АВ, АС, АД, АЕ.
Подводящие провода к вольтметру взять со штекерами (щупами) на концах (на рис. 14 показаны со стрелками), чтобы можно было оперативно менять полярность его включения и подключать к разным точкам цепи.
4. Результаты измерений занести в табл. 2.
Таблица 2
| I | Dj, В | |||||
| Цена деления, мА/дел. | Показания в делениях | Показания в мА | АВ | АС | АД | АЕ |
5. По полученным данным вычислить разности потенциалов DjВС и DjСД.
6. По формуле (4) найти теоретические значения R1, R2, R3 и сравнить их с экспериментальными, т.е. со значениями сопротивлений, установленными на магазинах. Результаты сравнения привести в конце отчета и сделать вывод.
7. Проверить соотношения 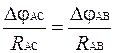 или
или 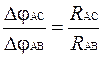 , используя экспериментальные значения Dj и R (Так как в цепи нет разветвлений, ток на всех участках одинаков, то из (4) следует, что отношение
, используя экспериментальные значения Dj и R (Так как в цепи нет разветвлений, ток на всех участках одинаков, то из (4) следует, что отношение 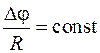 – для всех участков). Результаты вычислений занести в табл. 3.
– для всех участков). Результаты вычислений занести в табл. 3.
8. Результаты проверки внести в выводы работы.
Таблица 3
| RАВ, Ом | RВС, Ом | RСД, Ом | DjАС/ DjАВ | RАС/RАВ | DjАД/DjАВ | RАД/RАВ | DjАД/DjАС | RАД/RАС | |||
| теор. | эксп. | теор. | эксп. | теор. | эксп. | ||||||
Задание 2. Проверка закона Ома для неоднородного участка цепи.
Оборудование: остается тем же, что и в задании 1, лишь добавляется двойной ключ П и еще один источник тока.
1. Собрать схему (рис. 15), которая является модификацией схемы на рис. 14. Двойной ключ П служит для изменения направления действия источника e1.
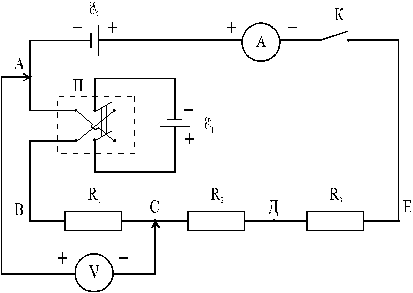
Рис. 15
2. Измерить ток в цепи в одном из положений двойного ключа (одна полярность включения e1 в цепь).
3. Измерить разность потенциалов на участках АВ, АС, АД, АЕ.
4. Измерить величину ЭДС e1 и определить ее знак в данном положении ключа.
Примечание. Знак и величина e1 измеряются путем подключения вольтметра к точкам А и В при разомкнутом ключе К. Например, если стрелка вольтметра отклоняется вправо при подключении «+» клеммы к точке А ( положительное показание цифрового вольтметра), e1 создает ток, текущий от точки В к точке А, и в соответствии с правилом знаков эта ЭДС отрицательна.
5. Изменить положение двойного ключа (другая полярность включения e1 в цепь).
6. Повторить измерения силы тока и разностей потенциалов на тех же участках.
7. Измерить величину ЭДС e1 и определить ее знак в измененном положении ключа.
8. Занести результаты измерений с учетом знаков в табл. 4.
Таблица 4
| Номер опыта | I | Dj | e, В | |||||
| Цена деления, мА/дел. | Показания амперметра | Показания вольтметра на участках, В | ||||||
| в делениях | в мА | АВ | АС | АД | АЕ | |||
| 1. | ||||||||
| 2. |
9. Используя результаты измерений разности потенциалов, ЭДС и значения сопротивлений на участках, рассчитать по формуле 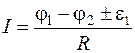 (полученной из формулы (5)) силу тока в цепи для обоих вариантов включения e1 в цепь. Причем в формулу все величины следует подставлять с учетом их знаков.
(полученной из формулы (5)) силу тока в цепи для обоих вариантов включения e1 в цепь. Причем в формулу все величины следует подставлять с учетом их знаков.
10. Результаты расчета и эксперимента занести в табл. 5. За экспериментальное значение силы тока будем принимать то значение, что показывает амперметр, а за теоретическое будем принимать значение силы тока, рассчитанное по формуле.
11. Результаты сравнения привести в конце отчета и сделать вывод.
Таблица 5
| Номер опыта | e1, В | Iэксп, мА | I теор, мА | Iтеор ср, мА | ||
| АС | АД | АЕ | ||||
Контрольные вопросы и задания
1. Каковы условия существования постоянного тока?
2. Запишите и поясните закон Ома для однородного участка цепи.
3. Запишите закон Ома для неоднородного участка цепи. Поясните правило знаков.
4. Что измеряет вольтметр?
5. Как определить величину ЭДС, ее знак?
6. Как определить внутреннее сопротивление источника тока? Найдите внутреннее сопротивление r1 по результатам задания 2.
7. По результатам задания 1 найдите сопротивление амперметра.
Лабораторная работа 4(6)
