Законы теплового излучения
3.1.Максимум спектральной плотности энергетической светимости Солнца приходится на длину волны 0,48 мкм. Считая, что Солнце излучает как чёрное тело, определить температуру его поверхности и мощность, излучаемую его поверхностью. [6,04 кК; 4,58·1026 Вт].
3.2.Определить количество теплоты, теряемой 50 см2 поверхности расплавленной платины за 1 мин, если поглощательная способность платины 0,8. Температура плавления платины равна 1770оС. [237 кДж].
3.3.Определить, во сколько раз необходимо уменьшить температуру чёрного тела, чтобы его энергетическая светимость ослабилась в 16 раз. [В 2 раза].
3.4.Энергетическая светимость чёрного тела равна 10 кВт/м2. Определить длину волны, соответствующую максимуму спектральной плотности энергетической светимости этого тела. [4,47 мкм].
3.5. Определить, как и во сколько раз изменится мощность излучения чёрного тела, если длина волны, соответствующая максимуму его спектральной плотности энергетической светимости, сместилась с 720 нм до 400 нм. [Увеличится в 10,5 раз].
3.6.Чёрное тело находится при температуре 3000 К. При остывании тела длина волны, соответствующая максимуму энергетической светимости, изменилась на 8 мкм. Определить температуру, до которой тело охладилось. [323 К].
3.7.Чёрное тело нагрели от температуры 600 К до 2400 К. Определить: 1) во сколько раз увеличилась его энергетическая светимость; 2) на сколько уменьшилась длина волны, соответствующая максимуму спектральной плотности энергетической светимости. [1) в 256 раз; 2) на 3,62 мкм].
3.8.В результате нагревания чёрного тела длина волны, соответствующая максимуму спектральной плотности энергетической светимости, сместилась с 2,7 мкм до 0,9 мкм. Определить, во сколько раз увеличилась: 1) энергетическая светимость тела; 2) максимальная спектральная плотность энергетической светимости тела. [1) в 81 раз; 2) в 243 раза].
3.9.Считая никель чёрным телом, определить мощность, необходимую для поддержания температуры расплавленного никеля 1453 ºС неизменной, если площадь его поверхности равна 0,5 см2. Потерями энергии пренебречь. [25,2 Вт].
3.10. Металлическая поверхность площадью 15 см2, нагретая до температуры 3000 К, излучает в одну минуту 100 кДж. Определить: 1) энергию, излучаемую этой поверхностью, считая её чёрной; 2) отношение энергетических светимостей этой поверхности и чёрного тела при данной температуре. [1) 413 кДж; 2) 0,242].
3.11.Принимая Солнце за чёрное тело и учитывая, что его максимальной спектральной плотности энергетической светимости соответствует длина волны 500 нм, определить: 1) температуру поверхности Солнца; 2) энергию, излучаемую Солнцем в виде электромагнитных волн за 10 мин; 3) массу, теряемую Солнцем за это время вследствие излучения. [1) 5,8 кК; 2) 2,34·1029Дж; 3) 2,6·1012 кг].
3.12.Мощность излучения чёрного тела равна 34 кВт. Найти температуру этого тела, если его поверхность равна 0,6 м2. [1000 К].
3.13.Температура вольфрамовой спирали в 25-ваттной электрической лампочке равна 2450 К. Отношение энергетической светимости лампочки и черного тела при данной температуре равно 0,3. Найти величину излучающей поверхности спирали. [4·10-5м2].
3.14.Мощность излучения чёрного тела равна 105 кВт. Найти величину излучающей поверхности тела, если известно, что длина волны, на которую приходится максимум спектральной плотности энергетической светимости, равна 700 нм. [14,4 см2].
3.15.Найти, какое количество энергии с одного квадратного сантиметра поверхности в одну секунду излучает чёрное тело, если известно, что максимум спектральной плотности энергетической светимости приходится на длину волны 4840 Å. [7350 Дж].
3.16.В каких областях спектра лежат длины волн, соответствующие максимуму спектральной плотности энергетической светимости, если в качестве источника света взять: 1) спираль электрической лампочки (Т=3000 К); 2) поверхность Солнца (Т=6000 К); 3) атомная бомба, имеющая в момент взрыва около 10 млн. градусов. Излучение считать близким к излучению чёрного тела. [1) 1 мкм; 2) 500 нм; 3) 2,9 Å].
3.17.На сколько процентов увеличится энергетическая светимость чёрного тела, если его температура увеличится на 1%? [На 4%].
Внешний фотоэффект
3.18.Красная граница фотоэффекта для цезия 6530 Å. Определить скорость фотоэлектронов при облучении цезия светом длиной волны 4000 Å. [6,5·105 м/с].
3.19.Определить работу выхода электронов из натрия, если «красная граница» фотоэффекта равна 5000 Å. [2,49 эВ].
3.20.Определить максимальную скорость фотоэлектронов, вырываемых с поверхности металла, если фототок прекращается при задерживающем напряжении 3,7 В. [1,14 Мм/с].
3.21.«Красная граница» фотоэффекта для некоторого металла равна 500 нм. Определить минимальное значение энергии фотона, вызывающего фотоэффект. [2,49 эВ].
3.22. Калий освещается монохроматическим светом с длиной волны 400 нм. Определить наименьшее задерживающее напряжение, при котором фототок прекратится. Работа выхода электронов из калия равна 2,2 эВ. [0,91 В].
3.23.«Красная граница» фотоэффекта для некоторого металла равна 500 нм. Определить: 1) работу выхода электронов из этого металла; 2) максимальную скорость электронов, вырываемых из этого металла светом с длиной волны 400 нм. [1) 2,49 эВ; 2) 468 км/с ].
3.24.Длина волны падающего света 400 нм, задерживающее напряжение равно 1,2 В. Определить «красную границу» фотоэффекта. [652 нм].
3.25. Задерживающее напряжение для платиновой пластины (работа выхода 6,3 эВ) составляет 3,7 В. При тех же условиях для другой пластины задерживающее напряжение равно 5,3 В. Определить работу выхода электронов из этой пластины. [4,7 эВ].
3.26.Фотоны с энергией 5 эВ вырывают фотоэлектроны из металла с работой выхода 4,7 эВ. Определить максимальный импульс, передаваемый поверхности этого металла при вылете электрона. [2,96·10-25 кг·м/с].
3.27.Определить максимальную скорость фотоэлектронов, вырываемых с поверхности цинка (работа выхода 4 эВ), при облучении светом длиной волны 2,47 пм. [259 Мм/с].
3.28.Фотоэффект для некоторого металла начинается при частоте падающего света 6·1014 Гц. Задерживающее напряжение равно 3 В. Определить: 1) работу выхода электронов из этого металла; 2) частоту применяемого излучения. [1) 2,48 эВ; 2) 1,32·1015 Гц].
3.29.Определить постоянную Планка, если известно, что фотоэлектроны, вырываемые с поверхности некоторого металла светом с частотой 2,2·1015 Гц, полностью задерживаются напряжением 6,6 В, а вырываемые светом с частотой 4,6·1015 Гц – напряжением 16,5 В. [6,6·10-34 Дж·с].
3.30.При освещении катода вакуумного фотоэлемента светом с длиной волны 310 нм фототок прекращается при некотором задерживающем напряжении. При увеличении длины волны на 25% задерживающее напряжение оказывается меньше на 0,8 В. Определить по этим данным постоянную Планка. [6,61·10-34 Дж·с].
Давление света
3.31.Давление света с длиной волны 500 нм на зачернённую поверхность, расположенную перпендикулярно падающим лучам, равно 0,12 мкПа. Определить число фотонов, падающих ежесекундно на 1 м2 поверхности. [9,05·1019].
3.32.На идеально отражающую поверхность площадью 5 см2 за время 3 мин нормально падает монохроматический свет, энергия которого 9 Дж. Определить световое давление, оказываемое на поверхность. [667 нПа].
3.33.Определить давление света на стенки электрической 150-ваттной лампочки, принимая, что вся потребляемая мощность идёт на излучение и стенки лампочки отражают 15% падающего на них света. Считать лампочку сферическим сосудом радиусом 4 см. [28,6 мкПа].
3.34.Давление света с длиной волны 500 нм на зачернённую поверхность, расположенную перпендикулярно падающему излучению, равно 0,15 мкПа. Определить число фотонов, падающих на поверхность площадью 10 см2 за 1 с. [4,52·1017].
3.35.На поверхность площадью 100 см2 ежеминутно падает 63 Дж световой энергии. Определить величину светового давления в случаях, когда поверхность: 1) полностью отражает все лучи; 2) полностью поглощает все падающие на неё лучи. [1) 7·10-7 Па; 2) 3,5·10-7 Па].
3.36.Пучок света с длиной волны 4900 Å, падая нормально на поверхность, производит давление 5·10-6 Па. Сколько квантов света падает ежесекундно на единицу площади этой поверхности? Коэффициент отражения света равен 0,25. [2,9·1021].
3.37.На идеально отражающую плоскую поверхность нормально падает свет с длиной волны 0,55 мкм. Мощность излучения составляет 0,45 Вт. Определить: 1) число фотонов, падающих на поверхность за время 3 с; 2) силу давления, испытываемую этой поверхностью. [1) 3,73·1018; 2) 3 нН].
3.38.На зеркало с идеально отражающей поверхностью 1,5 см2 падает нормально свет от электрической дуги. Определить импульс, полученный зеркалом. Плотность потока световой энергии, падающей на него, равна 10 Вт/см2, а продолжительность освещения 1 с. [10-7 кг·м/с].
3.39.Поток излучения с длиной волны 5000 Å падает нормально на плоскую зеркальную поверхность и давит на неё с силой 10-8 Н. Определить число фотонов, ежесекундно падающих на эту поверхность. [3,78·1018].
Эффект Комптона
3.40.Рентгеновские лучи с длиной волны 0,708 Å испытывают комптоновское рассеяние на парафине. Найти длину волны рентгеновских лучей, рассеянных в направлении: 1)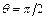 
; 2)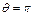 
. [1) 0,732 Å; 2) 0,756 Å].
3.41.Какова длина волны рентгеновского излучения, если при комптоновском рассеянии этого излучения графитом под углом 60º длина волны рассеянного излучения оказалась равной 2,54·10-7 м? [0,242 Å].
3.42.Рентгеновские лучи с длиной волны 0,2 Å испытывают комптоновское рассеяние под углом 90º. Определить: 1) изменение длины волны рентгеновских лучей при рассеянии; 2) энергию электрона отдачи; 3) импульс электрона отдачи. [1) 0,024 Å; 2) 6,6·103 эВ; 3) 4,4·10-23 кг·м/с].
3.43.В явлении Комптона энергия падающего фотона распределяется поровну между рассеянным фотоном и электроном отдачи. Угол рассеяния равен 90º. Определить энергию и импульс рассеянного фотона. [2,6·105 эВ; 9,3·10-12 кг·м/с].
3.44.Энергия рентгеновских лучей равна 0,6 МэВ. Определить энергию электрона отдачи, если известно, что длина волны рентгеновских лучей после комптоновского рассеяния изменилась на 20%. [0,1 МэВ].
3.45.Фотон с энергией 1,025 МэВ рассеялся на первоначально покоящемся свободном электроне. Определить угол рассеяния фотона, если длина волны рассеянного фотона оказалась равной 2,43 нм. [60º].