Квантовая теория строения атома водорода по бору. объяснение спектров излучения и поглощения водорода. квантовые числа. принцип паули. правила отбора

Спектры атомов подразделяют на спектры испусканияи спектрыпоглощения. Для получения спектра испускания водорода его необходимо разогреть до высокой температуры и излучение пропустить через оптическую систему, состоящую из коллиматора и призмы. При этом на экране, размещенном за призмой, можно наблюдать тонкие цветные линии, образующие спектральную серию, называемую серией Бальмера. Частоты спектральных линий серии Бальмера определяются из формулы:

, ,

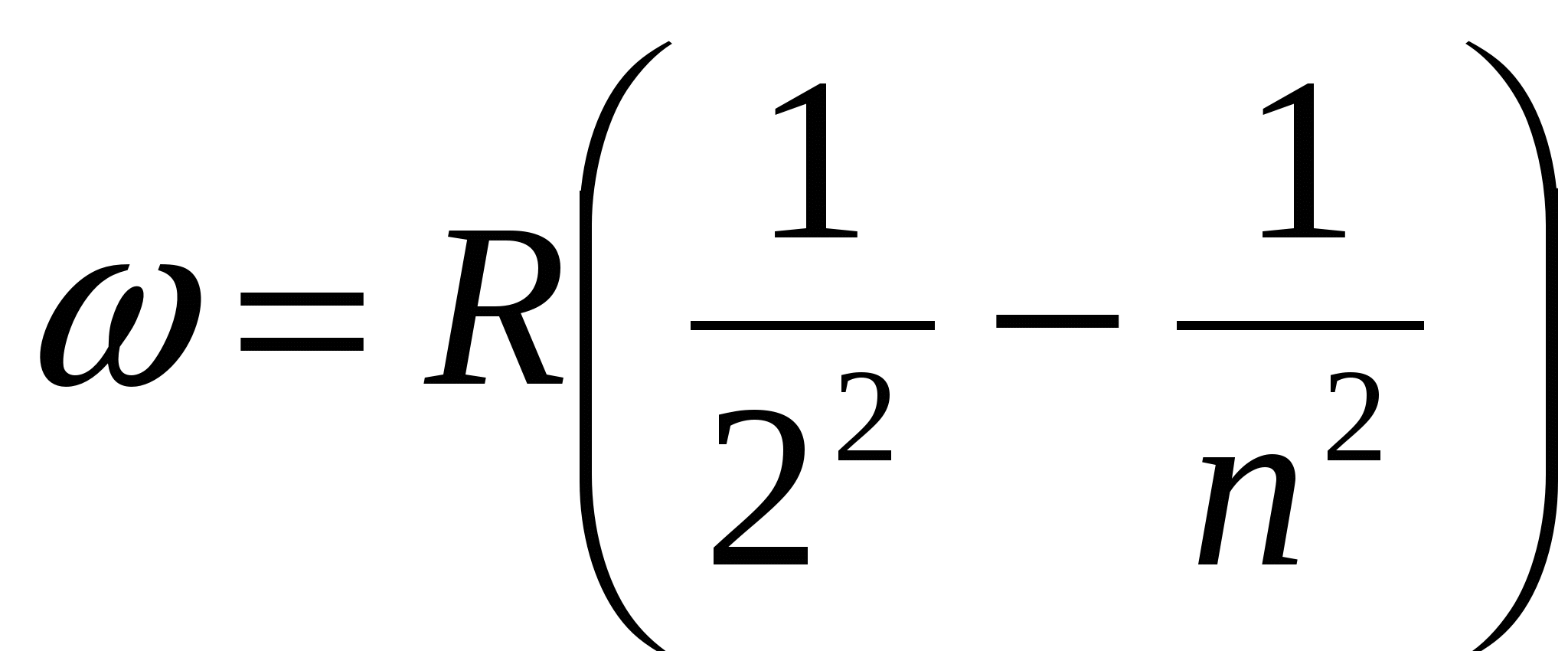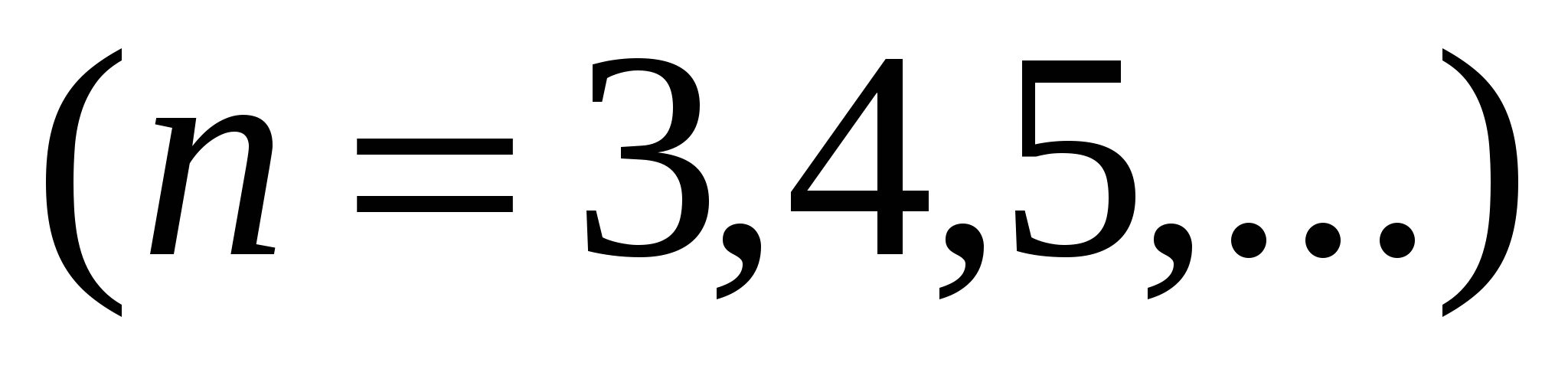где 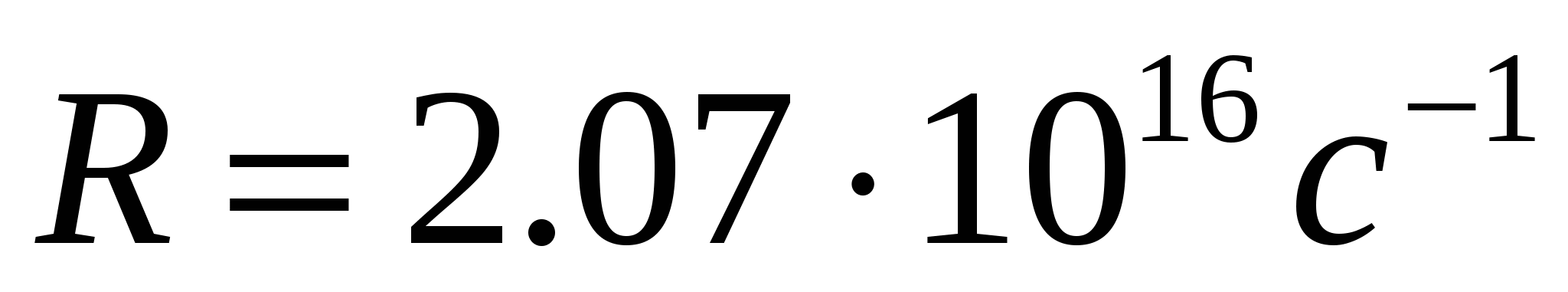- постоянная Ридберга. Кроме одной спектральной серии, расположенной в видимой части спектра, у водорода имеется одна спектральная серия в ультрафиолете, называемая серией Лаймана:

,

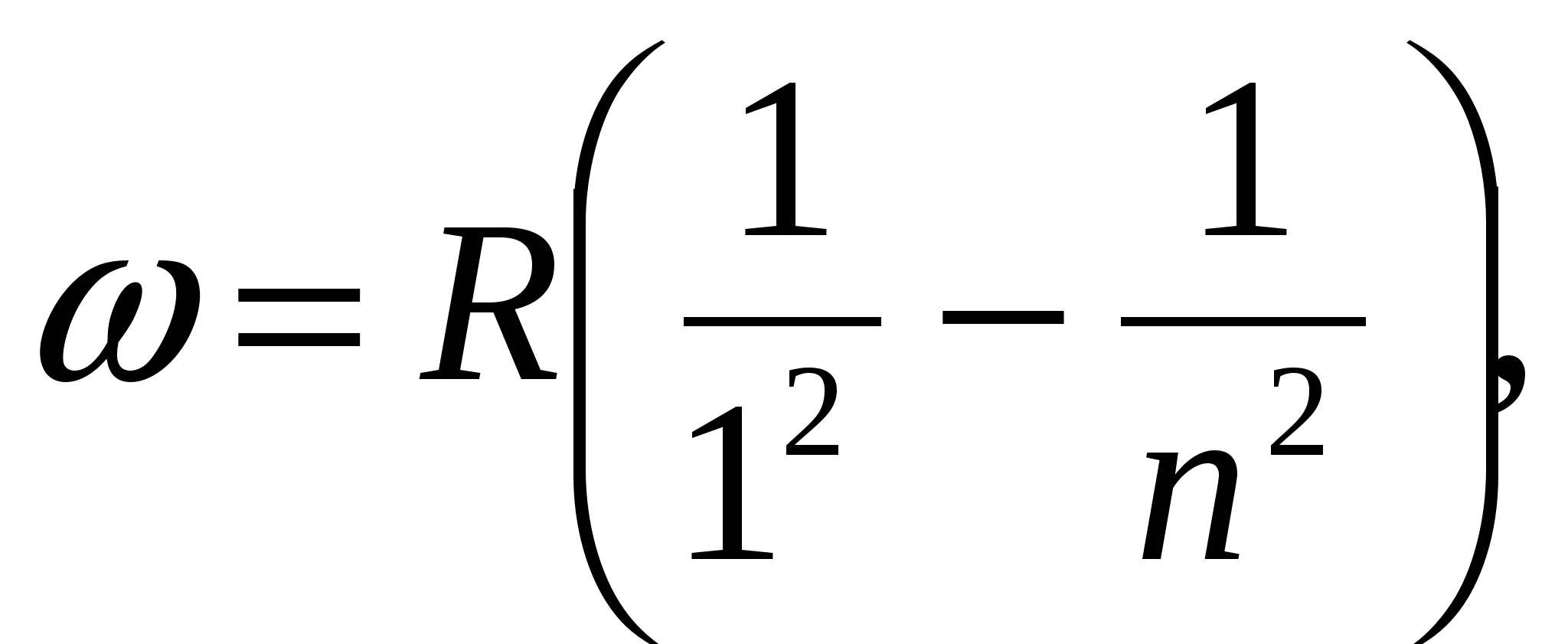
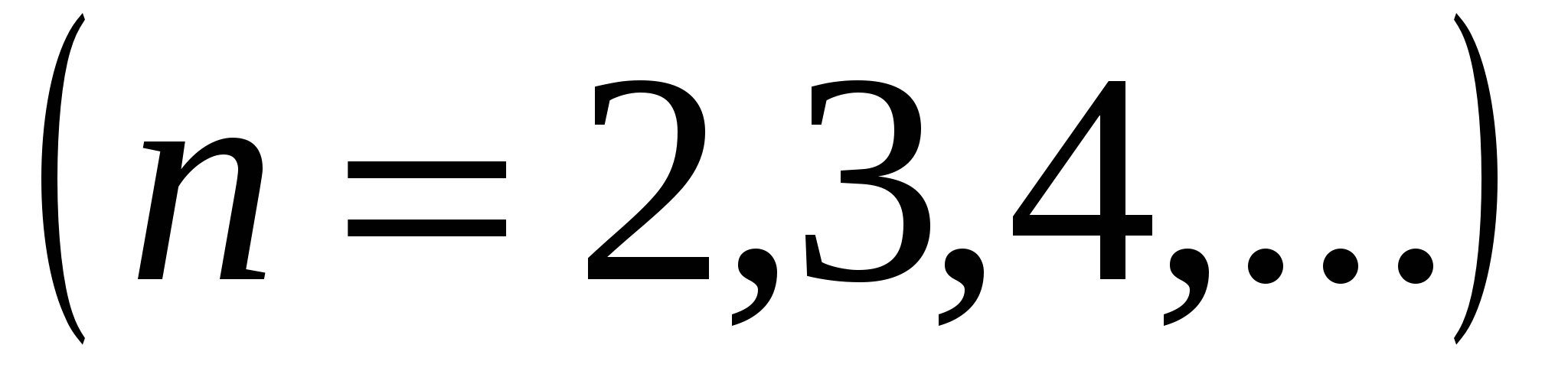а также спектральные серии в инфракрасной части спектра:

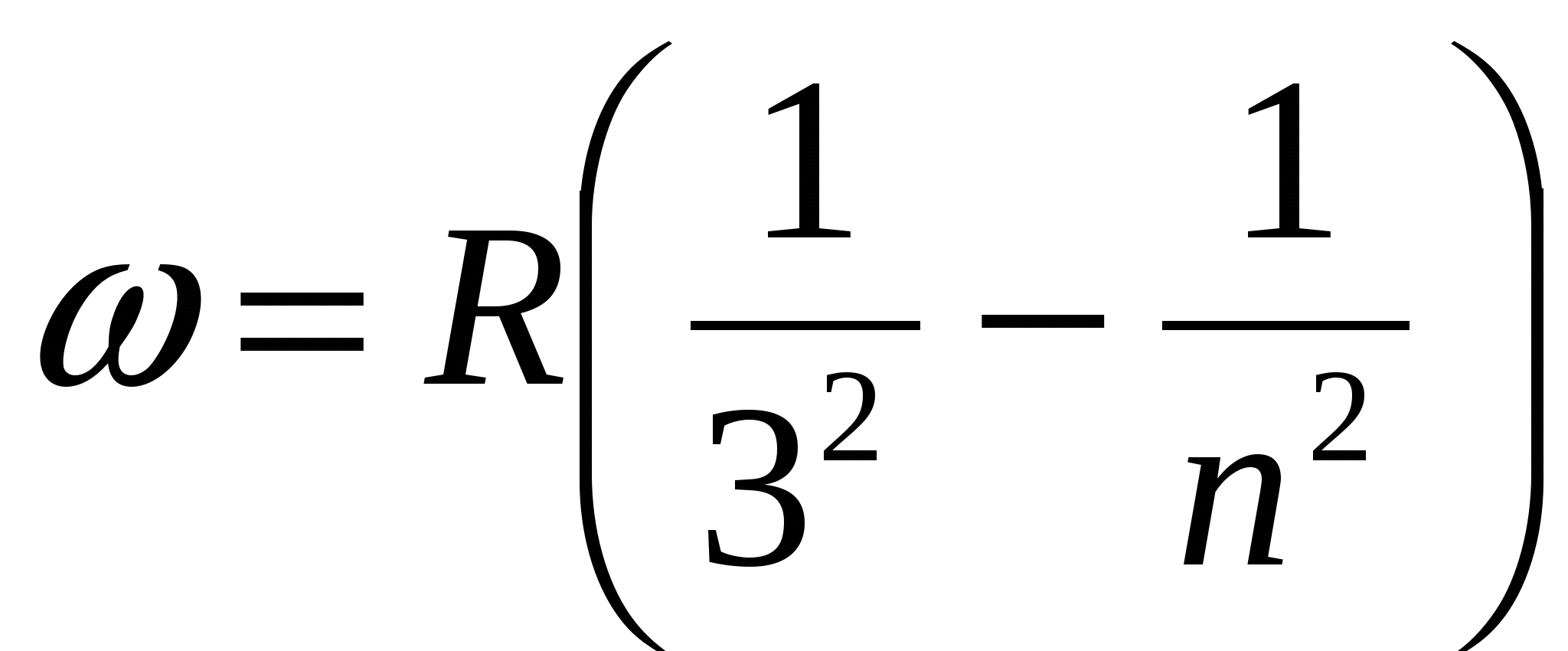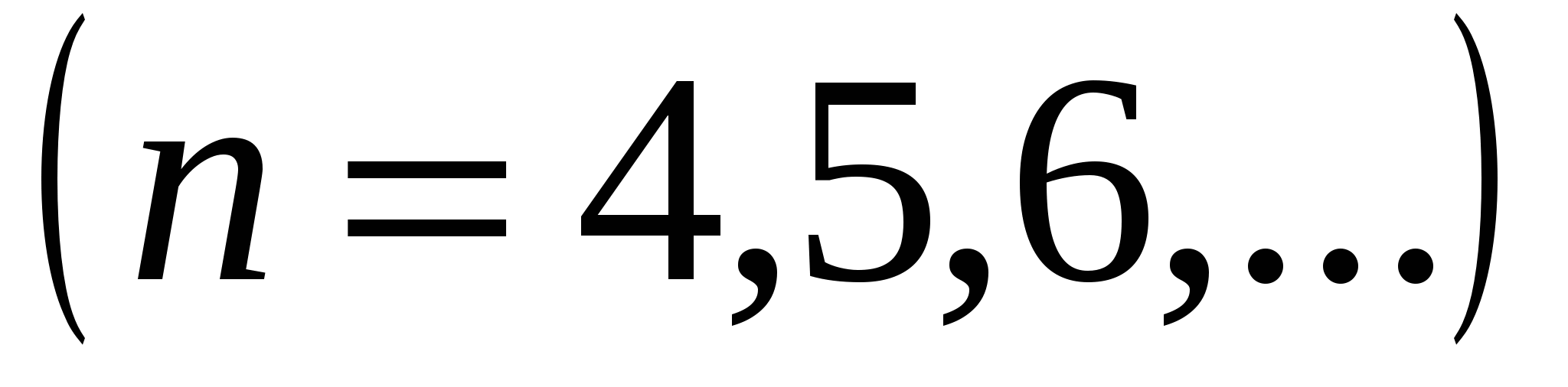, , (серия Пашена),

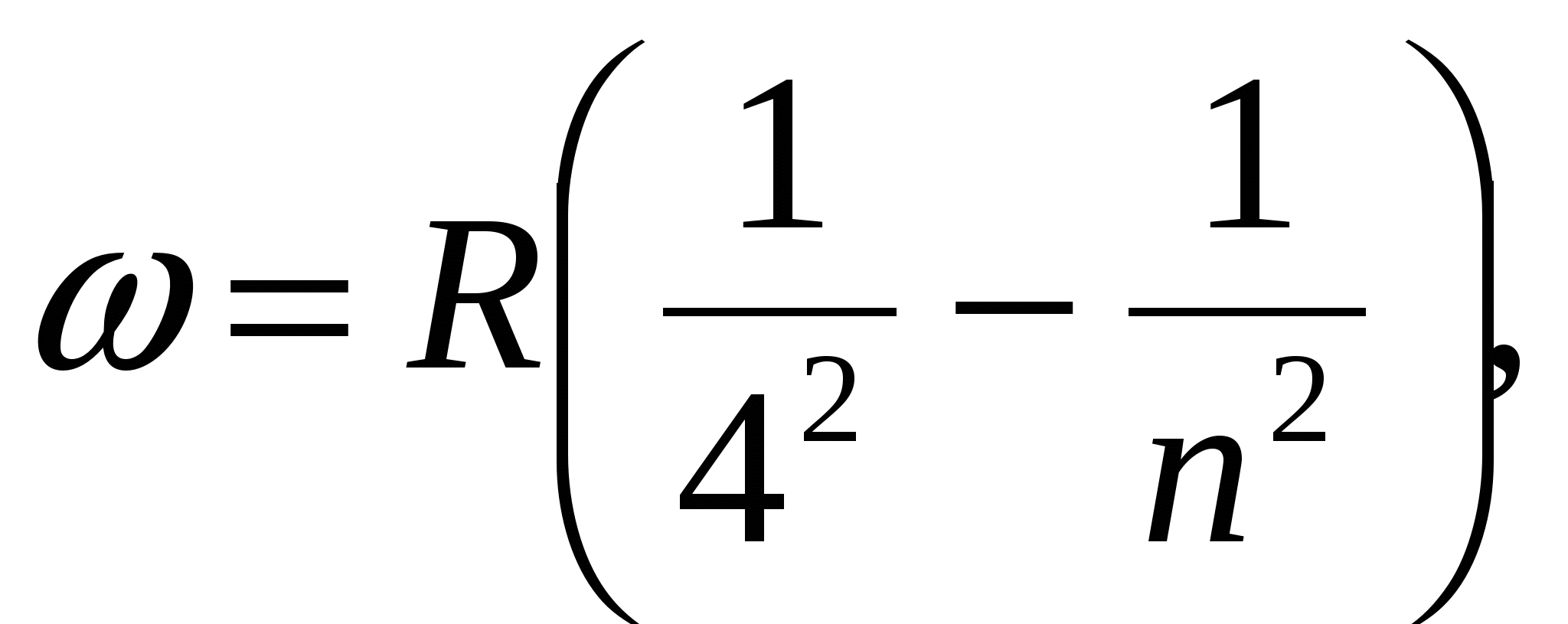
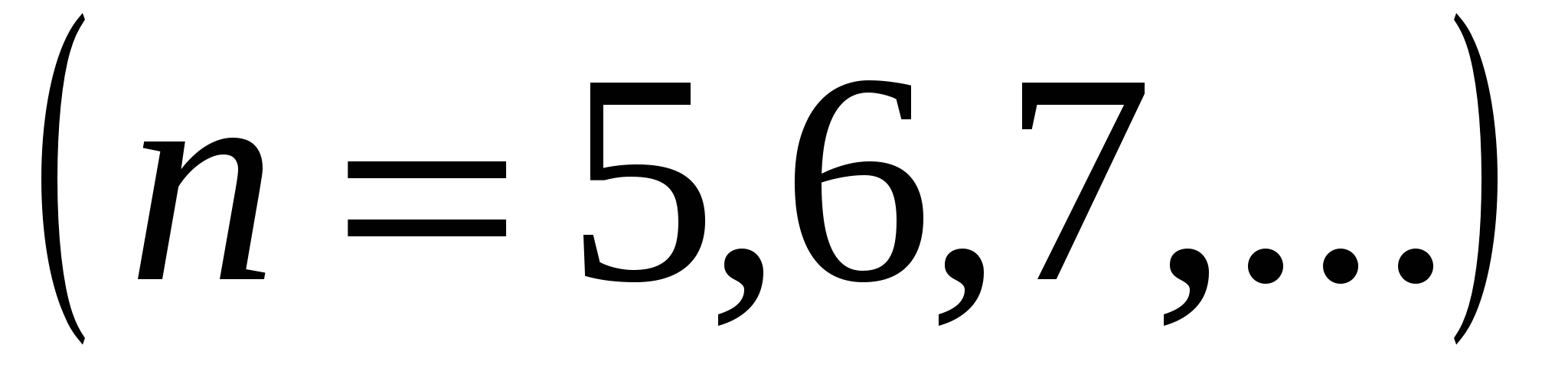, (серия Брэкета),

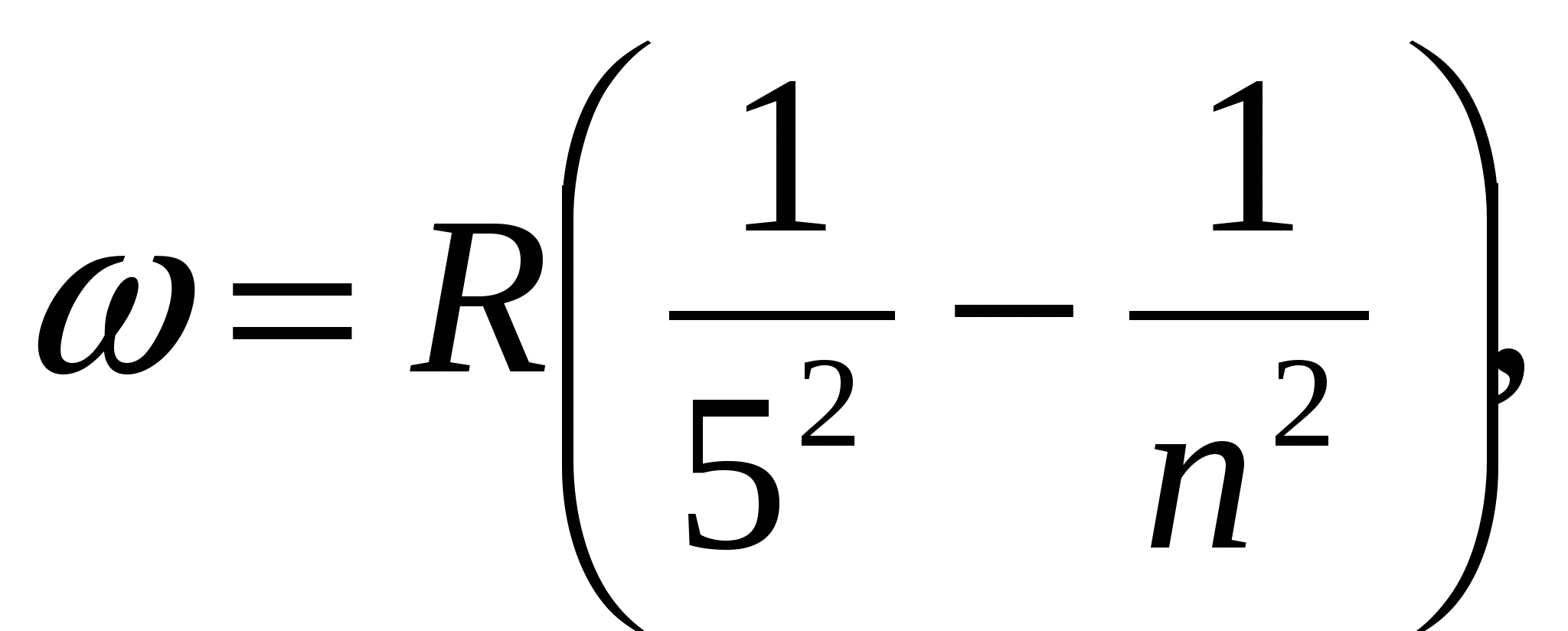
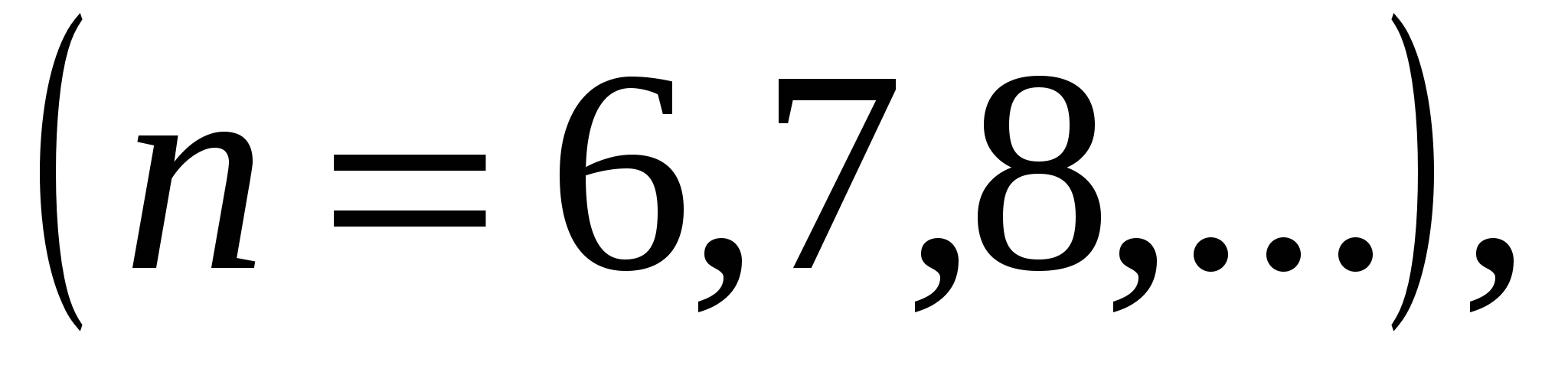(серия Пфунда).

В низкочастотной области спектр атома водорода простирается вплоть до радиодиапазона. В настоящее время в спектре межзвездного водорода обнаружены спектральные линии, соответствующие длинам волн 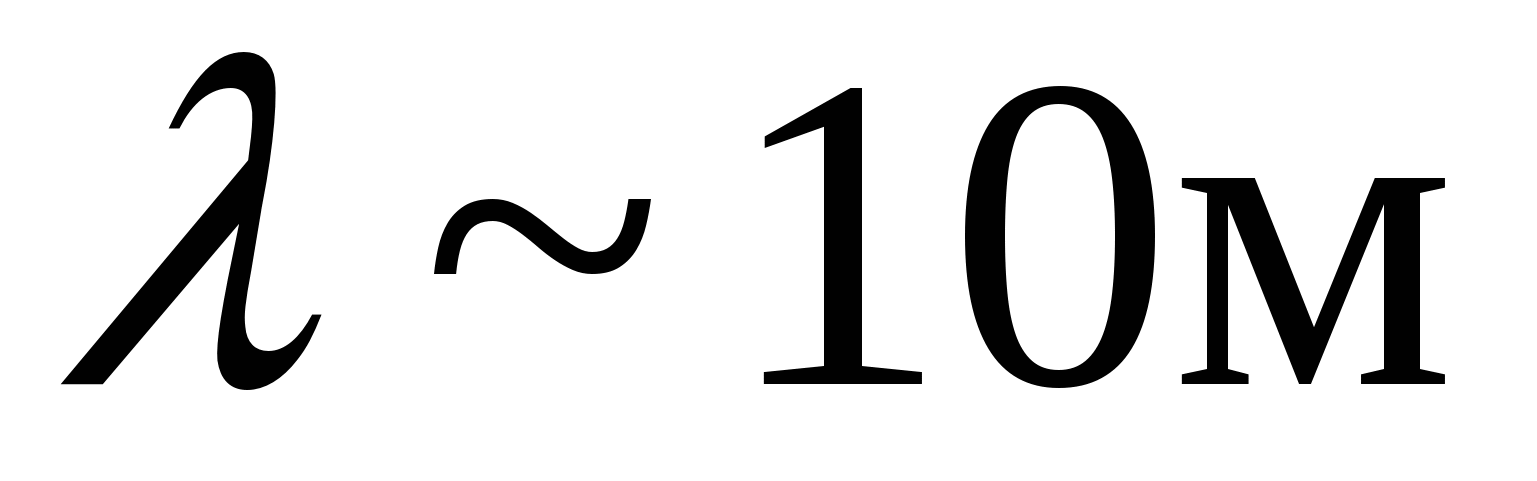. Если обратить внимание на структуру соотношений (6.1)-(6.5), то видно, что все они могут быть представлены в общем виде:

,

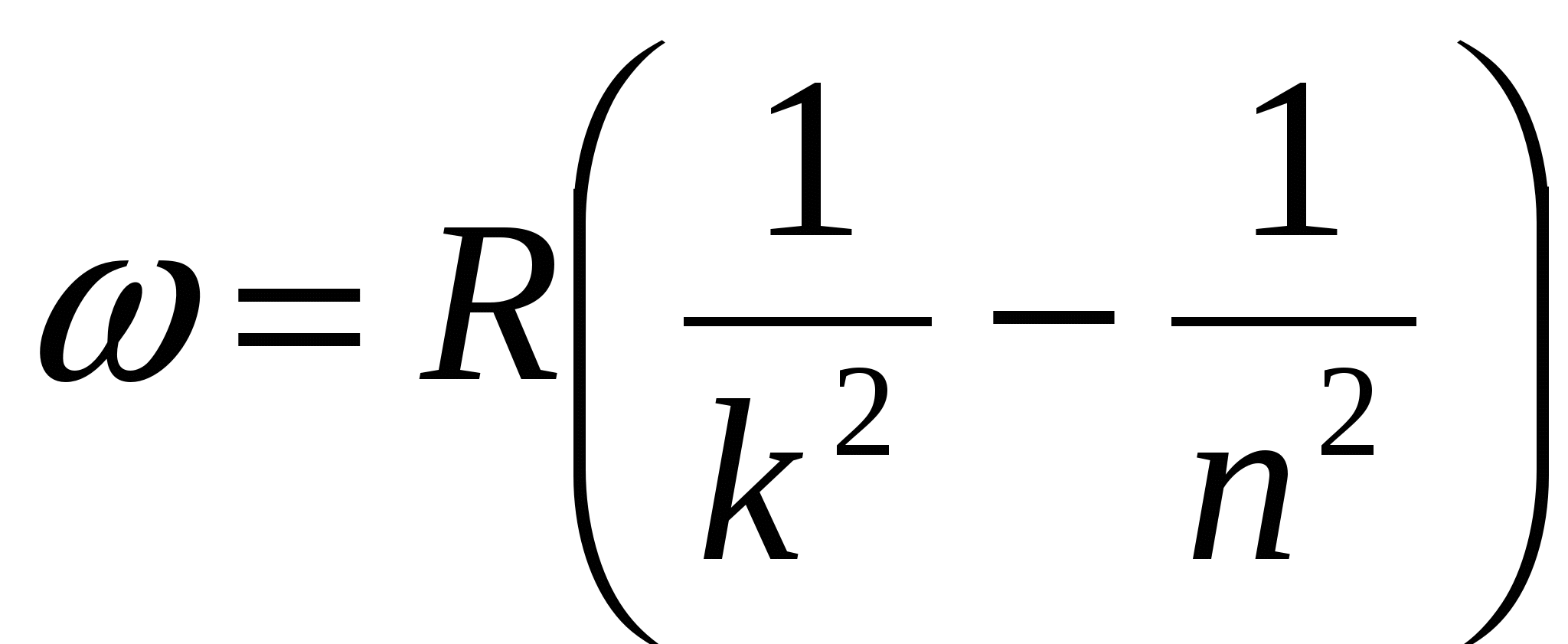где 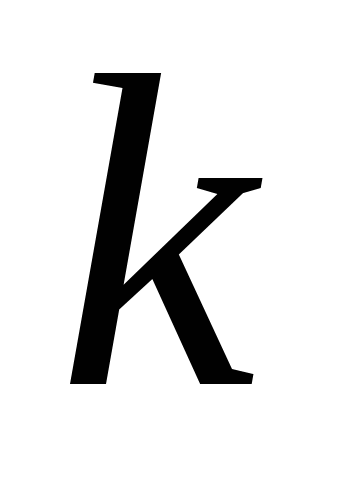и 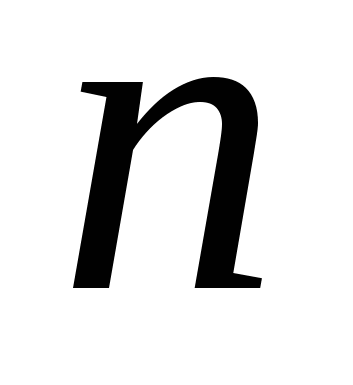целые числа, причем 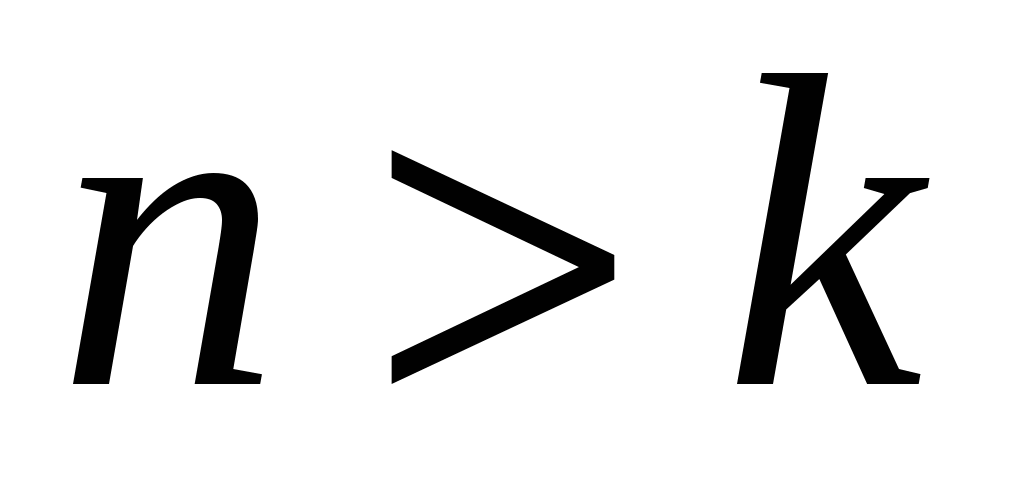. Соотношение называют обобщенной формулой Бальмера.

Спектр поглощения водорода можно получить при пропускании через него электромагнитного излучения с непрерывным спектром. Тогда после прохождения через коллиматор и призму излучение на экране разворачивается в спектр, представляющий собой радугу на фоне которой заметны тонкие черные полоски. Черным полоскам соответствуют частоты, определяемые формулой. Таким образом, спектр излучения и спектр поглощения водорода взаимно дополняют друг друга до радуги.

При́нцип Па́ули (принцип запрета) — один из фундаментальных принципов квантовой механики, согласно которому два и более тождественныхфермиона (частиц с полуцелым спином) не могут одновременно находиться в одном квантовом состоянии.

Ква́нтовое число́ в квантовой механике — численное значение какой-либо квантованной переменной микроскопического объекта (элементарной частицы, ядра, атома и т. д.), характеризующее состояние частицы. Задание квантовых чисел полностью характеризует состояние частицы.

Некоторые квантовые числа связаны с движением в пространстве и характеризуют вид волновой функции частицы. Это, например, радиальное (главное) ( 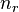), орбитальное ( 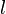),магнитное ( 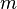) и спиновое квантовые числа электрона в атоме, которые определяются как число узлов радиальной волновой функции, значение орбитального углового момента, его проекция на заданную ось и спин частицы, соответственно.