Сигналы при дискретной модуляции

При дискретной модуляции закодированное сообщение u(t), представляющее собой последовательность кодовых символов { 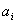}, преобразовывается в последовательность элементов сигнала { 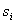}. Последние отличаются от кодовых символов лишь электрическим представлением. В частном случае дискретная модуляция состоит в воздействии кодовых символов {аi} на переносчик f(t). Такая дискретная модуляция аналогична непрерывной.

Посредством модуляции один из параметров переносчика изменяется по закону, определяемому кодом. При непосредственной передаче переносчиком может быть постоянный ток, изменяющимися параметрами которого являются величина и направление. Обычно же в качестве переносчика, как и при непрерывной модуляции, используется переменный ток (гармоническое колебание). В этом случае можно получить амплитудную (AM), частотную (ЧМ) и фазовую (ФМ) модуляции. Дискретную модуляцию часто называют манипуляцией, а устройство, осуществляющее дискретную модуляцию (дискретный модулятор), называют манипулятором или генератором сигналов.

На рис. 3.4 приведены графики сигналов при различных видах манипуляции. При AM символу 1 соответствует передача несущего колебания в течение времени 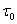(посылка), символу 0 — отсутствие колебания (пауза). При ЧМ передача несущего колебания с частотой 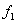соответствует символу 1, а передача колебания 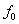соответствует 0. При ФМ меняется фаза несущей на 180° при каждом переходе от 1 к 0 и от 0 к 1.

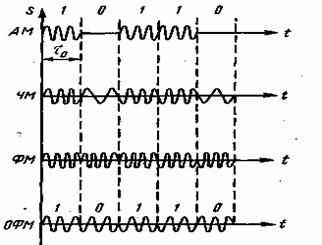
Рис. 3.4. Сигналы при различных видах дискретной модуляции

Рассмотрим спектры сигналов при некоторых видах дискретной модуляции. Будем полагать, что модуляция производится двоичным сообщением u(t), представляющим собой периодическую последовательность прямоугольных импульсов с периодом .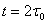

Амплитудная манипуляция. Сигнал AM можно записать в виде

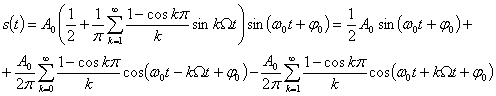(3.35)

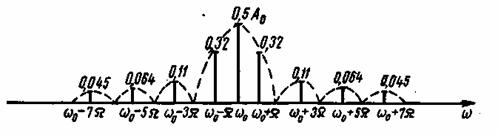
Рис. 3.5. Спектр сигнала при амплитудной манипуляции

Спектр сигнала AM, построенный по ф-лам (3.35), показан на рис. 3.5. Он состоит из несущего колебания с амплитудой 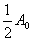и двух боковых полос, спектральные составляющие которых имеют амплитуды

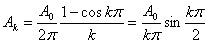(3.36)

Огибающая спектра дискретного сигнала AM выражается формулой

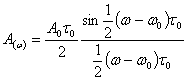(3.37)

Фазовая манипуляция. Сигнал ФМ можно записать в виде

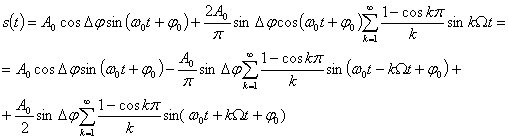(3.40)

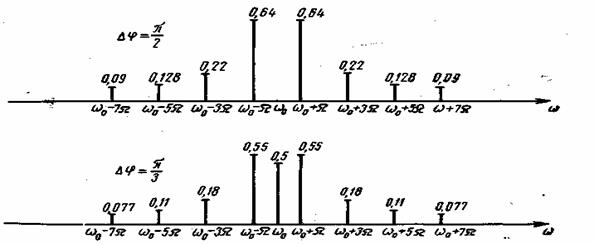
Рис. 3.6. Спектры сигналов при фазовой манипуляции

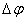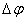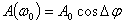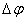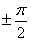Спектр сигнала ФМ для различных значений девиаций фазы , построенной на основании ф-лы (3.40), показан на рис. 3.6. Он состоит из несущего колебания и двух боковых полос. Амплитуда несущего колебания зависит от : и при = — обращается в 0. Амплитуды спектральных составляющих в боковых полосах также зависят от 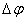. При увеличении 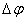от 0 до 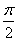, как видно из рис. 3.6, амплитуда несущего колебания убывает до нуля, а амплитуды боковых частот увеличиваются.

Когда 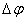= 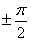— вся энергия сигнала ФМ содержится только в боковых полосах. Так же, как и при AM, огибающая дискретного спектра боковых частот представляет собой смещенный на частоту 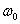спектр одиночного импульсного сигнала u(t), умноженный нa sin :

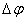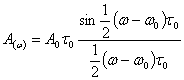(3.41)

Аналогично определяется спектр сигнала при частотной манипуляция.

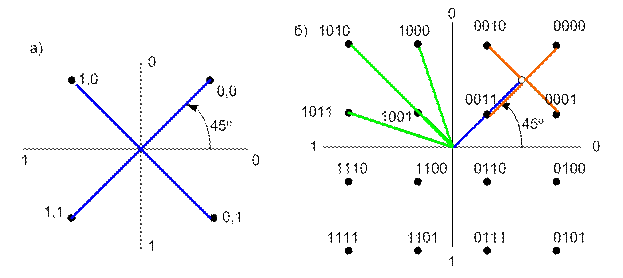
Сигнально-кодовые конструкции.Сигнально-кодовые конструкции позволяют отображать способ модуляции, при котором в общем случае изменяется и фаза и амплитуда модулируемого сигнала. Для этого исходные коды принято изображать на плоскости в виде точек, полярные координаты которых соответствуют значениям фазы и амплитуды модулируемого сигнала.При использовании такого способа кодирования каждый бодовый интервал несет на себе несколько бит. При использовании 4 точек (состояний) каждая точка описывается двумя битами, для 16 точек получаем квадрибит (четыре бита) и т.д.

23-24. Некогерентный амплитудный детектор. Принцип действия, СХД в режимах больших амплитуд и малых амплидут

Детектор огибающий.

Основные СХД: ig=ψ(Um)

ig=I₀ – i₀ где I₀ – постоянная составляющая тока, i₀-ток покоя

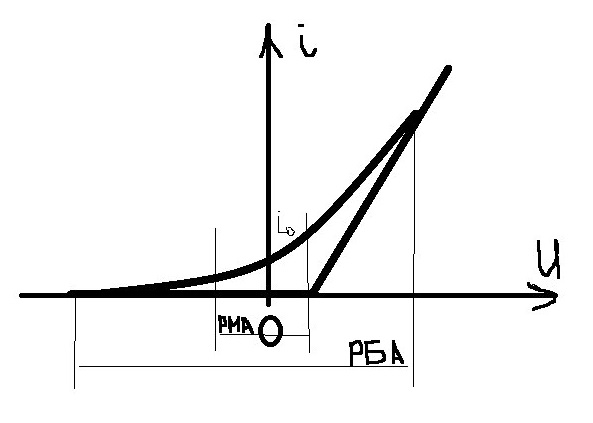
ВАХ VD

Различают два режима работы детектора:

1) Режим малых амплитуд

2) Режим больших амплитуд.

РБА. Аппроксимируем двумя отрезками прямых

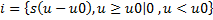
i₀=0

I=SUmϒ(ϴ)

Если ϴ=π/2 , то

I₀=SUm/π – неискаженный режим

Вывод: в РБА СХД линейная!

РМА

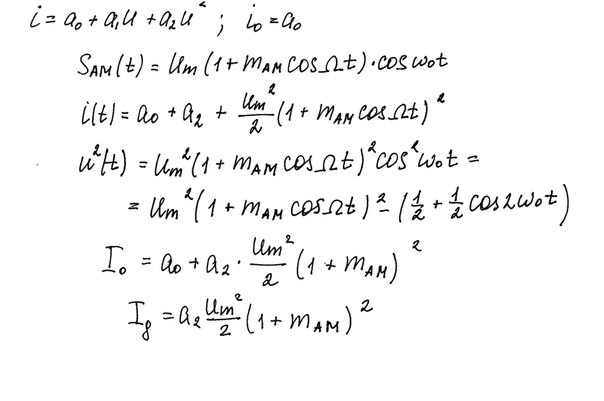
В РМА СХД квадратичная и зависит от квадрата амплитуды. Приводит к нелинейным искажениям. СХД должна быть линейна.