Циркуляция вектора в магнитного поля в вакууме
Введем, аналогично циркуляции вектора напряженности электростатического поля, циркуляцию вектора магнитной индукции. Циркуляцией вектора В по заданному замкнутому контуру называется интеграл
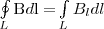
где dl — вектор элементарной длины контура, который направлен вдоль обхода контура, Bl=Bcosα — составляющая вектора В в направлении касательной к контуру (с учетом выбора направления обхода контура), α — угол между векторами В и dl.
Закон полного тока для магнитного поля в вакууме (теорема о циркуляции вектора В): циркуляция вектора В по произвольному замкнутому контуру равна произведению магнитной постоянной μ0 на алгебраическую сумму токов, охватываемых этим контуром:
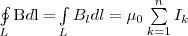 (1)
(1)
где n — число проводников с токами, которые охватываются контуром L любой формы. Каждый ток в уравнении (1) учитывается столько раз, сколько раз он охватывается контуром. Ток считается положительным, если его направление образует с направлением обхода по контуру правовинтовую систему; отрицательным считается ток противоположного направления.
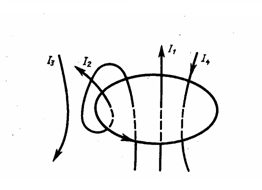
Рис.1
Например, для системы токов, изображенных на рис. 1,
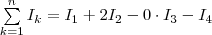
Выражение (1) выполняется только для поля в вакууме, поскольку, как будет показано дальше, для поля в веществе нужно учитывать молекулярные токи.
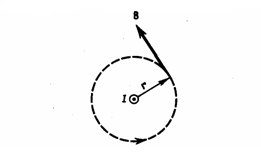
Рис.2
Продемонстрируем справедливость теоремы о циркуляции вектора В на примере магнитного поля прямого тока I, который перпендикулярн плоскости чертежа и направлен к нам (рис. 2). Возьмем в качестве контура окружность радиуса r. В каждой точке этого контура вектор Водинаков по модулю и направлен по касательной к окружности (она есть и линия магнитной индукции). Значит, циркуляция вектора В равна
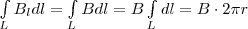
Используя формулу (1), получим В•2πr=μ0I (в вакууме), откуда
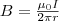
Значит, используя теорему о циркуляции вектора В мы получили выражение для магнитной индукции поля прямого тока, выведенное ранее на основании закона Био-Савара-Лапласа.
Сравнивая выражения для циркуляции векторов Е и В, можно увидеть, что между ними существует принципиальное различие. Циркуляция вектора Е электростатического поля всегда равна нулю, т. е. электростатическое поле потенциально. Циркуляция вектора В магнитного поля не равна нулю. Такое поле носит название вихревое.
Теорема о циркуляции вектора В имеет в теории о магнитном поле такое же значение, как теорема Гаусса в электростатике, поскольку дает возможность находить магнитную индукцию поля без использования закона Био-Савара-Лапласа.
