Лаплас және Бабине формулалары. Қысымның биіктік бойынша жергілікті өзгеруі

Лапластың барометрлiк формуласы. Лапластың барометрлiк формуласы статиканың негiзгi теңдеуiнiң жеке шешiмдерiнiң бiрi болып табылады. Ол формулада ауаның ылғалдылығы, температураның биiктiк бойынша әртүрлi таралуы және еркiн түсу үдеуiнiң биiктiк пен ендiкке бағыныштылығы ескерiледi. Лапластың барометрлiк толық формуласы:

z₂ – z₁ = 18400(1+a )(1+0,378 )(1+0,0026cos2j)

(1+3,09*10^-7 z) lg , (2.35)

мұнда: p₁ және p₂ – z₁ және z₂ деңгейлерiндегi атмосфера

қысымы;

18400 – барометрлiк тұрақты; a = 0,0037 » 0,004;

– екi деңгейдiң арасындағы орташа температура;

e/p – екi деңгейдiң арасындағы орташа парциалды қысым мен орташа ауа қысымының қатынасы;

j – географиялық ендiк;

z = (z₁ + z₂)/2 – екi деңгейдiң теңiз деңгейiнен орташа биiктiгi;

Бұл барометрлiк формуламен екi пункттiң биiктiк аралығын дәл анықтауға (барометрлiк нивелирлеу) болады. Бiрақ, көбiне метеорологиялық есептердi шешкенде бұндай жоғары дәлдiк қажет емес, сондықтан да практикада Лапластың барометрлiк қысқаша формуласы кең қолданылады:

z₂ – z₁ = 18400(1+a )lg . (2.36)

Бұл формуланы натурал логарифмге және абсолюттiк температураға келтiрiп былайша жазуға болады:

, (2.37)

мұнда: = 273(1+a ) – екi деңгейдiң арасындағы орташа

барометрлiк температура.

Бабиненiң барометрлiк формуласы. Егер екi деңгейдiң биiктiк айырмашылығы онша үлкен болмаса Бабиненiң барометрлiк формуласын қолдануға болады:

. (2.38)

Бұл формула барлық барометрлiк формулалардың iшiнде ең қарапайымы болып есептеледi және оның қателiгi Dz = 1000 метр болғанда ± 0,1%, ал Dz = 2000 метр болғанда ± 0,4 % құрайды.

Статиканың негiзгi теңдеуi, қозғалыссыз тыныштықтағы атмосфера қысымының биiктiк бойынша өзгеру заңын сипаттайды. Бiрақ, шынайы қозғалыстағы атмосфера үшiн де статиканың негiзгi теңдеуiнiң шешiмдерi жоғары дәлдiкпен орындалады.

Қысымның биiктiк бойынша өзгерiсiн қарастырғанда жоғарыда айтылған қысымның вертикальдi градиентi мен қысым сатысы ұғымдарын қолдануға болады.

Қысымның вертикальдi градиентi (G) деп – бiрлiк биiктiкке (100 м) көтерiлгенде қысымның өзгеру мәнiн айтады. Өлшем бiрлiгi – гПа/100 м. Ол статиканың негiзгi теңдеуiнен шығады:

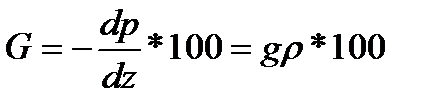. (2.20)

Ауа тығыздығы iс жүзiнде өлшенбейдi, газ күйi теңдеуiмен есептелiп табылатынын бiз бiлемiз. Сонда 2.15 теңдеуiндегi r-нiң мәнiн 2.20 теңдеуiне қойсақ табамыз:

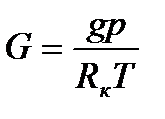*100 . (2.21)

Қалыпты жағдайда теңiз деңгейiндегi (r = 1,29 кг/м²; g = 9,81 м/с²; P = 1000 гПа; R_к = 287 м²/с²К; T = 273 К) вертикальдi қысым градиентi мәнiн табуға болады:

G = 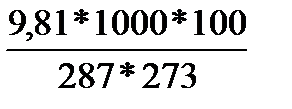= = 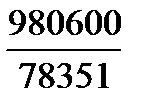12,5 гПа/100м.

Сонымен теңiз деңгейiнде 100 м биiктiкке көтерiлгенде ауа қысымы 12,5 гПа-ға азаяды екен. Бұл градиент мәнi температура мен қысымға байланысты өзгерiп тұрады, яғни биiктеген сайын G азая бередi.

Егер еркiн түсу үдеуiн тұрақты деп алсақ 2.21 теңдеуiн былай жазса да болады:

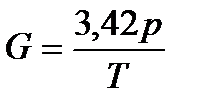*100 . (2.22)

Қысымның вертикальдi градиентi қысымға тiке пропорционал, температураға керi пропорционал. Жер бетiнен биiктеген сайын ауа қысымы азаятындықтан, қысымның вертикальдi градиентi де азая түседi. Ал, оның температураға бағыныштылығын ескерсек, жылы ауада (температура өскенде) қысым градиентi салқын ауаға қарағанда (статиканың негiзгi теңдеуiнiң 3-шi қорытындысына сәйкес келедi) төмен болады.

Қысым сатысы (h)деп – ауа қысымын 1 гПа-ға азайту үшiн көтерiлуге керектi биiктiк мәнiн айтады. Өлшем бiрлiгi – м/гПа. Ол қысымның вертикальдi градиентiне керi көрсеткiш және статиканың негiзгi теңдеуiнен (2.17) шығады:

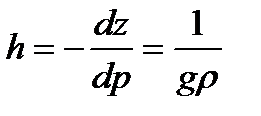немесе 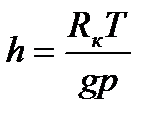. (2.23)

Қысым сатысы вертикальдi градиентпен былай қатынаста: h = 100 / G. (2.24)

Егер, еркiн түсу үдеуiнiң кiшiгiрiм өзгерiсiн ескермесек, қысым сатысы тек ауа тығыздығына бағынышты болады. Ал, атмосфераның жоғарғы қабаттарына көтерiлген сайын ауа тығыздығы азаятындықтан қысым сатысы өсе түседi. Бiрдей қысым кезiнде қысым сатысы салқын ауаға қарағанда жылы ауада үлкен болады.

Есептеудi оңайлату үшiн 2.23 теңдеуiн мынадай қарапайым түрге келтiрсе де болады:

,

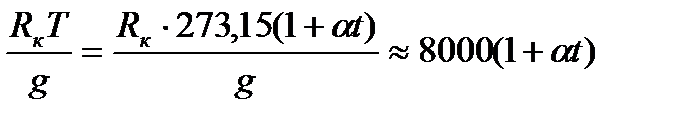яғни 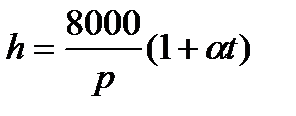, (2.25)

мұнда: a = 0,0037 – ауаның температуралық ұлғаю коэффициентi.

Қалыпты жағдайда теңiз деңгейiнде (p=1000гПа; t=0⁰С) жерге жақын ауа қабатында қысым сатысы 8 м/гПа-ға тең болады. Яғни ауа қысымы 1 гПа-ға төмендеу үшiн жер бетiнен 8 м биiктiкке көтерiлу қажет. Қысымы шамамен 500 гПа 5 км биiктiкте сол 0⁰С жағдайында қысым сатысы 16 м/гПа шамасында болады. Яғни, жерден биiктеген сайын қысым сатысы да өсе түседi екен.

Қысым сатысы температураға да бағынышты. Ауа температурасы өскен сайын, қысым сатысы әр 1⁰С сайын шамамен 0,4%-ға өсiп отырады. Сондықтан қысым сатысы жылы ауада жоғары болады, салқын ауаға қарағанда. Яғни, жылы ауада қысым 1гПа төмендеу үшiн көбiрек биiктiкке көтерiлу керек және де жерден биiктеген сайын ол одан сайын өсе түседi. Нәтижесiнде жылы ауада қысым биiктiк бойынша салқын ауаға қарағанда жайырақ төмендейдi. Сондықтан да, бiрдей биктiкте қысым жылы ауаның үстiнде салқын ауаға қарағанда жоғарырақ болады.