Приклади розв'язання задач
Задача 5.1. Два мильних пузирі радіусами R1 = 2 см та R2 =3 см зливаються в один. Визначити енергію, що виділяється при цьому процесі, якщо коефіцієнт поверхневого натягу 0,045 Н/м.
Рішення. Оскільки поверхня двох пузирів більша за поверхню пузиря, що утворився внаслідок злиття їх в один, частина енергії поверхневої плівки звільняється. Відомо, що при ізотермічному зменшенні поверхні рідини на один квадратний метр буде виділятися енергія, що чисельно дорівнює коефіцієнту поверхневого натягу рідини. Таким чином, для знаходження енергії, яка виділиться при злитті двох пузирів в один, необхідно визначити, на яку величину їх поверхня була більша поверхні новоутвореного пузиря. Зовнішня поверхня двох пузирів до їх злиття буде
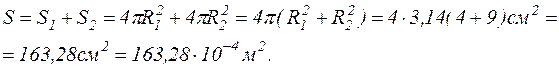
Для визначення зовнішньої поверхні пузиря, що утворився внаслідок злиття двох пузирів, потрібно знайти радіус новоутвореного пузиря, який можна визначити з рівності об'ємів пузирів до та після їх злиття, тобто
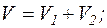
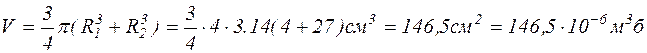звідки шуканий радіус
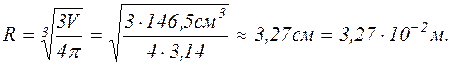
Поверхня нового пузиря
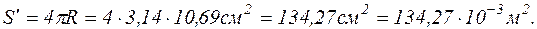
Зменшення зовнішньої поверхні
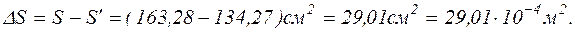
Оскільки пузир має дві поверхні, то повне зменшення поверхні буде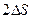 
. Енергія, що виділилася при утворенні нового пузиря, буде
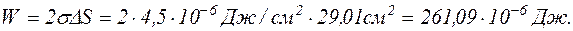
Відповідь:261,09×10-6 Дж.
Задача 5.2.Визначити діаметр капілярів у папері, якщо вода піднімається в ньому на висоту Н = 30 см, а коефіцієнт поверхневого натягу води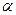 
= 0,07 Н/м.
Рішення.Висоту підняття рідини в капілярі знаходять за формулою
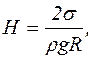
звідки діаметр капілярів
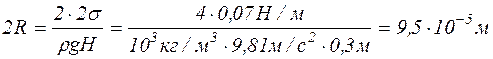
Відповідь: d = 9,5×10-5 м.
Задача 5.3.Який тиск водяної пари поблизу краплі води, радіус якої R = 5×10-6 см, при температурі t = 10 °С, якщо коефіцієнт поверхневого натягу води при 20 °С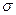 
= 7,3×10-2 Н/м?
Рішення. Крапля води має опуклу поверхню, внаслідок чого додатковий молекулярний тиск поверхневої плівки спрямовано в середину краплі, а це ускладнює "випаровування'' молекул. З рідини вилітають молекули, які мають більшу кінетичну енергію, а значить, і більшу швидкість, а тому і тиск пари над опуклою поверхнею буде більший, ніж над плоскою та ввігнутою.
Зі збільшенням кривизни поверхні тиск пари теж збільшується.
Тиск пари біля поверхні водяної краплі знаходимо за формулою
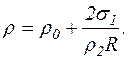
Тиск насиченої пари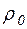 
, густину насиченої пари 
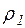та рідини 
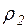знаходимо з таблиць, а коефіцієнт поверхневого натягу при 10 °С - за формулою
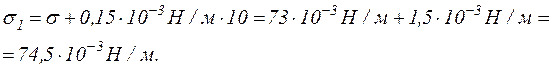
Підставляючи у формулу тиску пари числові значення величин, знаходимо
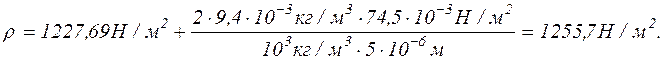Відповідь: 
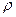= 1255,7 Па.
Задача 5.4. Вода подається у фонтан із широкої посудини І та виходить із отвору II зі швидкістю 12 м/с. Діаметр посудини дорівнює 2 м, діаметр перерізу II дорівнює 2 см.
Знайти: 1) швидкість зниження рівня води у посудині; 2) тиск, під яким вода подається у фонтан; 3) висоту рівня h1 води в посудині і висоту h2 струменя води, яка виходить із фонтану.
Рішення.1. Проведемо поперечний переріз І у посудиш на рівні перерізу II фонтану. Оскільки площа S1 перерізу І набагато більша площі S2 перерізу II, тоді висоту h1 рівня води в посудині можна вважати для малого проміжку часу сталою, а потік - сталий.
Для сталого струменя води справедлива умова нерозривності потоку v1S1=v2S2, звідки знаходимо, що
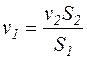або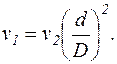 
Підставляючи у цю формулу числові значення величин, взятих в одиницях системи СІ та виконавши обчислення, знайдемо
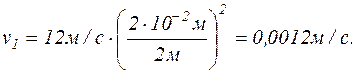
З такою ж швидкістю буде знижуватися рівень води у посудині. Як бачимо, ця швидкість набагато менша порівняно зі швидкістю струменя води.
2. Тиск 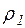, під яким вода подається у фонтан, знайдемо з рівняння Бернуллі. У випадку течії в горизонтальній трубці воно має вигляд
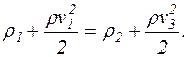
Враховуючи, що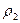 
= 0 (під цим тиском розуміють надлишковий над атмосферним тиском), з рівняння Бернуллі отримаємо
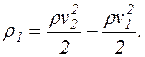
Оскільки v1<<v2, маємо
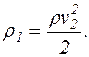
Підставляючи числові значення величин, взятих в одиницях системи Сі. знаходимо
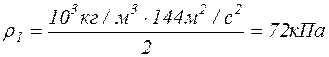
3. Висоту h1 рівня води у посудині знайдемо із співвідношення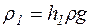 
, звідки
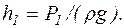
Підставляючи в останню формулу числові значення величин, взятих в одиницях системи СІ та обчислюючи, маємо
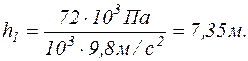
Знаючи швидкість v2, з якою вода викидається фонтаном, знайдемо висоту h2, на яку вона буде підніматися:
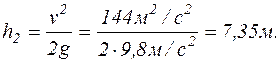
Підкреслимо, що висота рівня води у посудині дорівнює висоті, на яку піднімається фонтан води.
Відповідь: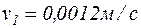 
; 
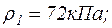h1=7,35м; h2=7,35м.
Запитання для самоконтролю
1. Яка енергія називається вільною енергією поверхневої плівки рідини та як вона обчислюється?
2. Що таке крайовий кут та яке його значення у випадках повного змочування та незмочування?
3. Які факти впливають на зміну рівня рідини в капілярі та як обчислюється висота рівня?
4. Чи змінюється рівень води в капілярі, якщо його нахилити?
5. Як тиск насиченої пари залежить від кривизни поверхні рідини?
6. Чим відрізняється ідеальна рідина від реальних рідин?
7. Які течії вважаються подібними?
8. Який фізичний зміст числа Рейнольдса?
9. Який фізичний зміст числа Фрунда – F2=v 2/gl?
10. Яку швидкість називають критичною?