Ширина интерференционной полосы

Из (2.5) следует, что в точке расположен максимум, соответствующий нулевой разности хода. Для него порядок интерференции . Это центр интерференционной картины. При переходе к соседнему максимуму 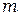меняется на единицу и — на величину .Расстояние между двумя соседними максимумами (или минимумами) называетсяшириной интерференционной полосы.Из формулы (2.5) или (2.6) легко получить:

.

Отсюда следует, что ширина интерференционной полосы определяется выражением:

(2.7)

Согласно формуле (2.7), расстояние между полосами растёт с уменьшением расстояния между щелями 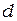и с увеличением расстояния до экрана 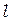. При 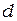, сравнимом с 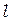, расстояние между полосами было бы одного порядка с 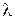, и составляло бы несколько десятка мкм. В этом случае отдельные полосы были бы совершенно неразличимы, поскольку разрешающая способность глаза ≈ 0,1мм, а длина волны света ≈ 0,5мкм, т.е. на три порядка меньше. Для того чтобы интерференционная картина стала отчётливой, необходимо соблюдение упоминавшегося выше условия .

Период, положение и контрастность интерференционных полос зависят от основных параметров источников излучения: их длины волны (или частоты), начальной фазы, соотношения амплитуд, а также от взаимного расположения источников. Проследим это влияние на модельных экспериментах.

Влияние расстояния между источниками излучения на интерференционную картину продемонстрировано на рис. 2.5.

Рис. 2.5. Влияние расстояния между источниками на ширину интерференционных полос: в случае (а) расстояние в два раза больше, чем в случае (б).

На этом рисунке полосы от двух точечных источников в области чередования тёмных и светлых участков (гребней и впадин волн) соответствуют максимумам интерференционной картины, а расходящиеся веером серые полосы — интерференционным минимумам. Как и следует из формулы для ширины интерференционной полосы (2.7), при сближении источников (рис. 2.5б) период интерференционной картины возрастает.

Изменение длины волны источников моделируется на рис. 2.6. При неизменном расстоянии между ними с увеличением длины волны (рис. 2.6б) ширина интерференционной полосы возрастает, чтобы набрать прежнюю разность хода, теперь нужно большее расстояние.

Рис. 2.6. Влияние длины волны на ширину интерференционных полос:

в случае (а) длина волны в два раза меньше, чем в случае (б).

Введём в рассмотрение угол - угол, под которым видны щели S₁ и S₂ из центра интерференционной картины. Из рис. 2.7 видно, что , поэтому формулу для ширины интерференционной полосы (2.7) можно переписать в виде:

. (2.8)

	y

Рис. 2.7

Таким образом, ширина интерференционной полосы пропорциональна длине волны 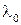и обратно пропорциональна углу, под которым видны источники волн из центра интерференционной картины.

2.2. Распределение интенсивности

Рассмотрим идеализированный случай, когда два одинаковых источника 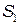и 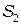в опыте Юнга строго монохроматические. В интересующую нас точку экрана колебания от этих источников будут приходить практически с одинаковой амплитудой . Тогда согласно формуле (1.3)

, (2.9)

где 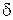— разность фаз. Последнее выражение записано, используя формулу половинного угла из тригонометрии .

Разность фаз согласно формуле (1.14) равна .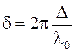

Поскольку интенсивность , из (2.8)получим:

, (2.10)

где - порядок интерференции.

Из формулы следует, что если интерференция наблюдается, то интенсивность в максимумах равна при значении , а в минимумах при . При отсутствии интерференции , так как

Рис. 2.8. Распределение интенсивности на интерференционной картине
от двойной щели в случае монохроматической волны.

Естественно, что показанное на рис. 2.8 идеализированное распределение интенсивности существенно отличается от реального. Эти отличия обусловлены: во-первых, степенью монохроматичности и степенью пространственной когерентности используемого света, и, во-вторых, дифракционными явлениями.

В случае белого света интерференционная картина от двойной щели представляет собой чередование тёмных и разноцветных полос, параллельных друг другу (Рис. 2.9.).

Центральная полоса или нулевой максимум ( ) белого цвета, поскольку соответствует нулевому сдвигу фаз для всех компонент белого света. Остальные максимумы разложены в спектр. Но, начиная со второго максимума, интерференционные полосы перекрываются и далее исчезают.

Рис. 2.9.

Появление разноцветных полос, очевидно, связано с тем, что условия интерференции (1.16 и 1.18) для различных частотных компонентов белого света соблюдаются в пространственно различных точках экрана ( и ). Чем больше длина волны, тем дальше от центра располагается максимум или минимум для данной длины волны.

Из формулы ширины интерференционной полосы (2.7) следует, что:

. (2.11)

Измерив, расстояние между полосами , а также расстояние от щелей до экрана 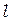и расстояние между центрами щелей 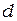можно вычислить 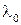. Именно из опытов по интерференции света впервые Юнгом были определены длины волн для световых лучей разного цвета.

КОГЕРЕНТНОСТЬ

При объяснении явления интерференции важным понятием является понятие когерентности света. Исторически оно возникло в связи с интерференционными опытами. Появление интерференционной картины в опыте Юнга (и в других опытах) зависит от того, какой свет падает на экран с двумя точечными отверстиями.

Если это свет точечного источника, каковым является маленькое отверстие в экране S или узкая щель, то интерференция есть. Если же это свет от протяженного источника или свет, рассеянный матовой пластинкой, то интерференции нет. Способность света давать интерференционную картину называют когерентностью. Когерентность связана со структуройсвета: когерентный свет — это свет, структура которого близка к плоской или сферической гармонической волне. Про такой свет говорят, что он имеет высоко упорядоченную структуру. Понятию когерентности соответствует понятия: «согласование», «корреляция». В противоположность этому некогерентный свет — это свет, не способный давать интерференциюи подчиняющийся закону сложения интенсивностей. Такой свет представляет собой случайно модулированную волну, т.е. волну, у которой амплитуда и фаза описываются случайными функциями.

Монохроматические волны считаются когерентными, если они имеют одинаковые частоты, а разность фаз между ними остается неизменной с течением времени. Такие волны интерферируют. Подчеркнем, что интерференция имеет место для волн одинаковой поляризации.

3.1. Временная когерентность. Длина когерентности

Различают временную и пространственную когерентность или, в других терминах, различают длину и ширину когерентности. Понятие временной когерентности (или длины когерентности) связано со степенью монохроматичности света, поскольку идеального монохроматического света не существует. В опыте Юнга интерференционная картина по мере удаления от её середины размывается, видны несколько полос, но далее постепенно они исчезают. Очевидно, это связано с тем, что степень когерентности складываемых в этих точках экрана волн постепенно уменьшается, по мере увеличения разности хода между ними.

Например, мы наблюдаем четыре порядка интерференции (4 полосы - ), а затем полосы исчезают. Исчезновение полос с 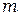>4 означает, что, пока разность хода между волнами , волны когерентны (этот вывод следует из условия минимумов и максимумов). Это значит, что вдоль распространения волны когерентными между собой будут только участки волны в этом интервале 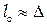. Данный интервал и называется длиной когерентности 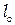. В рассматриваемом случае . Заметим, что в данных условиях это простейший способ оценки длины когерентности:

, (3.1)

где - максимальный порядок интерференции, соответствующий ещё видимой светлой полосе. Всё это можно схематически представить с помощью рис. 3.1.

Свет, падающий на обе щели, имеет какую - то длину когерентности . Обе щели создают две волны с такой же длиной когерентности, но, поскольку они достигают разных точек экрана с различными разностями хода, то участки когерентности обеих волн постепенно сдвигаются относительно друг друга и, начиная с , перестают перекрывать друг друга.

Рис. 3.1

Складываемые волны перестают быть когерентными, и интерференционные полосы исчезают. Всё сказанное справедливо при условии, что «первичная» щель достаточно узка. При расширении щели вступает в действие другой эффект, связанный с пространственной когерентностью (шириной интерференции).

Найдём выражение, определяющее . Известно, что строго монохроматический свет – это идеализация. Реальный свет остаётся в той или иной степени немонохроматическим, представляющим собой набор монохроматических компонент в некотором конечном интервале длин волн ( ). Будем считать, что монохроматические компоненты равномерно заполняют этот интервал.

Как показывает формула (2.1) ширина интерференционной полосы пропорциональна 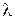(без более тонких деталей). Изобразим положение максимумов для длин, соответствующих крайним значениям спектрального интервала ( ), сплошными отрезками – для 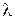, пунктирными для - . Максимумы же промежуточных длин волн заполняют интервал между крайними максимумами каждого порядка интерференции. В результате промежуточные максимумы, как видно из рисунка, будут постепенно размываться, и полосы постепенно исчезнут.

С помощью рисунка рис. 3.2 можно заключить, что полосы исчезнут при таком максимальном значении 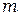, где 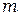-ый максимум самой длинной волны совпадёт с ( ) - максимумом более короткой волны:

,

здесь 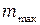- предельный порядок интерференции, начиная с которого полосы исчезают. Отсюда максимальный порядок интерференции:

. (3.2)

Величина характеризует степень монохроматичности света: чем она больше, тем больше и степень монохроматичности, тем больше чётких максимумов наблюдается на интерференционной картине.

Рис. 3.2

Таким образом, мы нашли то значение 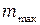, при котором интерференция исчезает, т.е. складываемые колебания становятся уже не когерентными. Заметим, что установить точное значении 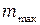затруднительно из-за того, что полосы размываются и исчезают постепенно.

Найденное значение 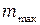(3.2) связано с длиной когерентности (3.1) как . Отсюда следует, что

. (3.3)

Мы видим, что длина когерентности световой волны непосредственно связана со степенью монохроматичности ( ): чем больше последняя, тем больше и длина когерентности, тем больше наблюдается максимумов на интерференционной картине. Для солнечного света , для лучших (не лазерных) источников удалось получить порядка несколько десятков сантиметров. Лазеры позволили получить излучение с порядка сотен метров (и даже нескольких километров)!

Отсюда следует, что для получения интерференционной картины необходимо, чтобы оптическая разность хода складываемых волн была меньше длины когерентности: .

В заключение заметим, что длина когерентности связана с так называемым временем когерентности - промежутком времени, в течение которого случайные изменения фазы световой волны достигают значения порядка .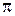

На примере интерференции от двух щелей понятие временной когерентности можно интерпретировать следующим образом. Каждая частотная компонента, присутствующая в спектре света, создает в пространстве свою интерференционную картину — периодические полосы. Результирующую картину интенсивности в плоскости наблюдения можно рассматривать как результат сложения этих распределений. Распределения, созданные различными частотными компонентами, будут иметь различную пространственную периодичность. Поэтому с увеличением времени задержкимежду двумя пучками интерференционная картина будет становиться все менее и менее различимой, так как минимумы одного распределения будут налагаться на максимумы другого. В результате картина окажется однородной, так как в ней не будет выраженных максимумов и минимумов интенсивности, т.е. интерферограмма не формируется. Это происходит, когда время задержки становится больше времени когерентности ( ), и интерференционные полосы исчезают.

3.2. Пространственная когерентность. Ширина когерентности

Понятие «точечный источник» — это такая же идеализация, как и монохроматическая волна. Все реальные источники являются протяженными, а это приводит к уменьшению контраста интерференционной картины. Опыт показывает, что при увеличении размеров источника видимость интерференционной картины постепенно уменьшается и при достаточно больших размерах интерференционные полосы полностью исчезают. Качественно характер изменения видимости полос при увеличении размеров источника можно понять, если предположить, что протяженный источник состоит из независимых излучателей (Рис. 3.3).

Рис.3.3. Интерференция от протяженного источника.

Действительно, весь источник света можно «разбить» на малые площадки с линейным размером много меньше длины волны, состоящие из атомов, излучающих независимо от атомов другой площадки , поэтому волны, излучаемые этими площадками, являются некогерентными и интерференции между ними не будет.

Этот же случай можно рассмотреть на примере с двойной щелью. До сих пор щель 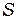в опыте Юнга, по умолчанию, предполагалась весьма узкой (часто говорят бесконечно узкой). Расширение же щели, как и уменьшение степени монохроматичности света, приводит к ухудшению (размытию) интерференционных полос и даже к полному их исчезновению. Чтобы выяснить роль ширины щели ,рассмотрим теперь на примере опыта Юнга другой крайний случай: излучение монохроматическое, щель не узкая.

Интерференционную картину на экране (рис. 3.4 и рис. 3.5) можно представить как наложение интерференционных картин от бесконечно узких щелей, на которые мысленно разобьём щель .

Рис. 3.4 Рис. 3.5

Пусть положение максимумов на экране от узкой щели, взятой около верхнего края щели – точки 1— таково, как отмечено сплошными отрезками на рис. 3.4. А максимумы от узкой щели, взятой около нижнего края щели — точки 2, будут смещены вверх, они отмечены пунктирными отрезками на этом же рисунке. Интервалы между этими максимумами заполнены максимумами от промежуточных узких щелей, расположенных между краями 1и 2.

При расширении щели расстояния между максимумами от её крайних элементов будут увеличиваться, т. е. интервалы между соседними максимумами от одного края щели будут постепенно заполняться максимумами от остальных элементов щели.

Для простоты будем считать, что в схеме (рис. 3.5) расстояния . Тогда при ширине щели ,равной ширине интерференционной полосы ( ), интервал между соседними максимумами от края 1будет целиком заполнен максимумами от остальных элементов щели, и интерференционные полосы исчезнут.

Итак, при расширении щели интерференционная картина постепенно размывается и при некоторой ширине щели практически исчезает.

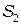Это наблюдаемое явление можно объяснить и иначе, а именно: интерференционная картина исчезает вследствие того, что вторичные источники – щели и становятся некогерентными. Сказанное позволяет говорить о ширине когерентности падающей на щели S₁ и S₂ световой волны – ширине , на которой отдельные участки волны в достаточной степени когерентны и дают интерференционную картину. Во избежание недоразумений уточним: под шириной когерентности понимается характерное для данной установки расстояние между точками поверхности, перпендикулярной направлению распространения волны.

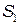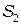Найдём формулу для вычисления . В рассматриваемой схеме опыта Юнга очевидно, что минимальная ширина когерентности падающей волны не может быть меньше расстояния между щелями , т.е. условие, при котором щели и становятся когерентным, есть следующие:

, (3.4)

где - расстояние между щелями. Кроме того, мы выяснили, что интерференционная картина исчезнет когда, когда ширина первичной щели 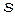равна ширине интерференционного максимума (т.е. условие, при котором щели становятся не когерентными):

. (3.5)

Ширина интерференционного максимума, согласно формуле (2.7), равна . Из этих трёх равенств получим:

, (3.6)

где 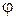- угловая ширина щели 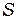относительно диафрагмы с двумя щелями. Итак, ширина когерентности

. (3.7)

Таким образом, ширина когерентности пропорциональна длине волны и обратно пропорциональна угловой ширине источника относительно интересующего нас места (в опыте Юнга – относительно места расположения двух щелей). Сказанное поясняет рис. 3.6.

Рис. 3.6

Если в качестве источника использовать непосредственно Солнце (его угловой размер рад и мкм.), то ширина когерентности, согласно (3.6), мм. Для получения интерференционной картины от двух щелей с помощью такого излучения расстояние между двумя щелями должно быть меньше 0,05 мм, что сделать практически невозможно.

Из сказанного в предыдущем разделе следует, что временная когерентность связана с разбросом значений 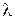, и, следовательно, с разбросом значений модуля волнового вектора , где 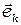единичный вектор, совпадающий с направлением распространения световой волны. Пространственная когерентность связана с разбросом направлений вектора 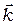, который характеризуется величиной .

Формула (3.4) по существу лежит в основе метода, предложенного Физо и осуществленного Майкельсоном, по определению угловых размеров звёзд путем измерения ширины когерентности. Попытки провести эти измерения, помещая экран с двумя щелями перед объективом телескопа, оказались безуспешными: полосы интерференции оставались четкими даже при наибольшем расстоянии между этими щелями. Майкельсон преодолел эту трудность с помощью звездного интерферометра (рис. 3.7). Расположенные против щелей зеркала – — неподвижны, а зеркала — можно одновременно раздвигать, меняя расстояние 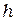между ними. Видимость полос зависит от степени когерентности световых колебаний на зеркалах — , в то время как ширина полос определяется расстоянием между щелями. Постепенно раздвигая зеркала — , обнаруживают, что при определенном расстояниимежду ними интерференционная картина исчезает. Это значит, что расстояние между этими зеркалами оказалось таким, что . Остается по формуле (3.4.) вычислить 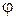. При максимальном расстоянии м. можно было измерить угловой диаметр объекта угл. сек.

Рис. 3.7

Первой звездой, угловой диаметр которой удалось определить, была Бетельгейза (0,047 угл. сек.). Измерив, кроме того, расстояние до неё (по параллаксу), определили диаметр этой звезды-гиганта (он оказался больше диаметра земной орбиты!).

Объём когерентности.Всё пространство, занимаемое волной, можно разбить на части, в каждой из которых волна приблизительно сохраняет когерентность. Объём такой части пространства, называемой объёмом когерентности, по порядку величины равен произведению длины когерентности 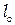на площадь круга, радиуса равного ширине когерентности

. (3.5)

Общие выводы.Для получения устойчивой интерференционной картины с использованием обычных (не лазерных) источников света необходимо исходную световую волну расщепить подходящим способом на две части, которые затем в области перекрытия и дадут систему полос, но лишь в том случае, если у исходной световой волны:

1) длина когерентности 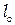превышает оптическую разность хода 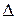складываемых колебаний и

2) ширина когерентности превышает расстояние между щелями.

Насколько больше должны быть эти величины общепринятого соглашения нет. Будем считать, например, вдвое. Тогда можно записать:

(3.6)

. (3.7)

Выполнение этих условий гарантирует получение интерференционной картины с достаточно хорошей видимостью полос.

ПОЛОСЫ РАВНОГО НАКЛОНА

Рассмотрим интерференцию в тонких пластинках. Пусть из воздуха ( = 1) на плоскопараллельную прозрачную пластинку с показателем преломления 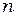и толщиной 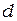под углом 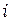падает плоская монохроматическая волна (рис.4.1а).

Рис. 4.1

В точке О луч частично отразится (1), а частично преломится и, после отражения на нижней поверхности пластины в точке С, выйдет из пластины в точке В (2). Вообще, в случае плоской пластинки будет наблюдаться многократное отражение и преломление от внутренних поверхностей пластинки, но мы этим пренебрежём из-за слабой интенсивности этих многократно отражённых лучей. Лучи 1 и 2 параллельны и с помощью собирающей линзы их можно свести в точке Р.

Необходимо отметить важную особенность отражения электромагнитных волн (и в частности, оптических лучей) при падении их на границу раздела двух сред из среды с меньшей диэлектрической проницаемостью. При отражении света от более плотной среды ( < 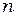) фаза изменяется на 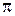. Изменение фазы на 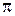равносильно потере полуволны при отражении.

Такое поведение электромагнитной волны на границе двух сред следует из граничных условий, которым должны удовлетворять тангенциальные компоненты векторов напряженности электрического и магнитного поля на границе раздела: , . С учетом этого оптическая разность хода:

.

Из рис. 4.1 видно, что и

.

Последнее выражение записано, используя закон преломления .

или

. (4.1)

Так как , то в итоге получаем формулу, определяющую разность хода между отражённой и преломлённой волной на тонкой пластинке:

. (4.2)

Если отражённые волны 1 и 2 (рис. 4.1б)когерентны между собой, то в точке наблюдения будут наблюдаться максимумы отражения при условии:

. (4.3)

В точке будет интерференционный минимум, если

, (4.4).

где - целое число (порядок интерференции).

Меняя угол падения, мы будем наблюдать последовательную смену максимумов и минимумов отражения. (Заметим, что при минимуме отражения наблюдается максимум проходящего через пластинку света, и наоборот.) Если бы обе отражённые волны были некогерентными, то такого явления мы не наблюдали бы: по мере увеличения угла падения интенсивность отраженного света монотонно уменьшалась бы.

Теперь выясним условия, при которых отражённые волны будут когерентными и смогут интерферировать. В предыдущем разделе мы установили, что для этого должны выполняться соотношения между длиной когерентности и разностью хода:

(3.6)

. (3.7)

Здесь - расстояние между щелями в опыте Юнга, т.е. источниками вторичных волн. Для нашего случая под нужно понимать поперечное смещение между отражённым и преломлённым лучами (расстояние AB на рис.4.1).

Проиллюстрируем ситуацию с помощью рис. 4.2. Выделим в падающей волне некоторую область когерентности (она слегка затенена на рисунке) и проследим за её дальнейшей судьбой. После расщепления падающей волны расщепится и выделенная область когерентности, причем так, что в отражённых волнах эти области когерентности сместятся относительно друг друга (рис.4.2а). Если они при этом перекрываются (на рисунке более тёмный участок), интерференция будет наблюдаться и тем более отчетливо, чем больше степень перекрытия.

Нетрудно заметить, что для пластинки с большей толщиной область перекрытия когерентных участков уменьшается (рис. 4.2б), и интерференция будет наблюдаться все менее отчетливо. Начиная с некоторой толщины пластинки, интерференция исчезнет совсем.

Рис. 4.2

Из рис. 4.2 видно, что смещение расчленённых частей области когерентности происходит как вдоль распространения волны (оно не должно превосходить длину когерентности ), так и поперёк распространения волны (смещение не должно превосходить ширину когерентности ). Интерференция будет наблюдаться лишь в том случае, когда будут удовлетворены оба эти условия. Напомним, что для лучшей видимости мы договорились брать половины значений и . Перейдем к расчёту. Согласно (3.6) , необходимо, чтобы оптическая разность хода . Следовательно,

.(4.5)

Для оценки необходимого значения толщины пластинки 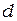будем считать, что корень в этом выражении равен величине порядка единицы (что обычно и бывает), а также пренебрежем 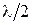. Тогда получим

, (4.6)

т. е. необходимо, чтобы удвоенная толщина пластинки была не более половины длины когерентности используемого излучения. Например, если 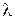= 600 нм, а 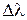= 3 нм, то толщина пластинки

.

Далее, поперечный сдвиг частей области когерентности не должен превосходить половины ширины когерентности . Этот сдвиг, как видно из рис. 4.1, равен отрезку АВ. Значит, необходимо, чтобы .Из рис. 4.1 следует, что

.

Видно, что это смещение существенно зависит от угла падения 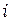. Чем меньше угол падения, тем меньше смещение , тем меньше может быть . И основную роль в этом случае будет играть длина когерентности. При смещение происходит только вдоль распространения волн, поперёк — оно равно нулю, и ширина когерентности , становится практически не существенной.

Обратимся к вопросу, что следует понимать под словами тонкая пластинка. Когда говорят, что интерференция происходит при отражении от тонкой пластинки, то имеют в виду, что её толщина (в той или иной степени) меньше и (если ). Причем — это важно — при нормальном падении интерференция обеспечивается только соотношением между толщиной пластинки и . Для солнечного света ( ) пластинка будет тонкой, если ее толщина порядка нескольких длин волн. Длину когерентности можно увеличить с помощью светофильтров, соответственно увеличивается и толщина пластинки, которую мы называем тонкой. Для лазерного же излучения тонкой будет пластинка в десятки сантиметров и метров (в зависимости от длины когерентности излучения используемого лазера).

Из формул (4.3) и (4.4) следует, что при падении плоской световой волны на плоскопараллельную тонкую пластинку интенсивность отражённого света зависит от угла падения. Изменяя этот угол, мы будем наблюдать чередование максимумов и минимумов отражённого света. Это можно использовать для получения интерференционной картины в виде привычной системы полос. Достаточно использовать в качестве падающего рассеянный монохроматический свет (он содержит волны, падающие на пластинку одновременно под разными углами), а на пути отраженного света поставить линзу и в ее фокальной плоскости экран (рис.4.3).

Рис. 4.3

Максимумы на экране будут располагаться в местах, соответствующих условию (4.3)

.

Полоса данного порядка интерференции обусловлена светом, падающим на пластинку под одним и тем же углом 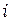, но с разных направлений. Поэтому такие полосы называют полосами равного наклона. При расположении линзы как показано на рис. 4.3, эти полосы имеют вид концентрических колец с центром в ее фокусе F.

Порядок интерференции 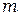растёт с уменьшением угла падения 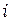, и в центре картины он максимален.Поскольку для наблюдения интерференционной картины в данном случае экран помещают в фокальной плоскости линзы, т. е. так, как его располагают для получения на нем изображения бесконечно удаленных предметов, то говорят, что полосы равного наклона локализованы в бесконечности. Роль линзы и экрана может играть хрусталик и сетчатка глаза. В этом случае для наблюдения полос равного наклона глаз нужно аккомодировать (настраивать) так, как при рассмотрении удаленных предметов.

В белом свете интерференционные полосы окрашены. Поэтому такое явление называют цвета тонких пластинок.

ПОЛОСЫ РАВНОЙ ТОЛЩИНЫ

Клиновидные пластинки. Пусть стеклянная пластинка имеет форму клина с углом раствора , и на неё падает плоская монохроматическая световая волна. Теперь отражённые от поверхностей клина световые волны будут распространяться не в одном направлении, а под некоторым углом (рис. 5.1). Выясним, прежде всего, где будет локализована интерференционная картина. Это проще всего сделать с помощью рис. 5.2, на котором показано, что происходит с областью когерентности после расщепления волны при отражении от поверхностей клина.

Рис.5.1 Рис. 5.2

Из рисунка видно, что при небольших значения длины и ширины когерентности область перекрытия когерентных частей отраженных волн локализована, в основном, вблизи поверхности клина. Это область становится все более узкой по мере перемещения в сторону утолщения клина, постепенно исчезая совсем.

Так как разность хода лучей, отразившихся от различных участков клина, неодинакова, в области локализации интерференции появятся светлые и темные полосы, параллельные ребру клина. Каждая из таких полос возникает в результате отражений от участков клина с одинаковой толщиной, поэтому их называют полосами равной толщины. Локализованные вблизи поверхности клина интерференционные полосы можно наблюдать непосредственно глазом, фокусируя его на поверхность клина, либо с помощью линзы, сфокусированной также на поверхность клина. С помощью линзы интерференционную картину с поверхности клина можно отобразить на экран Э, расположенный в плоскости, сопряженной с поверхностью клина.

Полосы равной толщины можно наблюдать в тонкой клиновидной прослойке воздуха между поверхностями двух прозрачных пластинок. Если направление наблюдения близко к нормальному, то оптическая разность хода лучей, отраженных от поверхностей клина в месте, где ширина зазора равна 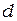, определяется как . Там, где , , возникают минимумы. Т. е. тёмные полосы возникают в тех местах, где толщина зазора . Переход от одной полосы к соседней соответствует изменению толщины зазора на . Каждая полоса соответствует определенной толщине зазора. Этот факт используют для проверки качества оптических поверхностей при их шлифовке, наблюдая в отраженном свете прослойку между контролируемой и эталонной поверхностями. Измеряя ширину полосы в монохроматическом свете с известной длиной волны 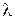, можно измерить углы порядка 0,1 угл. мин и меньше.

В предыдущих рассуждениях мы принимали во внимание только волны, отраженные от поверхностей воздушного клиновидного зазора, игнорируя волны, отраженные от наружных поверхностей пластинок. Это можно сделать лишь постольку, поскольку толщина пластинок обычно значительно превышает длину когерентности используемого света от обычных источников, и отраженные от этих поверхностей волны оказываются некогерентными.

5.1. Кольца Ньютона

Кольца Ньютона – это классический пример кольцевых полос равной толщины, наблюдаемых при отражении света от поверхностей зазора между стеклянной пластинкой и соприкасающейся с ней выпуклой линзой(рис. 5.3).

Рис. 5.3

Волна, отражённая от верхней поверхности линзы, в силу небольшойдлины когерентности обычных источников света, не когерентна с волнами, отражёнными от поверхностей зазора и участия в образовании интерференционной картины не принимает. Поэтому мы её и не будем учитывать.

Из-за радиальной симметрии линзы полосы равной толщины при нормальном падении света имеют вид концентрических окружностей с центром в точке соприкосновения. При наклонном падении – эллипсов. Интерференцию можно наблюдать и в проходящем свете, причём в проходящем свете максимумы интерференции соответствуют минимумам интерференции в отражённом свете и наоборот.

Найдем радиусы 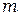-ных тёмных колец (минимумов). Сначала запишем условие образования тёмных колец. Они возникают там, где оптическая разность хода волн 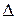, отражённых от обеих поверхностей зазора, равна нечётному числу полуволн (условие минимума ).

В случае нормального падения и формулы (4.2) следует, что в отражённом свете оптическая разность хода:

, (5.1).

где 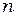- абсолютный показатель преломления материала зазора (жидкость или воздух).

Выразим величину зазора 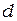через радиус линзы и радиус тёмного интерференционного кольца .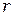

.

С учетом того, что 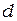мало, можно пренебречь по сравнению с . Отсюда

. (5.2)

Подставим (5.2) в (5.1) и применим условие минимума. Получим

.

Отсюда радиусы тёмных колец:

(5.3)

Аналогичный расчёт можно провести для светлых колец. Радиусы светлых колец:

(5.4)

Заметим, что значению соответствует минимум тёмного пятна (не кольца).

Следует обратить внимание на то, что формулы (5.3) и (5.4) справедливы лишь в случае идеального (точечного) контакта сферической поверхности линзы с пластинкой. Но идеальных контактов не бывает, поэтому номера колец не равны, вообще говоря, порядку интерференции 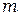, и это обстоятельство необходимо учитывать при расчётах.

Если линзу постепенно отодвигать от поверхности пластинки, то интерференционные кольца будут стягиваться к центру: это ведь кольца (полосы) равной толщины, а она при этом перемещается к центру. С помощью колец Ньютона можно с достаточно высокой точностью контролировать качество изготовления, например, сферических поверхностей.

Рассмотрим теперь на конкретном примере вопрос, связанный с причиной локализации колец Ньютона в очень малой области для обычных линз (кольца приходится рассматривать в микроскоп).

Пусть двояковыпуклая линза, радиус кривизны сферической поверхности которой = 60мм, соприкасается со стеклянной пластинкой. Оценим радиус наблюдаемой в отраженном свете интерференционной картины, если длина волны света 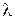= 0,60 мкм и 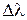=0,06 мкм. Свет падает практически нормально.

При нормальном падении света ограничивать интерференционную картину будет только длина когерентности . Кольца исчезают, когда разность хода волн становится равной длине когерентности

,

где 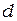— ширина зазора в месте исчезновения колец. Согласно формуле (5.2) ширина зазора , а длина когерентности из (3.3).Из этих формул получим , откуда максимальный радиус видимого кольца

=0,6 мм.

Отсюда следует, что при обычных размерах линз интерференционную картину необходимо рассматривать в микроскоп.

Максимальное число видимых колец, согласно (3.2), равно . Этот результат можно получить и из формулы (5.3).

6. ИНТЕРФЕРОМЕТРЫ И ИНТЕРФЕРОМЕТРИЯ

Интерферометрия – это оптические измерения с использованием явления интерференции. Как правило, это тонкие и точные измерения, выполняемые на специальных приборах - интерферометрах. В качестве интерферометра могут использоваться установки, собранные для наблюдения и изучения интерференции.

Условие (1.16) максимума интерференции включает длину волны излучения, показатели преломления сред, в которых распространяется излучение, и длину хода лучей, определяемую геометрическими параметрами установки. Определяя положение или смещение максимумов и минимумов интерференционной картины, можно соответственно определить:

а) длину волны излучения;

б) показатели преломления, их изменение, а также другие параметры среды, влияющие на показатель преломления, например, давление газа или состав газовой смеси;

в) малые или не малые размеры (например, можно воссоздать эталон метра), перемещения, деформации, скорости и т.д. Наиболее распространены интерферометры Майкельсона, Линника, Маха-Цендера, Фабри-Перо, Релея, Жамена. Для нестандартных измерений разрабатывают специальные интерферометрические схемы.

7. ОСНОВНОЙ ПРИНЦИП ИНТЕРФЕРЕНЦИОННЫХ СХЕМ

Интерференция характерна для волн любой природы и сравнительно просто наблюдается на опыте для волн на поверхности воды или для звуковых волн. Наблюдать же интерференцию световых волн можно лишь при определенных условиях. Рассмотренные выше примеры интерференции являются идеализированными, так при интерпретации предполагалось, что источник света является точечным и излучает монохроматические сферические или плоские волны. Поэтому эти результаты имеют ограниченную применимость, так как реальные источники света не являются таковыми.

Дело в том, что свет, испущенный обычными (не лазерными) источниками, не бывает монохроматическим. Такой свет можно рассматривать как хаотичную последовательность отдельных цугов синусоидальных волн, длительность отдельного цуга порядка 10^-8с, поэтому при наложении световых волн от разных источников фазовые соотношения между световыми колебаниями многократно изменяются случайным образом. Источники оказываются некогерентными, и достаточно устойчивой картины интерференции не возникает (сменяющие друг друга с весьма большой частотой картины интерференции в дальнейшем нас интересовать не будут, их регистрация требует специальных малоинерционных приемников). Поэтому для наблюдения интерференции с использованием немонохроматического света приходится прибегать к различным ухищрениям: применять спектральные фильтры, располагать источники таким образом, чтобы их можно было считать точечными и другим. И, тем не менее, когерентные световые волны можно получить даже от обычных источников. Общий принцип их получения таков: волну, излучаемую одним источником света, разделяют тем или иным способом на две части и затем накладывают их друг на друга подходящим способом.

Если разность хода этих волн от источника до точки наблюдения не превышает некоторые характерные длины, то случайные изменения амплитуды и фазы световых колебаний в двух волнах происходят согласованно (когерентно), и мы будем наблюдать интерференционную картину, например, систему чередующихся светлых и темных полос.

Как было показано ранее, образовавшиеся после разделения волны во всех интерференционных схемах можно представить как бы исходящими из двух точечных источников(действительных или мнимых — это не существенно).

Способы разделения волны от первичного источника на две когерентные между собой волны можно разбить на две группы: деление волнового фронта и деление амплитуды. На рис. 6.1приведены примеры нескольких интерференционных схем, широко применяемых на практике.

Схемы на рис. 6.1 а-г относятся к первой группе. Во всех схемах излучение источника S попадает на экран по двум различным путям (плечам) интерференционной схемы, отмеченным на рисунках индексами 1 и 2. В любом случае вместо первичного источника можно рассматривать два когерентных источника S1 и S2, находящихся на некотором расстоянии d. Для определения положения и формы интерференционных полос излучение можно считать монохроматическим. Наиболее важными характеристиками любой интерференционной схемы являются: угол схождения волны в точке наблюдения и угол между лучами, исходящими из источника S, которые каким-либо способом сводятся далее в точку наблюдения. Угол ­ называется апертурой интерференции.

Рис. 6.1. Некоторые интерференционные схемы, широко применяемые в оптике: а — схема Юнга, б — схема Ллойда, в — бипризма Френеля, г — билинза Бийе, д — интерферометр Майкельсона, е — звёздный интерферометр. Все лучи 1 и 2 идут от удалённого источника.