Геометрическая кристаллография
ОБЩИЕ ПОЛОЖЕНИЯ
Данные методические указания составлены в соответствии с программой практических занятий по дисциплине «Кристаллография и кристаллохимия и минералогия» для студентов обучающихся по направлению «Инженерная механика».
Практические задания по данной дисциплине проводятся с целью закрепления основных теоретических знаний, изложенных в соответствующем лекционном материале и состоят из трех разделов: геометрической кристаллографии, кристаллохимии, минералогии.
Первая часть методических указаний состоит из четырех работ, выполнение которых позволит студентам освоить важнейшие понятия, связанные с симметрией кристаллических веществ и законы, которым они подчиняются. Две работы посвящены кристаллохимии. Их выполнение даст возможность изучить закономерности внутреннего строения кристаллических веществ и взаимосвязь структуры кристаллов с их свойствами и внешней формой.
При проведении практического занятия по минералогии студенты познакомятся с методами выращивания монокристаллов.
Все практические занятия трех разделов тесно связанны между собой и выполняются в строгой последовательности.
Общие указания
Для выполнения работы необходимо использовать «Учебные задания» к практическим работам, модели кристаллических решеток и многогранников.
Перед выполнением работы следует внимательно ознакомиться с теоретическими основами, приведенными в начале работы, кратко изложить их и выполнить необходимые рисунки.
Для выполнения работы необходимо иметь линейку, набор цветных фломастеров, простые карандаши и тетрадь в клетку.
Результаты оформления работы следует представить в соответствии с образцом, приведенным в конце каждого задания.
Проводя работу по минералогии, необходимо соблюдать правила техники безопасности при работе с химическим оборудованием и реактивами.
ГЕОМЕТРИЧЕСКАЯ КРИСТАЛЛОГРАФИЯ
ПРАКТИЧЕСКАЯ РАБОТА №1
ПРАКТИЧЕСКАЯ РАБОТА №2
ПРАКТИЧЕСКАЯ РАБОТА №З
ВЫБОР КРИСТАЛЛОГРАФИЧЕСКИХ ОСЕЙ
И УСТАНОВКА КРИСТАЛЛОВ.
СИМВОЛЫ ГРАНЕЙ
Трехмерная система координат в кристаллографии выбирается соответственно симметрии кристалла. В общем случае - это косоугольные координаты с разными масштабными отрезками по осям, которые дают возможность описать любую грань тремя простыми целыми числами.
В кристаллографии используется правая система координат. Оси координат выбираются по осям симметрии или по нормалям к плоскостям симметрии, а если их нет - по ребрам кристаллического многогранника.
Для каждой сингонии являются установленные правила выбора кристаллографических осей (рис.7).
Отрезок, который отсекается гранью по оси Х обозначается а, по оси Y - b , по оси Z - с. Угол между осями Z и Y - a, между Х и Z - b, между Х и Y - g.
Каждую сингонию можно характеризовать элементарным параллелепипедом с сторонами а,b,с и углами между нимиa, b, g.
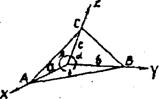
Рис.7 Геометрические константы кристалла.
В триклинной сингонии оси координат выбирают по трем непараллельным одного другому ребрам кристалла, при этом ось Z-вдоль наибольшего ребра кристалла, с>а>b. Углы между кристаллографическими осями должны по возможности приближаться к прямым (b< 90° ).
Элементарный параллелепипед косоугольный.
В моноклинной сингонии ось Y выбирается вдоль оси L2, нормально к плоскости Р, Х и Z - к плоскости, перпендикулярной к Y. Углы между кристаллографическими осями: a=g=90°; b>90. Элементарная ячейка - прямая призма с параллелограммом в основе.
В ромбической сингонии система координат прямоугольная. Оси координат выбираются вдоль L2 или по нормали к Р. Обязательным условием является: с>а>b; a=b=g=900. В случае L2 2Г ось Z выбирается вдоль L2, Х и Y - по нормалям к Р Элементарная ячейка – параллелепипед.
В тетрагональной сингонии ось Z выбирается вдоль L4, оси Х и Y - вдоль L2 или нормально к Р в плоскости, перпендикулярной Z. Отрезки по Х и Y одинаковые. Элементарная ячейка - призма с квадратом в основе.
В кубической сингонии оси координат выбираются вдоль осей L4, а если их нет – вдоль L2.
Элементарный параллелепипед - куб.
Формы элементарных параллелепипедов всех сингонии показаны на рис. 8.
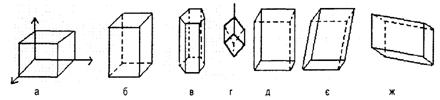
Рис.8 - Элементарные параллелепипеды разных сингоний:
а - кубическая; б - тетрагональная; в - гексагональная; г - тригональная; д - ромбическая; с - моноклинная; ж - триклинная
Для тригональной и гексагональной сингоний более удобным является введение дополнительной координатной оси Y.
Здесь ось Z выбирается вдоль L3 или L6. В плоскости, перпендикулярной к оси Z, располагаются три координатные оси X, Y и Y’ (по L2 или нормалям к Р), углы между этими осями составляют 120° Элементарная ячейка в гексагональной сингонии - прямоугольная призма с ромбом в основе Три таких ячейки составляют гексагональную призму. В тригональной сингонии элементарная ячейка - ромбоэдр (сжатый или растянутый вдоль одной из пространственных диагоналей куб) а=b=с, a=b=g¹90 0.
Кристаллографические системы координат всех сингоний изображены на рис. 9.
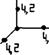
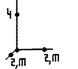
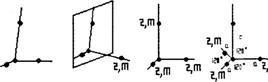
Рис. 9. Кристаллографические системы координат разных сингоний
Кристаллографические системы координат дают возможность охарактеризовать взаимное расположение граней. Для этого некоторую грань, которая пересекает все три оси, принимают за единичную (масштабную). Отрезки, которые отсекаются этой гранью на осях, является единицей или масштабом для данных осей.
Пусть задана некоторая грань АВС и масштабная грань А1 В1 С1.
Тогда 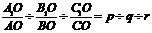
Однако в кристаллографии для числовой характеристики грани применяются не числа p, q, r, а обратные им величины. Сведя к общему знаменателю и отбросив его, получаем три целых числа h, k, l, названные символами граней (индексами Миллера). Символы граней записываются в круглых скобках без знаков препинания между ними (рис.10): 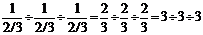 .
.
Символ грани АВС – (ЗЗЗ). Для простоты будем применять только индексы (111), независимо от расположения грани относительно единичной. Если грань параллельная к какой-нибудь кристаллографической оси, то ее символ по этой оси превратится в 0, потому что число, разделенное на ∞ дает 0. Например, грань параллельная оси X, будет иметь символ (011), параллельная оси Y – (101), параллельная оси Z – (110) Если грань пересекает ось в отдаленной части, то над соответствующим символом ставится знак "-".
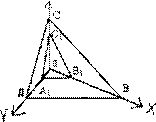
Рис.10. Символы граней
| и В | \ |
На рис. 11 приведены символы граней куба. Передняя и задняя грани имеют символы 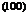 и(
и( 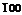 ), боковые
), боковые 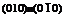 , верхняя и нижняя
, верхняя и нижняя 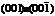 .
.
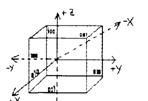
Рис.11. Символы граней куба
Особое внимание следует уделить символам граней тригональных и гексагональных кристаллов. Здесь будет не три, а четыре цифры. Следует учитывать, что дополнительное значение оси Y’ будет в области, направленной от нас, а отрицательное - к нам (рис.12). Грани гексагональной призмы в четырехосной системе координат будут иметь символы 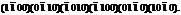
Из приведенных примеров видно, что однотипные грани имеют похожие символы. Так, символ куба можно представить как (100), а символ боковых граней гексагональной призмы - {1100}
Порядок выполнения работы:
1. Внимательно изучить полученные модели многогранников (заданные рисунки);
2. Определить элементы и формулу симметрии;
3. Определить сингонию и класс симметрии;
5. Соответственно правилам данной сингонии выбрать кристаллографическую систему координат;
6. Определить число однотипных граней;
7. Для каждого сорта граней определить их символы, записав их в столбик.
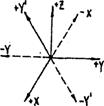
Рис. 12 - Направление осей в гексагональной и тригональной сингониях.
Пример. Модель в виде тетрагональной призмы (рис. 13):
1. Формула симметрии L44L25РС,
2. Сингония - тетрагональная, класс планаксиальний;
3. В соответствии с правилом установки кристалла ось Z выбираем вдоль L4, а оси Х и Y - по осям L2 так, чтобы они проходили через центр граней;
4. В модели есть две разновидности граней - четыре боковых грани, верхняя и нижняя грани;
5. Символы граней: 4 2
(100) (011)
(100) 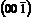
(010) 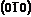
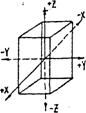
Рис. 13 - Тетрагональная призма
ПРАКТИЧЕСКАЯ РАБОТА №4
ПРАКТИЧЕСКАЯ РАБОТА №5
КРИСТАЛЛИЧЕСКАЯ РЕШЕТКА
Кристаллической решеткой называется бесконечное векториальное построение, в котором атомы или ионы занимают определенное геометрическое положение. Кристаллическая решетка строится на трех основных не компланарных трансляциях, параметрах решетки а, в, с. Кристаллические решетки характеризуются элементарным параллелепипедом - наименьшим объемом, выражая закономерность расположения атомов или ионов в пространстве.
Элементарный параллелепипед должен отвечать следующим условиям:
1. Симметрия всей кристаллической решетки должна быть одинаковой;
2. Число прямых или равных углов и равных ребер должно быть максимальным;
3. Элементарная ячейка должна иметь минимальный объем.
Иногда удобно выбирать элементарную ячейку в которой, кроме узлов в вершинах, имеются и другие узлы. Для примера рассмотрим как лучше выбрать плоскую элементарную решетку в плоской сетке, изображенной на рис. 22.
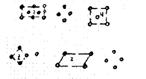
Рис. 22 - Выбор элементарной ячейки
Ячейка 3 наименьшая по площади, но не отвечает симметрии решетки; ячейка 2 отвечает симметрии, но у нее нет прямых углов; ячейка 1 отвечает симметрии, углы у нее прямые, но она не отвечает условию минимума площади. Только ячейка 4 целиком характеризует данную плоскую сетку.
Еще в середине XIX столетия, когда микроструктура веществ была неизвестна, Бравэ, исходя из идеи о периодическом размещении центров тяжести сферических частиц, показал, что все многообразие кристаллических структур можно описать с помощью 14 типов решеток, которые подразделяются на 7 кристаллографических сингоний. По расположению узлов решетки разбиваются на четыре типа: примитивные (Р), в которых узлы решеток располагаются только в вершинах; объемноцентрированные (J) - имеют дополнительный узел в центре решетки; гранецентрированные (F) - дополнительные узлы по одному в центре каждой грани; базоцентрированные (С, А, B) - дополнительные узлы в центре двух противоположных граней (рис. 23).
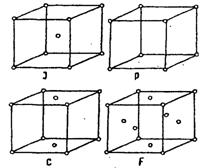
Рис. 23. Примитивная (Р), объемноцентрированная (J),
гранецентриррованная (F) и базоцентрированная (С) решетки
Только в ромбической сингонии есть все четыре типа элементарных параллелепипедов. В тригональной, гексагональной и триклинной - только примитивные; в моноклинной - примитивная и базоцентрованная; в кубической - примитивная, объемноцентрированная и гранецентрированная, в тетрагональной - примитивная и объемноцентрированная (табл.5). Следует помнить, что кристаллические решетки имеют бесконечное строение, поэтому узел, который находится в вершине кристаллических решеток, принадлежит одновременно восьми элементарным ячейкам, и на одну ячейку приходится 1/8 узла (атома, иона, группы, табл.5). Итак, на одну примитивную ячейку приходится 1/8 х 8=1 (атом).
На одну объемноцентрированную решетки приходится 1/8х8+1=2 (атома); на одну гранецентрированную решетку - 1/8х8+1 2х6 = 4 (атома); на одну базоцентрированную решетку - 1/8х 8+1/2х2 = 2 (атома).
Ребра элементарных ячеек принимаются за кристаллографические оси. Трансляция по Х обозначается а, по Y - в, по Z – с.
Трансляция обязательно берется между двумя одинаковыми узлами. Так, например, в решетках NaCl чередуются атомы Nа и Сl. Однако элементарная трансляция будет равняться расстоянию Nа - Cl ли Сl-Сl. Один из узлов кристаллических решеток принимаем за начало системы координат (рис. 24). Координаты этого узла будут [000], координаты узлов на вершинах объємноцентрированной решетки:
[111], [101], [011], [101], [001], [110], [100], а координаты узла, который находится в центре решетки, - 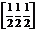 .
.
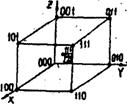
Рис. 24. Координаты узлов объємноцентрированной решетки
Таблица 5
Тип решеток Бравэ
| Сингония | Тип решетки | |||
| Примитивная | Базоцентрированная | Объемноцентрированная | Гранецинтрированная | |
| Триклинная |  Р Р | |||
| Моноклинная |  Р Р | 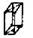 | ||
| Ромбическая | 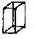 С С | 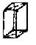 С С | 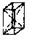 I I | 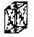 F F |
| Тригональная |  Р Р | |||
| Тетрагональная | 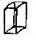 P P |  I I | ||
| Гексогональная |  P P | 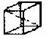 I I | 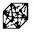 F F | |
| Кубическая | 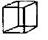 P P |
Для определения плоскостей, которые можно провести в элементарных ячейках пространственных решеток (следовательно, и в самих пространственных решетках), а также для определения кристаллографических направлений в кристаллографии принята система индексации. По этой системе для кубической решетки индексация плоскостей осуществляется тремя цифрами, заключенными в круглые скобки. Эти цифры представляют собой три взаимно простых целых числа, пропорциональных обратной величине отрезков, отсекаемых плоскостью на координатных осях, причем за единицу измерения отрезков принимают параметр решетки. На рис. 25 даны обозначения некоторых плоскостей кубической элементарной ячейки.
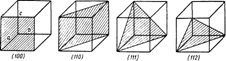
Рис. 25 Индексация плоскостей в кубической решетке
В гексагональной элементарной ячейке индексацию плоскостей производят по обратным величинам отрезков, отсекаемых рассматриваемой плоскостью на четырех кристаллографических осях (рис. 26), три из которых а1,а2 и а3 лежат в плоскости основания шестигранной призмы (в так называемой плоскости базиса), а четвертая с совпадает с осью призмы. На рис. 26 указаны также обозначения некоторых плоскостей в гексагональной ячейке. Знак минус над цифрой показывает, что плоскость отсекает отрезок на отрицательном направлении оси. Заметим, что обозначение отдельных плоскостей в элементарных ячейках кристаллографической решетки сохраняют одинаковым для всех плоскостей, проведенных в пространственной решетке, параллельных данной рассматриваемой плоскости.
В пространственной решетке рассматривают также кристаллографические направления. В качестве прямой, определяющей направление какого-либо семейства параллельных прямых, обычно выбирают прямую, проходящую через начало координат. Вдоль этой прямой расположен ряд атомов, отстоящих один от другого на определенном. расстоянии. Положение этой прямой в пространстве определится координатами любого атома, на ней расположенного. Поэтому в. качестве индексов направления берут три взаимно простых целых числа, пропорциональных координатам любого атома, лежащего на рассматриваемой прямой, причем за единицу измерения принимается параметр решетки (индексы направлений заключаются в квадратные скобки). На рис. 27 дано схематическое изображение основных направлений в кубической элементарной ячейке и их обозначение.
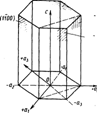
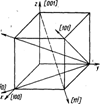
Рис. 26 Индексация плоскостей Рис. 27 Индексация направлений
в гексагональной решетке в кубической решетке
Порядок выполнения работы:
1. Внимательно изучить полученные типы кристаллических решеток;
2. Выделить элементарную ячейку в кристаллической решетки;
3. Определить тип решетки Бравэ;
4. Определить координаты узлов;
5. Определить количество атомов каждого рода, которые приходятся на элементарную ячейку, вычислить число формульных единиц, которые входят в ячейку.
КРИСТАЛЛОХИМИЯ
ПРАКТИЧЕСКАЯ РАБОТА №6
И ПЛОТНОСТИ УПАКОВОК
Координационным числом (к.ч.) данного атома или иона называется число ближайших однотипных соседних атомов или ионов в кристаллической структуре. Если центры ближайших атомов соединить прямыми линиями, получается координационный многогранник. Атом, для которого строится координационный многогранник, находится в его центре.
Ионные структуры являются устойчивыми, если каждый ион окружен ионами. На основе геометрической схемы можно рассчитать границы стойкости структур. Такой расчет дает следующие границы стойкости (А - катион, Х –анион):
Координационное число Координационный многогранник
0...0,15 2 Гантель
0,15... 0,22 3 Треугольник
0,22... 0,41 4 Тетраэдр
0,41... 0,73 6 Октаэдр
0,73... 1,00 8 Куб
1,00 12 Кубооктаэдр
Для ковалентных структур координационное число определяется из формулы (8 – N), N- номер группы периодической системы, где находиться элемент. Так, например, сера находиться в 6 группе, ее координационное число будет 8-6=2, если отношение ra/rx находится вблизи пограничного, ион может иметь два координационных числа. Координационное число зависит не только от геометрических размеров, но и от поляризуемости атомов, от характеров сил связи.
Для устойчивости кристаллических решеток необходим минимум потенциальной энергии. Одним из факторов, уменьшающим потенциальную энергию, является максимальное сближение структурных единиц, их плотная упаковка. Тенденция к плотной упаковке является характерной для всех кристаллических структур, но сильнее всего она выражена в ионных и металлических структурах.
Если условно представить себе, что атомы являются сферическими шарами, то в плоскости шары укладываются плотно следующим образом: каждый шар окружен 6-ю шарами и 6-ю лунками, а каждая лунка тремя шарами. Второй слой шаров укладывается, закрывая половину лунок. Между двумя слоями шаров образуется два типа пустого пространства, которые отличаются по координационному окружению.
Пустоты первого типа образуются тремя шарами и находятся над вторым слоем шаров. Такая пустота называется тетраэдрической, потому что центры четырех шаров образуют правильный тетраэдр (рис. 28 а).
Пустоты второго слоя находятся над пустотами первого слоя: пустота окружена 6-ю шарами располагающимися по вершинам октаэдра. Соответственно, пустоту называют октаэдрической (рис. 28 б).
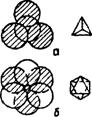
Рис. 28 – Пустоты плотной упаковки: а – тетраэдрическая,
б – октаэдрическая
Третий слой упаковки можно представить двумя способами. Первый способ - это расположение шаров таким образом, чтобы центры шаров первого слоя находились над центрами второго слоя. При этом образуется упаковка типа АВАВ. Она называется гексагональной плотной упаковкой (ГПУ) (рис. 29а). Такая упаковка имеет ось симметрии третьего порядка. ГПУ характерна для Мg, Ве, Zn и некоторых других металлов. Если поместить шары третьего слоя в другие лунки, то не третий слой повторит первый, а лишь четвертый. Выходят упаковки типа АВС. Такая упаковка имеет четыре оси симметрии L3. Она называется кубической и отвечает гранецентрованной кубической решетке (ГЦК) (рис. 29б). По этому типу кристаллизуются такие металлы, как Сu, Аu, Аg , Рt, Са, Sr, Рb и др.
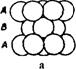
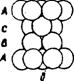
Рис. 29 – Плотные упаковки: а - двухслойная гексагональнальная типа АВАВ, б – трехслойная кубическая типа АВС
Порядок выполнения работы:
1. Внимательно изучить полученные кристаллические решетки
2. Определить к.ч. для всех атомов, которые входят в заданную структуру;
3. Определить тип координационных многогранников
4. Вычислить к.ч. атомов с учетом ионных радиусов и границ устойчивости.
5. Определить тип упаковки
6. Найти тетраэдрические и октаэдрические пустоты в упаковке.
МИНЕРАЛОГИЯ
Практическая работа №7
ВЫРАЩИВАНИЕ КРИСТАЛЛОВ
Из существующих методов выращивания кристаллов наиболее распространенными являются кристаллизация из пересыщеных растворов и расплавов солей.
Образование кристаллов из жидкой фазы (раствора или расплава) зависит от механизма и условий протекания процесса кристаллизации. Обычно различают два механизма: гомогенный, когда новая фаза зарождена в объеме старой, и гетерогенный, когда этот процесс наблюдается на границе фаз.
Начальной стадии кристаллизации является образование критического зародыша. Зародыши, радиус которых меньше 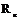 , метастабильны и растворяются (расплавляются) вновь, потому что их увеличение связанно с повышением свободной энергии. Зародыши, имеющие размер выше критического, напротив, устойчивы и способны расти, т.к. величина
, метастабильны и растворяются (расплавляются) вновь, потому что их увеличение связанно с повышением свободной энергии. Зародыши, имеющие размер выше критического, напротив, устойчивы и способны расти, т.к. величина 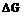 понижается. Такие зародыши называются центрами кристаллизации.
понижается. Такие зародыши называются центрами кристаллизации.
Размер критического зародыша будет равен 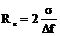 , где
, где
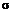 - коэффициент поверхностного натяжения между твердой и жидкой фазами;
- коэффициент поверхностного натяжения между твердой и жидкой фазами;
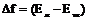 , где
, где 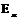 и
и 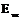 - свободная энергия единицы объема жидкой и твердой фаз.
- свободная энергия единицы объема жидкой и твердой фаз.
Дальнейший рост зародыша происходит в результате перехода атомов из переохлажденной жидкости (расплава) к кристаллам.
Кристалл растет послойно, при этом каждый слой имеет одноатомную толщину.
Различают два элементарных процесса роста кристаллов.
1. Флуктуационное образование двумерного зародыша одноатомной толщины на плоских гранях кристалла. Двумерный зародыш должен иметь размер не меньше критического. При меньшем размере зародыш не будет устойчив, т.к. вследствие образование дополнительной поверхности раздела свободная энергия системы возрастает.
2. Рост двумерного зародыша за счет атомов, поступающих из переохлажденной жидкости (расплава). После образования на плоской грани двумерного зародыша дальнейший рост нового слоя протекает сравнительно легко, т.к. появляются участки, удобные для закрепления атомов, переходящих из жидкости. Скорость роста кристаллов определяется вероятностью образования двумерного зародыша. Чем больше степень переохлаждения, тем меньше величина зародыша, и тем легче он образуется.
Процесс выращивания кристаллов из пересыщенных растворов заключается в приготовлении последнего. Существует различные методы создания пересыщенного состояния растворов: испарение растворителя, высаливание растворенного вещества, химического взаимодействия веществ, термический метод.
Термический метод является наиболее распространенным и используется для веществ с большим положительным и отрицательным температурным коэффициентам растворимости. При непрерывном нагреве (или охлаждении) насыщенного раствора пересыщение монотонно возрастает. Скорость зарождения центров кристаллизации является функцией времени, пересыщения, температуры раствора и скорости его охлаждения 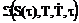 .
.
Среди способов кристаллизации из расплава особое место занимают те, в которых боковая поверхность кристалла формируется без контакта со стенками тигля – это способы Чохральского, Степанова, Вернейля. Во всех способах форма и размер получающегося кристалла определяются капиллярными силами, формирующими мениск в зоне межфазной границы и условиями тепло – и массообмена в системе кристалл-расплав.
Выращивание кристаллов способом Чохральского осуществляется со свободной поверхности расплава на затравку, поднимаемую вертикально вверх. Способ Степанова от способа Чохральского отличается наличием формообразующего устройства на поверхности расплава. По методу Вернейля тонко измельченный порошок материала, из которого выращивается кристалл, подается в пламя горелки. Порошок полностью или частично плавится, создавая на поверхности затравочного кристалла расплавленный слой. Рост кристалла происходит при последовательной кристаллизации расплава в результате опускания кристалла в более холодную зону.
Порядок выполнения работы.
I. Кристаллизация из пересыщенных растворов.
1. Взвесить исходное вещество ( 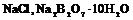 ), в количестве, превышающем его растворимость при данной температуре и растворить в 100г горячей воды.
), в количестве, превышающем его растворимость при данной температуре и растворить в 100г горячей воды.
2. Нагреть раствор на песчаной бане до полного растворения соли и отфильтровать.
3. Подвесить затравку (кристаллик на кончике шелковой нити) и опустить ее в стакан с пересыщенным раствором.
4. Аккуратно поставить содержимое стакана в эксикатор с заполненным на дне 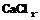
5. Внимательно изучить структуру выращенного кристалла под микроскопом, зарисовать его и указать сингонию.
II. Кристаллизация из расплавов.
1. Взять небольшое количество вещества с низкой температурой плавления ( 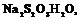
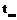 -132,7
-132,7 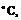 тимол,
тимол, 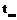 -51,5
-51,5 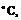 салол,
салол, 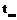 -42
-42 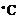 ).
).
2. Поместить исходное вещество на предметное вещество и медленным нагреванием расплавить его.
3. Полученный расплав закрыть стеклянной крышкой так, чтобы часть расплава выступала из под нее.
4. Охладить расплав до комнатной температуры и внести затравку в выступающую часть (кристаллик на кончике иглы).
5. Изучить под микроскопом характер образовавшихся кристаллов и зарисовать их.
Приложение №1
Простые формы и их комбинации в геометрической кристаллографии.
| Сингония | Виды Симметрии | Названия простых форм, возможных в данном виде симметрии | Примеры комбинаций |
| Триклинная | 1. Примитивный (моноэдрический) | Моноэдры | Кислый правый виннокислый стронций - 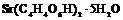 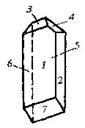 |
| 2. Центральный (пинакоидальный) | Пинакоиды | Аксинит - 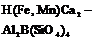 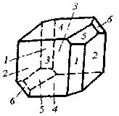 | |
| Моноклинная | 3. Планальный (диэдрический безосный) | Моноэдры Пинакоид Диэдры | Паратолуидо-изомаслянокислый эфир - 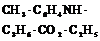 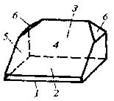 |
| 4. Аксиальный (диэдрический осевой) | Моноэдры Пинакоиды Диэдры | Молочный сахар - 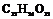 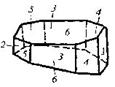 | |
| 5. Планаксиальный (призматический) | Пинакоиды Ромбические Призмы | Реальгар - 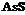 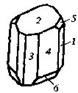 | |
| Ромбическая | 6. Планальный (ромбо-пирами-дальный) | Моноэдры Пинакоиды Диэдры Ромбические призмы Ромбические пирамиды | Струвит - 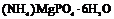 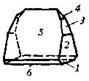 |
| 7. Аксиальный (ромбо-тетра-эдрический) | Пинакоиды Ромбические призмы Ромбические тетраэдры | Эпсомит - 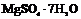 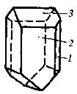 | |
| 8. Планаксиальный (ромбо-дипирамидальний) | Пинакоиды Ромбические призмы Ромбические дипирамиды | Оливин - 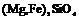 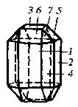 | |
| Тригональная | 9. Примитивный (тригонально-пирамидальный) | Моноэдры Тригональные призмы Тригональные пирамиды | Метапериодат натрия – гексагидрат 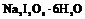 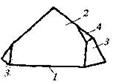 |
| 10. Центральный (ромбоэдрический) | Пинакоид Гексагональные призмы Ромбоэдры | Диоптаз - 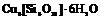 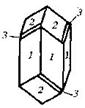 | |
| 11. Планальный (дитригонально-пирами- пальный) | Моноэдры Тригональные призмы Дитригональные призмы Гексагональная призма Тригональные пирамиды Гексагональные пирамиды Дитригональные пирамиды | Турмалин – сложный алюмосиликат, содержащий бор 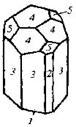 | |
| 12. Аксиальный (тригонально-трапецо-эдрический) | Пинакоид Тригональные призмы Дитригональные призмы Гексагональная призма Тригональные дипирамиды Ромбоэдры Тригональиые Трапецоэдры | Низкотемпературный кварц - 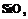 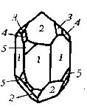 | |
| 13. Планаксиальный (тригонально-скалено-эдрический) | Пинакоид Гексагональные призмы Дигексагональны Гексагональные дипирамиды Ромбоэдры Тригональные Скаленоэдры | Кальцит - 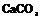 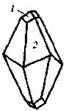 | |
| Тетрагональная | 14. Примитивный (тетрагонально-пирамидальный) | Моноэдры Тетрагональные призмы Тетрагональные пирамиды | Фергусонит - 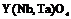 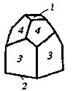 |
| 15. Центральный (тетрагонально-дипирамидальный) | Пинакоид Теграгоиальные призмы Тетрагональные дипирамиды | Повеллит - 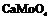 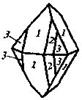 | |
| 16. Планальный (дитетрагонально-пирамидальный) | Моноэдры Тетрагональные призмы Дитетрагональные призмы Тетрагональные пирамиды Дитетрагональные пирамиды | Моногидрат фтористого серебра - 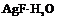 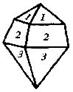 | |
| 17. Аксиальный (тетрагонально-трапецоэдрический) | Пинакоид Тетрагональные призмы Дитетрагональные призмы Тетрагональные дипирамиды Тетрагональные трапецоэдры | Дитрихлордиацетат калия - 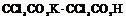 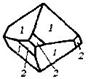 | |
| 18. Планаксиальный (дитетрагонально-дипирамидальный) | Пинакоид Тетрагональные призмы Дитетрагональные призмы Тетрагональные дипирамиды Дитетрагональные дипирамиды | Циркон -  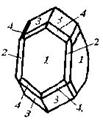 | |
| 19.Инверсионно-примитивный (тетрагонально-тетраэдрический) | Пинакоид Тетрагональные призмы Тетрагональные тетраэды | Иодид тетраэтил-аммония - 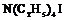 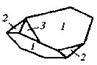 | |
| 20. Инверсионно-планальный (тетрагонально-скалено-эдрический) | Пинакоид Тетрагональные призмы Дитетрагональные призмы Тетрагональные тетраэды Тетрагональные скаленоэдры | Карбамид - 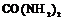 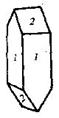 | |
| Гексагональная | 21. Примитивный (гексагонально-пирамидальный) | Моноэдры Гексагональные призмы Гексагональные пирамиды | Сульфат лития и калия - 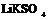 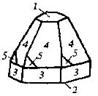 |
| 22. Центральный (гексагонально-дипирамидальный) | Пиканоид Гексагональные призмы Гексагональные дипирамиды | Апатит - 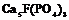 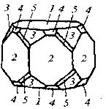 | |
| 23. Планальный (дигексагонально-пирамидальный) | Моноэдры Гексагональные призмы Дигексагональные призмы Гексагональные пирамиды Дигексагональные пирамиды | Гринокит - 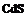 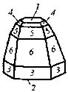 | |
| 24. Аксиальный (гексагонально-трапецоэдрический) | Пинакоид Гексагональные призмы Дигексагональные призмы Гексагональные дипирамиды Гексагональные трапецоэдры | Высокотемпературный кварц - 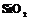 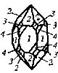 | |
| 25. Планаксиальный (дигексагонально-дипирамидальный) | Пинакоид Гексагональные призмы Дигексагональные призмы Гексагональные дипирамиды Дигексагональные дипирамиды | Берилл - 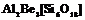 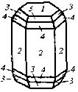 | |
| 26. Инверсионно-примитивный (тригонально-дипирамидальный) | Пинакоид Тригональные призмы Тригональные дипирамиды | Кислый фосфат серебра (?) - 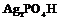 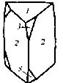 | |
| 27. Инверсионно-планальный (дитригонально-дипирамидальный) | Пинакоид Тригональные призмы Дитригональные призмы Гексагональная призма Тригональные дипирамиды Гексагональные дипирамиды Дитригональные дипирамиды | Ферросилиций - 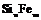 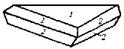 | |
| Кубическая | 28. Примитивный (пентагон-тритетра-эдрический) | Гексаэдр (куб) Ромбо-додекаэдр Пентагон-додекаэдры Тетраэдры Тригон-тритетраэдры Тетрагон-тритет-раэдры Пентагон-тритетраэдры | Хлорноватокислый натрий - 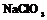 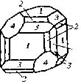 |
| 29. Центральный (гидодека-эдрический) | Гексаэдр (куб) Ромбо-додекаэдр Пентагон-додекаэдры Октаэдр Тетрагон-триокта-эдры Тригон-триокта-эдры Дидодекаэдры | Пирит - 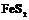 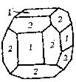 | |
| 30. Планальный (гексатетра-эдрический) | Гексаэдр (куб) Ромбо-додекаэдр Тетрагексаэдры Тетраэдры Тригон-тритетра-эдры Тетрагон-тритетраэдры Гексатетраэдры | <
