Взаимное расположение политропных
процессов в р, u –и T, S – диаграммах
Определенный интерес для осмысления частных случаев политропных процессов представляет собой их взаимное расположение в р, u –
и T, S – диаграммах.В некоторых случаях оно без подробного анализа политропного процесса позволяет дать произвольному политропному процессу достаточно объективную термодинамическую характеристику с указанием его параметров – показателя политропы.
|
Покажем это. Выберем на плоскости 
и 
– диаграмм произвольную точку, соответствующую некоторому термодинамическому состоянию системы (рисунок 5.11 и 5.12).
Проведем изохору в направлении повышения давления и также в направлении его понижения. Известно, что дифференциальное уравнение изохоры может быть записано в виде 
. Следовательно отклонение любого процесса от вертикали (изохоры) будет идти с увеличением объема ( 
> 
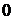) вправо от изохоры или с уменьшением объема ( < 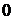), если процесс расположен влево от изохоры. Таким образом изохора как бы разбивает плоскость расположения политропных процессов на две полуплоскости, одна из которых – правая содержит процессы, протекающие с расширением системы ( > 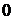), а другая – процессы с уменьшением объема системы ( < 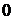), т.е. ее сжатием.
Аналогичные рассуждения могут быть проведены и относительно изобарного процесса. Если провести через состояние один горизонталь – изобару, то она так же разделит плоскость возможных политропных процессов на две полуплоскости. Процессы расположенные выше изобары идут с увеличением давления 
, ниже – с понижением 
. Дифференциальное уравнение самой изобары имеет вид 
Изотерма 
в – диаграмме, дифференциальное уравнение которой может быть записано в виде 
, разбивает плоскость возможных политропных процессов на две полуплоскости. В одной из них, расположенной левей и ниже изотермы внутренняя энергия уменьшается 
, а температура падает 
. В другой, расположенной правее и выше изотермы внутренняя энергия увеличивается, а температура растет. Адиабатный процесс 
в – диаграмме идет круче изотермы, т.к. показатель адиабаты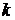 
всегда больше единицы если речь идет о термодинамических системах в газовой фазе. Дифференциальное уравнение адиабаты 
, т.к. по определению это процесс. При протекании которого система не обменивается теплом с окружающей средой. Сама кривая адиабаты разбивает плоскость адиабатных процессов на две полуплоскости. Процессы, расположенные левей и ниже адиабаты идут с отводом тепла – 
, а лежащие правей и выше адиабаты – с подводом тепла – 
.
Таким образом частные случаи политропных процессов разбивают поле возможных термодинамических политропных процессов на восемь групп 
. Процессы расположенные в одной группе образуют рядом схожих свойств.
Поясним это на примере анализа процессов, расположенных в группе 
.
Процессы этой группы расположены между адиабатой и изотермой. Следовательно их показатель политропы определяется очевидным неравенством 
. Т.к. процесс расположен ниже изотермы, то его внутренняя энергия уменьшается, а температура падает: 
, . В то же время процессы этой группы расположены правее и выше адиабаты следовательно тепло при протекании процесса будет подводиться к системе . Поскольку знак у бесконечно малого изменения количества положительный , а у дифференциала температуры – отрицательный, то теплоемкость 
будет тоже отрицательной, т.е. 
. Процессы, расположенные в третьей группе, имеют отрицательную теплоемкость.
Внутренняя энергия системы падает 
хотя тепло подводиться к системе . Это объясняется тем, что процесс расширения системы протекает столь интенсивно, что подводимого тепла недостаточно для компенсации энергетических затрат и недостающая энергия для компенсации затрат отводится от внутренней энергии самой системы.
Похожая энергетическая компенсация имеет место и в процессе расположенных в группе 
, теплоемкость которых тоже отрицательна. Несмотря на то, что теплота в процессах этой группы отводится, процесс сжатия столь интенсивно, что часть подводимой на сжатие работы идет на увеличение внутренней энергии системы и вновь у изменения 
тепло – 
и температуры противоположные знаки , а 
, а теплоемкость 
отрицательна.
5.4 С, п – диаграмма политропных процессов
Элементарный анализ термодинамики частных случаев политропных процессов позволят убедиться, что их теплоемкость 
и показатель политропы 
изменяются в достаточно широких пределах 
. Исходя из этого определенный интерес в термодинамическом анализе представляет С, п – диаграмма (рисунок 5.13)
 Рисунок 5.13  – диаграмма политропного процесса |
Для анализа воспользуемся полученной ранее зависимостью для расчета теплоемкости политропного процесса.
Элементарный математический анализ выражения, где и постоянные величины позволяет сделать вывод о том, что у приведенной функции 
имеется одна вертикальная 
и одна горизонтальная 
асимптоты. Как видно на рисунке теплоемкость политропных процессов отрицательна в диапазоне измерения показателя политропы 
, если речь идет о двухатомных газах, состояние которых достаточно хорошо описывается уравнением Клапейрона – Менделеева. График функции 
пересекает ось ординат в точке 
и приближается к асимптоте 
при устремлении показателя политропы к 
.
5.5 Экспериментальные методы определения
Показателя политропы
Способ
 Рисунок 5.14 Экспериментальный метод определения показателя политропы |
Пусть в системе координат р, u экспериментальным путем построен график 1-2 некоторого политропного процесса (рисунок 5.14). Для любых двух точек процесса, в том числе и для крайних справедливо равенство:
.
Прологарифмируем его 
= 
, и выразим показатель политропы
. (5.43)
Таким образом мы получим выражение, позволяющее по параметрам любых двух известных из опыта состояний 1 и 2 найти численное значение показателя политропы.
 Рисунок 5.15 Расчет показателей политропы по отношению работ |
Способ
Допустим, что нам известен график политропного процесса в р, u – диаграмме (рисунок 5.15). Площадка 1¢122¢1¢ – есть внешняя работа политропного процесса 
.
Площадь S 1¢¢122¢¢1¢¢ числено равна располагаемой работе
.
Из сравнения двух работ вытекает, что
. (5.43)
Способ
 Рисунок 5.16 К расчету показателя политропы через логарифмическое уравнение политропы |
Прологарифмируем уравнение политропы:
, 
.
После интегрирования получим линейное уравнение вида 
. Это наклонная прямая в системе координат ( 
р, u) (рисунок 5.16). Для изотермы 
и 
. Следовательно, в этой системе координат показатель политропы будет равен
(5.44)
Цикл Карно
Термодинамика цикла Карно
В опубликованном в 1824 году трактате «Размышления о движущей силе огня и о машинах способных ее реализовать» Сади Карно предложил цикл теплового двигателя, названный в последствии его именем, так как он играет чрезвычайно важную роль при развитии теоретических основ термодинамики и является идеальным циклом для любой силовой установки, преобразующей теплоту в механическую энергию, действие которой осуществляется в ограниченном источниками энергии диапазоне температуры. Известно, что цикл Карно состоит из двух изотерм и двух адиабат. Причины, побудившие брать именно эти процессы для идеального цикла, уже отмечались ранее. Очевидно, что для возможности реализации такого цикла необходимо сделать следующие предположения. Поверхности, ограничивающие рабочее тело (стенки цилиндра), должны обладать двумя противоречивыми свойствами. В один из моментов они должны быть бесконечно теплопроводными, чтобы обеспечить передачу тепла от высокотемпературного источника 
к рабочему телу энергию в форме тепла при отсутствии температурного перепада, процесс 1-2.
 Рисунок 6.1 р, u – и T, S – диаграммы цикла Карно |
Перенос энергии за счет теплопроводности описывается известной гипотезой Фурье
, (6.1)
где 
плотность теплового потока, Вт/м2; 
теплопроводность, Вт/(м2К); 
градиент температуры, К/м.
Отсутствие градиента температуры для переноса энергии в форме тепла требует выполнения очевидных равенств
.
Такое же условие должно быть выполнено и при реализации процесса 3-4 – отвод тепла к низкотемпературному источнику.
Другое, противоположное первому, условие состоит в том, что при отсутствии термического контакта с источниками тепла поверхности машины, ограничивающие рабочее тело (стенки цилиндра), должны быть адиабатными, то есть абсолютно теплоизолирующими, что возможно при равенстве нулю теплопроводности 
.
Качество тепловой машины оценивается величиной термического коэффициента полезного действия, под которым понимается отношение полезного за цикл эффекта (полученная работа 
) к затратам, понесенным для организации возможности реализации цикла – 
.
Тогда
, (6.2)
но в соответствии с первым началом термодинамики
,
откуда 
После подстановки выражения для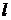 
в (6.2) придем к зависимости, справедливой для любого теплосилового цикла
. (6.3)
В полученном выражении 
и 
положительные значения тепловых эффектов в процессах отвода и подвода теплоты. Для идеального цикла – цикла Карно это тепловые эффекты в изотермических процессах 1-2 и 3-4. С учетом того, что рабочее тело – идеальный газ, они могут быть рассчитаны по зависимостям
, 
.
Тогда выражение для термического КПД цикла Карно запишем в виде следующего выражения
.
В цикле Карно адиабаты 2-3 и 4-1 протекают в пределе одного и того же интервала изменения температуры от Т1 до Т2
и 
,
следовательно,
или 
.
С учетом последнего равенства КПД цикла Карно перепишется в виде
. (6.4)
Термический КПД необратимого цикла всегда меньше КПД обратимого цикла Карно. В необратимом цикле для выполнения условия (5.35) необходимо, чтобы предельная температура рабочего тела в изотермическом процессе 1-2 была меньше температуры источника на некоторую величину DТ, а в процессе отвода тепла 3-4 она была больше температуры холодильника на DТ. Тогда уравнение для КПД необратимого цикла запишется в виде
.
После сокращения на величину 
получим
,
величина 
следовательно
,
а это означает, что справедливо неравенство
.
Вывод получен лишь для цикла Карно, у которого в качестве рабочего тела используется идеальный газ. Последнее ограничение не носит принципиального характера, но существенно упрощает анализ. Неравенство получено с учетом лишь внешней необратимости – наличие конечной разности температур в процессах теплообмена. Внутренняя необратимость: трение, механическая неравновесность, завихрения и т. д. приводят к дополнительному понижению величины полезной работы цикла 
и, следовательно, к снижению величины термического КПД 
.
 Рисунок 6.2 Обратимый цикл произвольной конфигурации |
Анализируя выражение (6.4) нетрудно сделать вывод о том, что КПД цикла Карно всегда меньше единицы. Это определено тем, что не может быть равно бесконечности 
, и не может быть равно нулю абсолютной температуры 
. Учитывая это можно отметить некоторую несостоятельность введенного параметра как КПД, так как по определению КПД должен изменяться в пределах от 0 до 1,0.
Любой обратимый цикл произвольной конфигурации можно представить как совокупность элементарных циклов Карно. При этом совокупность элементарных циклов Карно эквивалентна исходному произвольной конфигурации обратимому циклу. Адиабаты сжатия и расширения расположены столь близко друг к другу, что процессы подвода и отвода тепла могут считаться изотермическими. Так как каждая из адиабат проходится в совокупности дважды, причем один раз в прямом, а другой раз в обратном направлении, то суммарная работа цикла при его замене элементарными остается неизменной. В этом случае необходимо ввести понятие о бесконечно большом количестве источников тепла, а выше приведенные зависимости будут справедливы для каждого из элементарных циклов.
Теорема Карно
Термический КПД обратимого цикла, осуществляемого между двумя источниками тепла c различной температурой, не зависит от рода рабочего тела, при помощи которого он реализуется.
Теорема доказывается методом от противного. Пусть имеются две тепловые машины с разными рабочими телами, работа которых осуществляется между двумя источниками тепла с температурам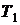и 
и 
, причем 
. термический КПД первой машины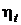 
, второй – 
. Допустим, что справедливо неравенство 
.
 Рисунок 6.3 К доказательству теоремы Карно |
Предположим, что первая машина работает по прямому, а вторая по обратному циклам. Рабочие тела по своим количествам в машинах подобраны так, что выполняется равенство
.
Очевидно, что работы, подводимая во втором и производимая в первом циклах, при этих условиях могут быть найдены по известным термическим КПД
, 
.
Так как , а , то из записанных выражений для расчета работ следует, что 
или, что тоже самое
.
Запишем выражения для термических КПД через теплоты с учетом неравенства 
:
.
Элементарный анализ неравенства с учетом равенства приводит нас к выводу
.
Следовательно, в обратном цикле от источника отбирается большее количества тепла, чем то, которое поступает в него в процессе реализации прямого цикла. Количество тепла в высокотемпературном источнике остается неизменным.
Таким образом, мы построили машину, которая отбирает от низкотемпературного источника теплоту 
и при этом производит работу 
.
Этот вывод противоречит второму закону термодинамики в формулировке Планка, что означает присутствие ошибки в исходных допущениях. Оно было единственным и состояло в том, что мы допустили зависимость КПД обратимого цикла Карно от рода рабочего тела. Следовательно КПД цикла Карно не зависит от рода рабочего тела, а для рассмотренного примера выполняем очевидное равенство
