Термические и калорические параметры состояния

Состояние рабочего тела характеризуется следующими термическими (давление, удельный объем, температура) и калорическими (внутренняя энергия, энтальпия, энтропия) параметрами.

Удельный объем 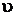– объем единицы массы, м³/кг: .

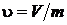Плотность – величина обратная удельному объему и представляет собой массу единицы объема, кг/м³: .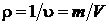

Иногда экстенсивный параметр относят к количеству вещества в системе, т. е. к числу молей:

Объем одного моля: .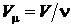

Масса равна произведению мольной массы на число молей:

,

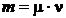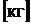
где 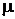– молярная масса, кг/моль; 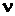– число молей.

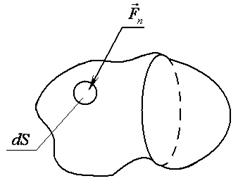Рисунок 1.2 К определению понятия давления

Давление р [Па] представляет собой отношение суммы нормальных к поверхности составляющих сил 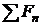, образующихся вследствие ударов о стенку микрочастиц системы в процессе их теплового хаотического движения, к площади поверхности S:

Допустим, что на элементарную площадку dS действует нормальная составляющая силы 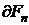, тогда давление может быть определено очевидным пределом и как математическое следствие производной нормальной составляющей силы 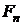на поверхности S.

.

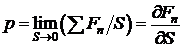Единица измерения давления – Паскаль: 1 Па = 1 Н/м².

В молекулярно-кинетической теории (МКТ) величина давления определяется основным уравнением МКТ

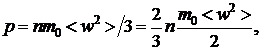(1.2)

где n – объемная концентрация молекул; и – масса и средняя квадратичная скорость молекулы соответственно.

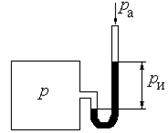Рисунок 1.3 Измерение давления жидкостным манометром

В соответствии с основным уравнением МКТ давления, оказываемое газом на стенки сосуда, численно равно 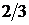кинематической энергии молекул, находящихся в единице объема. При этом надо помнить, что речь идет об энергии поступательного теплового движения газа. Ибо газ рассматривается как идеальный.

Давление подразделяется на абсолютное – р, манометрическое – 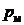, избыточное – 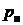и вакуум – 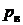. Измеренное давление всегда избыточное – 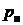. Измеряют его манометрами или вакуумметрами. Атмосферное давление измеряют барометрами – .

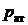Абсолютное давление равно сумме избыточного и барометрического давления, т. е. атмосферного.

.

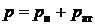Если в сосуде разрежение, то величина вакуума может быть найдена как разность атмосферного и абсолютного давлений.

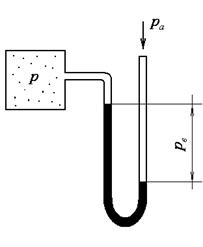Рисунок 1.4 Измерение глубины вакуумирования

.

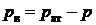В жидкостных манометрах, в зависимости от применяемой жидкости, давление измеряется в мм ртутного столба или мм водяного столба:

1мм рт. ст. = 133,32 Па, 1 мм вод. ст. = 9,8065 Па.

В термодинамике, гидравлике, механике жидкости и газа часто состояние системы сводят к нормальным физическим условиям, под которыми принято считать: температура – 273,15 К (0 °С), давление – 760 мм рт. ст. = 101325 Па.

Термодинамический процесс

Любая термодинамическая система, находящаяся в неравновесном состоянии обязательно через некоторое время переходит в равновесное состояние. Такие процессы изменения состояния принято называть самопроизвольными, а время перехода из неравновесного в равновесное состояние – временем релаксации.

Термодинамическая система, находясь в состоянии равновесия, выйти из него может лишь под воздействием со стороны окружающей среды. В этом случае через границы системы необходимо подвести либо отвести энергию. Всякий термодинамический процесс связан с изменением состояния термодинамической системы. Если в начале процесса система находилась в равновесном состоянии, то его изменение приводит к существенно неравновесным состояниям, когда температура и плотность по объему, занимаемому системой, становятся неодинаковыми. Таким образом, любое изменение состояния, строго говоря, протекает через неравновесные состояния. Такие процессы принято называть неравновесными либо нестатическими.

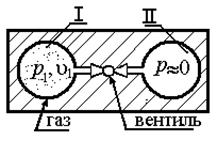Рисунок 1.5 Процесс заполнения объема

Рассмотрим изолированную систему, представленную на рисунке 1.5. Если открыть вентиль, то начнется процесс истечения из сосуда I и заполнение сосуда II.

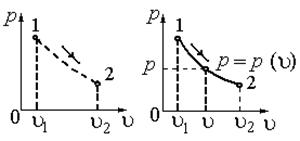а) б)   Рисунок 1.6 Представление процессов в р, u – диаграмме: а – условное изображение нестатического процесса; б – процесс квазистатического (равновесного) изменения состояния

При этом за счет отрывных явлений в потоке газа будут возникать завихрения, создающие значительную разность давления и температуры у различных областей как втекающего потока, так и во всей области, занимаемой вторым сосудом. Переход начального равновесного состояния в конечное равновесное состояние системы будет происходить через некоторую совокупность промежуточных неравновесных состояний, описание которых уравнением состояния системы невозможно. Любое уравнение состояния справедливо лишь для равновесных состояний. Следовательно, нестатический, неравновесный процесс не может быть изображен в р,u – диаграмме.

Процессы, протекающие из начального равновесного в конечное равновесное состояние через совокупность промежуточных равновесных состояний, будем называть квазистатическими или равновесными процессами изменения состояния.

Строго говоря, равновесных или статических процессов в природе существовать не может. Для их реализации необходимо, чтобы механические или термические воздействия на систему были бесконечно малы.

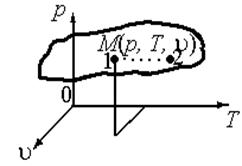Рисунок 1.7 Термодинамическое пространство

Таким образом, квазистатическое (квазиравновесное) состояние необходимо рассматривать как идеализированный предельный случай, когда система постоянно находится вблизи равновесных состояний, так что все ее состояние с достаточной степени точности можно описать общими для всей системы параметрами состояния.

Если соединить начальное, все промежуточные и конечное состояния линией, то на диаграмме получим кривую процесса изменения состояния, для каждой точки которой применимо термическое уравнение состояния.