Если разность хода равна целому числу длин волн или четному числу полуволн, то будет наблюдаться максимум интенсивности при интерференции.

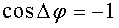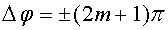Аналогично найдем условие минимума. Если , то , где m = 0, 1, 2, ...

Тогда

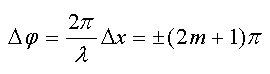
и

Условие минимума интенсивности при интерференции читается следующим образом.

Если разность хода равна нечетному числу полуволн, то в данной точке экрана будет наблюдаться минимум интенсивности при интерференции.

Расчет интерференционной картины от двух когерентных источников

Два когерентных источника можно получить, например, методом Юнга. Рассчитать интерференционную картину - это значит предсказать, в какой точке экрана наблюдения будет максимум, а в какой минимум интенсивности (рис. 3.9).

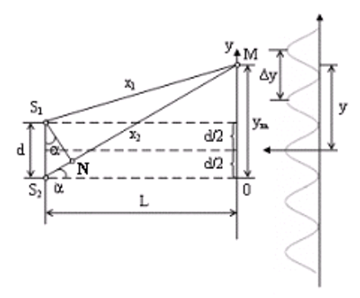
Рис. 3.9

На рис. 3.9 приняты следующие обозначения:
S₁ и S₂ - когерентные источники;
d - расстояние между когерентными источниками;
L - расстояние от источников до экрана наблюдения;
Δx- разность хода, Δx = S₂M - S₁M;
Δy - ширина интерференционной полосы;
y_m - координата темной или светлой интерференционной полосы с номером m; 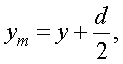где y - координата от центра картины. Учтем, чтоу_m>> 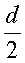, тогдау_m≈y.

Кривая с максимумами и минимумами представляет собой распределение интенсивности вдоль экрана наблюдения.

Для того чтобы рассчитать интерференционную картину, рассмотрим два подобных треугольника: .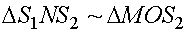

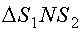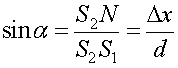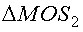Из найдем синус угла α: ; из найдем тангенс угла α .

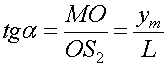Так как угол α мал, то 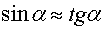и 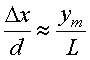. Тогда координата интерференционной полосы с номером m равна

.

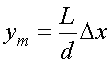Для светлых полос выполняется условие максимума. С учетом (3.37) координата светлой полосы определяется по формуле:

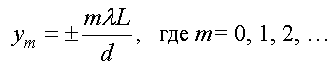
Аналогично координата темной полосы с номером m с учетом (3.38) равна:

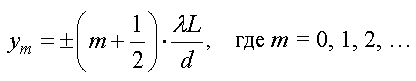
Шириной интерференционной полосы называется расстояние между соседними максимумами или расстояние между соседними минимумами (рис. 3.8):

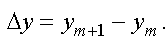
Рассчитаем ширину интерференционной полосы для светлых полос:

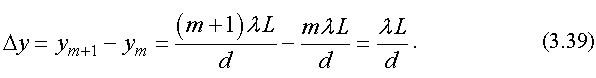
Формула 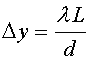(3.39) показывает, что для того, чтобы интерференционная картина была отчетливой, необходимо соблюдение условия d << L. Эту формулу можно использовать для того, чтобы определить длину волны света

Именно таким способом впервые были определены длины волн для световых лучей разного цвета.
Формула (3.40) является рабочей в лабораторной работе "Изучение интерференции света".

Оптическая разность хода

Условия максимума и минимума интенсивности при интерференции (3.37) и (3.38) справедливы, если интерферирующие лучи распространяются в вакууме (или в воздухе). Если лучи распространяются в среде (например, в воде, в стекле), то вводятся понятия "оптический путь" и "оптическая разность хода".

Оптическим путем называется произведение показателя преломления на геометрический путь

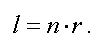
Оптической разностью хода называется разность оптических длин путей

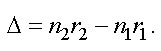
Условие максимума при интерференции тогда будет формулироваться следующим образом. Оптическая разность хода равна четному числу полуволн

А условие минимума при интерференции будет записано так: оптическая разность хода равна нечетному числу полуволн

где m - порядок (или номер) интерференционного максимума или минимума от центра интерференционной картины, m = 0, 1, 2, ...