Краткие методически указания по

Кафедра общей физики

Физика

Методические указания и контрольные задания

для студентов заочного отделения.

Ч а с т ь II

ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ

Пермь 2002

УДК 53(07):378

Б 24

План УМД 2001/2002 уч./г.

Физика: Методические указания и контрольные задания для студентов заочного отделения. Часть II. Электричество и магнетизм / Перм. гос. техн. ун-т, Пермь, 2002. - 78 с.

Составители: Щицина Ю.К., ст. преподаватель, Вотинов Г.Н., к.ф.-м.н., ст. преподаватель, Перминов А.В.,к.ф.-м.н., ст. преподаватель, Черноиванова Т.М.,ст. преподаватель, Коновалова М.А.,ассистент. Под общей редакцией Цаплина А.И., д.т.н., профессора.

Приведены общие рекомендации по применению физических зако­нов и формулы к решению задач, рабочая про­грамма, список литературы, примеры решения задач по темам "Электричество и магнетизм", тренировочные зада­чи с ответами, проверочный тест и задачи для выполнения двух контрольных работ. Даны таблицы с номерами вариантов и номерами задач для каждого варианта, а также справочные таблицы.

Рецензент: Лоскутов К.Н., к.ф.-м.н., доцент.

Издание стереотипное. Утверждено на заседании кафедры.

ã Пермский государственный

технический университет, 2002

СОДЕРЖАНИЕ

Введение............................................................................................. 4

Список литературы............................................................................ 4

1. Краткие методические указания по самостоятельному

изучению курса.................................................................................. 5

2. Методические указания к решению задач........................................ 5

3. Основные формулы. Электростатика. Электрический ток.............. 7

3.1. Примеры решения задач............................................................ 12

3.2. Тренировочные задачи............................................................... 28

3.3. Проверочный тест....................................................................... 30

3.4. Контрольная работа № 3............................................................ 32

4. Основные формулы. Электромагнетизм........................................... 42

4.1. Примеры решения задач............................................................ 45

4.2. Тренировочные задачи............................................................... 59

4.3. Проверочный тест....................................................................... 61

4.4. Контрольная работа № 4............................................................ 63

5. Вопросы для подготовки к экзамену................................................ 75

6. Справочные таблицы......................................................................... 77

ВВЕДЕНИЕ

Цель настоящего издания - снабдить студентов-заочников ра­бочей программой и контрольными заданиями по курсу общей физики.

Весь учебный материал программы курса разделен на три час­ти:

1. "Механика, молекулярная физика и термодинамика".

2. "Электростатика. Постоянный ток. Электромагнетизм".

3. "Оптика. Физика атома и атомного ядра".

Каждая из частей содержит: рабочую программу, список учебной литературы, примеры решения задач, тренировочные задачи, контрольные задания, справочные таблицы.

Распределение объемов занятий и видов учебной работы при изучении физики для студентов-заочников всех специальностей дано в табл. 1.

Таблица 1

	Занятия, часы
Семестр	Лекции	Лабора-торные работы	Практи-ческие	Самосто ятельная работа	Выпол-нение контро-льных работ	Конт-роль
1-4	8-32	8-12	–	185-456	2-6	Экзамен и/или зачет

Основной формой изучения дисциплины является самостоятельная работа студента над рекомендованной литературой. Целесообразно проработать материал, пользуясь примерами решения задач, тренировочными задачами, контрольными заданиями, справочными таблицами.

СПИСОК ЛИТЕРАТУРЫ

Основная

1. Трофимова Т.И. Курс физики: Учебное пособие.-7 изд., испр.-М.: Высш. шк, 2001.-542 с.

Дополнительная

2. Савельев И.В. Курс общей физики. М.: Наука,1988. Т.1-3.

3. Детлаф А.А., Яворский Б.М. Курс физики. М.: Высш. шк., 1989.

4. Лабораторный практикум по физике. Под ред. К.А. Барсукова и Ю.И. Уханова. М.: Высш шк., 1988.

Электростатика

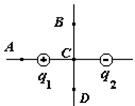1. В какой из четырех точек А, В,С.D (см. рис). некоторый положительный заряд q₃ может находиться в равновесии?

Варианты ответа:

1. В точке А. 2. В точке В. 3. В точке С. 4. В точке D.

2. Шарик массой 2,0 г, имеющий заряд 2×10^-6 Кл, подвешен в воздухе на тонкой нити. Каким будет натяжение нити, если снизу шарика на расстоянии 5 см от него расположен одноименный заряд 1,2×10^-7Кл.?

Варианты ответа:

1. 11×10^-3 Н. 2. 23×10^-3 Н. 3. 0,65×10^-2 Н. 4. 20×10^-3 Н. 5. 8,6×10^-3 Н.

3. В каких из четырех случаев распределения зарядов напряженность электростатического поля в точке А Е_А = 0 (см. рис.).

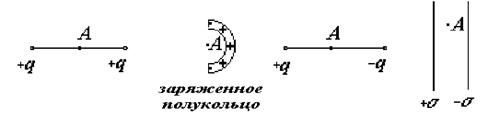
1. 2. 3. 4.

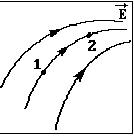
4. На рисунке приведена картина силовых линий электростатического поля. Какое соотношение для напряженностей Е и потенциалов jв точках 1 и 2 верно ?

Варианты ответа:

1) Е₁ < E₂ , j₁ > j₂;

2) Е₁ > E₂ , j₁ < j_2;

3) Е₁ > E₂ , j₁ > j_2;

4) Е₁ < E₂ , j₁ < j_2;

5) Е₁ = E₂ , j₁ < j₂ .

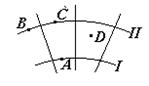5. На рис. показаны силовые линии и две эквипотенциальные поверхности I и II в электростатическом поле. Какие точки имеют одинаковые потенциалы?

Варианты ответа: В и С. 2. A и D. 3. B, C и D. 4 A, B и C. 5. A, B,C,D .

6. Плоский конденсатор между обкладками содержит диэлектрик. Конденсатор подключили к источнику напряжения, а затем удалили диэлектрик. Что при этом произошло?

А. Напряжение на обкладках уменьшилось.

Б. Емкость конденсатора уменьшилась.

В. Напряженность поля увеличилась.

Г. Заряд на обкладках уменьшился.

Варианты ответа: 1) только Б и Г; 2) только А и Б;

3) только В и Г; 4) Б, В и Г; 5) А, Б, В и Г.

7. Какие из нижеприведенных выражений дают в той или иной форме поток вектора напряженности 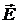через произвольную замкнутую поверхность?

Варианты ответа:

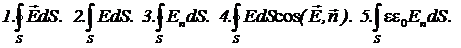
8. Какие из равенств соблюдаются 1) при последовательном соединении; 2) при параллельном соединении конденсаторов с емкостями С₁ и С₂?

Варианты ответа:

1. С = С₁ + С_2. 2. 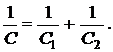3. q =q₁= q₂. 4. q = q₁+ q_2.

5. U = U₁ + U₂, 6. U = U₁ + U₂.

9. На заряд q, помещенный между пластинами плоского воздушного конденсатора емкостью С и площадью каждой пластины S, действует сила F. Какова энергия конденсатора?

Варианты ответа:

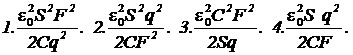
Постоянный ток

1. В проводнике длиной l и площадью поперечного сечения S течет постоянный электрический ток. Средняя скорость направленного движения носителей тока v, их количество в единице объема n, а заряд частицы q. Какое из выражений дает силу тока в проводнике?

Варианты ответа: qvnS. 2. qvn. 3. qvnS/l. 4. qvnS. 5. qvnl/S.

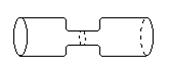
2. Ток идет по проводнику, форма которого показана на рис. Одинакова ли напряженность поля в местах с узким и широким сечениями?

Варианты ответа:

1. Не одинакова. 2. При постоянном токе - одинакова, при переменном - разная. 3. При переменном токе - одинаковая, при постоянном - разная. 4. Одинакова.

3. Источник тока, амперметр и некоторое сопротивление соединены последовательно в замкнутую цепь. Сопротивление сделано из медной проволоки длиной 100 м и поперечным сечением 2 мм². Сопротивление амперметра равно 0,05 Ом. Амперметр показывает 1,43 А. Определить э.д.с. источника, если его внутреннее сопротивление 0,5 Ом.

Варианты ответа: 1. 2 В; 2. 1,2 В; 3. 1,8 В; 4. 3 В; 5. 3, 7 В.

4. Каким должно быть сопротивление шунта по сравнению с сопротивлением амперметра , если надо измерить общий ток в цепи 10 А, а амперметр имеет предел 2 А?

Варианты ответа:

1. R_ш = 0,25 R_А; 2. R_ш = R_А; 3. R_ш = 5R_А; 4. R_ш = 0,1R_А.

5. Две электрические лампочки с сопротивлением R₁ = 360 Ом и R₂ = 240 Ом включены в сеть параллельно. Какая из лампочек потребляет большую мощность и во сколько раз?

Варианты ответа: 1. Вторая, в 1,5 раза; 2. Первая в 1,5 раза;

3. Первая, в 2,25 раза; 4. Вторая, в 2,25 раза; 5. Первая, в 1,2 раза.

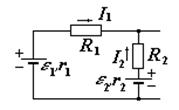
6. Какое из уравнений представляет второе правило Кирхгофа для данного контура? Ток через сопротивление R₁ идет слева - направо.

Варианты ответа:

1. I₁ (R₁+r₁) - I₂(R₂+r₂) = e₁ - e₂.

2. I₁ R₁ - I₂R₂ = e₁ - e₂.

3. -I₁ (R₁+r₁) - I₂(R₂+r₂) = e₁ + e₂.

4. I₁ (R₁+R₂) + I₂(r₁+r₂) = e₁ + e₂

З а м е ч а н и е : правильный ответ в задачах теста - под номером 1.

3.4. КОНТРОЛЬНАЯ РАБОТА № 3

№	Номера задач

300. В вершинах квадрата находятся одинаковые заряды q = З·10^-10 Кл каждый. Какой отрицательный заряд q₀ нужно поместить в центре квадрата, чтобы сила взаимного отталкивания положительных зарядов была уравновешена силой притяжения отрицательного заряда?

301. В вершинах шестиугольника со стороной а = 10 см расположены точечные заряды q, 2q, 3q, 4q, 5q, 6q (q = 0,1 мкКл). Найти силу F, действующую на точечный заряд q, лежащий в плоскости шестиугольника и равноудаленный от его вершин.

302. Четыре одинаковых заряда q = 40 нКл каждый закреплены в вершинах квадрата со стороной а = 10 см. Найти силу, действующую на один из этих зарядов со стороны трех остальных.

303. Три одинаковых заряда q = 10^-9 Кл каждый расположены по вершинам равностороннего треугольника. Какой отрицательный заряд q₀ нужно поместить в центре треугольника, чтобы его притяжение уравновесило силы взаимного отталкивания зарядов?

304. В вершинах квадрата находятся положительные одинаковые заряды q. В центр квадрата помещен отрицательный заряд q₀ = -0,287 нКл. Найти q, если результирующая сила, действующая на каждый заряд, равна нулю.

305. Сила взаимного гравитационного притяжения двух водяных одинаково заряженных капель уравновешивается силой электростатического отталкивания. Определить заряд q капель, если их радиусы r = 1,5·10^-4 м. ρ_воды = 10³ кг/м³.

306. В элементарной теории атома водорода принимают, что электрон обращается вокруг ядра по круговой орбите. Определить скорость электрона, если радиус орбиты R = 5,3·10^-9 см. Сколько оборотов в секунду делает электрон?

307. Заряд q = 3·10^-7 Кл равномерно распределен по сферической поверхности. Какую скорость нужно сообщить точечному заряду q₀ = 2·10^-9 Кл, массой m = 6·10^-6 кг в направлении, перпендикулярном, прямой, соединяющей центр сферической поверхности с точечным зарядом, чтобы он начал вращаться по окружности с радиусом r = 10 см, R_сф < r, m<<m_сф.

308. Два положительных заряда q₁ = 2 нКл и q₂ = 4 нКл находятся на расстоянии l = 60 см друг от друга. Определить местоположение, величину и знак заряда q₃, чтобы все заряды находились в равновесии.

309. Два одинаковых алюминиевых шарика радиусом R надеты на тонкий непроводящий стержень. Верхний шарик, имеющий заряд +q , закреплен, а нижний (его заряд -q) может свободно перемещаться вдоль стержня. На каком расстоянии r будут находиться в равновесии заряженные шарики при вертикальном положении стержня. (r>>R)

310. Треть тонкого кольца радиуса R = 10 см несет равномерно распределенный заряд q = 50 нКл. Определить напряженность 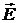и потенциал φ электрического поля, создаваемого распределенным зарядом в точке, совпадающей с центром кольца.

311 Тонкий стержень длиной l = 20 см несет равномерно распределенный заряд с линейной плотностью τ = 0,1 мкКл. Определить напряженность 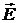и потенциал φ электрического поля, создаваемого распределенным зарядом в точке А, лежащей на оси стержня на расстоянии d = 20 см от его конца.

312. По дуге кольца длиной в шестую часть окружности распределен заряд q = 31,4 нКл. Определить напряженность 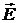и потенциал φ электрического поля, создаваемого распределенным зарядом в точке О, совпадающей с центром кольца. Радиус окружности R = 10 см.

313. По дуге кольца длиной в три четверти окружности распределен заряд с линейной плотностью τ = 20 нКл/м. Определить напряженность 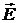и потенциал φ электрического поля, создаваемого распределенным зарядом в точке О, совпадающей с центром кольца. Радиус окружности R = 14,1 см.

314. Тонкое кольцо несет распределенный заряд q = 0,2 мкКл. Определить напряженность 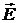и потенциал φ электрического поля, создаваемого распределенным зарядом в точке А, равноудаленной от всех точек кольца на расстояние r = 20 см. Радиус кольца R = 10 см.

315. По дуге кольца длиной в пять шестых окружности распределен заряд с линейной плотностью τ = 20 нКл/м. Определить напряженность 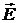и потенциал φ электрического поля, создаваемого распределенным зарядом в точке О, совпадающей с центром кольца. Радиус окружности R = 10 см.

316. Тонкий стержень, уходящий одним концом в бесконечность, несет равномерно распределенный заряд с линейной плотностью τ = 0,5 мкКл/м. Определить напряженность 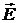и потенциал φ электрического поля, создаваемого зарядом стержня в точке А, лежащей на оси стержня на расстоянии а = 20 см от его начала.

317. Четверть тонкого кольца радиусом R = 10 см несет равномерно распределенный заряд q = 0,05 мкКл. Определить напряженность 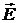и потенциал φ электрического поля, создаваемого распределенным зарядом в точке О, совпадающей с центром кольца.

318. Две трети тонкого кольца радиусом R = 10 см несут равномерно распределенный заряд с линейной плотностью τ= 0,2 мкКл/м. Определить напряженность 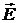и потенциал φ электрического поля, создаваемого распределенным зарядом в точке О, совпадающей с центром кольца.

319. По тонкому полукольцу радиуса R = 10 см равномерно распределен заряд с линейной плотностью τ = 1 мкКл/м. Определить напряженность 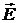и потенциал φ электрического поля, создаваемого распределенным зарядом в центре кольца.

320. На двух параллельных бесконечных плоскостях равномерно распределены заряды с поверхностными плотностями σ₁ = -4σ, σ₂ = 2σ, где σ = 40 нКл/м². 1) Найти напряженность Е электрического поля в трех областях: слева, между и справа от плоскостей; 2) на чертеже указать направление вектора 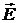для каждой области.

321. На двух концентрических сферах радиусом R и 2R равномерно распределены заряды с поверхностными плотностями σ₁ = σ и σ₂ = -σ, где σ = 0,1 мкКл/м². Требуется: 1) найти зависимость Е(r) напряженности электрического поля от расстояния от центра сфер для трех областей: внутри сфер, между сферами и вне сфер; 2) вычислить напряженность Е в точке, удаленной от центра на расстояние r = 3R и указать направление вектора .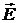

322. На двух бесконечных параллельных плоскостях равномерно распределены заряды с поверхностными плотностями σ₁ = 2σ и σ₂ = σ, где σ= 20 нКл/м. Требуется: 1) найти напряженность Е электрического поля в трех областях: слева от плоскостей, между плоскостями и справа от плоскостей; 2) на чертеже указать направление вектора 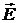для каждой области.

323. На двух бесконечных параллельных плоскостях равномерно распределены заряды с поверхностными плотностями σ₁ = σ, σ₂ = -2σ, где σ = 20 нКл/м². Требуется: 1) найти напряженность Е электрического поля в трех областях: слева, между и справа от плоскостей, 2) на чертеже указать направление вектора 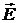для каждой области.

324. На двух концентрических сферах радиусами R и. 2R равномерно распределены заряды с поверхностными плотностями σ₁ = 4σ и σ₂ = σ, где σ = 30 нКл/м². Требуется: 1) найти зависимость Е(r) напряженности электрического поля от расстояния до центра сфер для трех областей: внутри сфер, между сферами и вне сфер; 2) вычислить напряженность Е в точке, удаленной от центра на расстояние r = 1,5 R и указать направление вектора .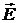

325. На двух коаксиальных бесконечных цилиндрах радиусами R и 2R равномерно распределены заряды с поверхностными плотностями σ₁ = -2σ и σ₂ = σ, где σ = 50 нКл/м². Требуется: 1) найти зависимость Е(r) напряженности электрического поля от расстояния до оси цилиндров для трех областей: внутри, между и вне цилиндров; 2) вычислить напряженность Е в точке, удаленной от оси цилиндров на расстояние r = 1,5 R и указать направление вектора .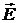

326. На двух концентрических сферах радиусом R и 2R равномерно распределены заряды с поверхностными плотностями σ₁ = -4σ и σ₂ = σ, где σ = 50 нКл/м². Требуется: 1) найти зависимость Е(r) напряженности электрического поля от расстояния до центра сфер для трех областей: внутри сфер, между сферами и вне сфер; 2) вычислить напряженность Е в точке, удаленной от центра на расстояние r = 1,5 R и указать направление вектора .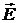

327. На двух коаксиальных бесконечных цилиндрах радиусами R и 2R равномерно распределены заряды с поверхностными плотностями σ₁ = σ и σ₂ = -σ, где σ = 60 мкКл/м². Требуется: 1) найти зависимость Е(r) напряженности электрического поля от расстояния до оси цилиндров для трех областей: внутри, между и вне цилиндров; 2) вычислить напряженность Е в точке, удаленной от оси цилиндров на расстояние r = 3R, и указать направление вектора .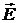

328. На двух коаксиальных бесконечных цилиндрах радиусами R и 2R равномерно распределены заряды с поверхностными плотностями σ₁ = -σ и σ₂ = 4σ, где σ = 30 НКл/м². Требуется: 1) найти зависимость Е(r) напряженности электрического поля от расстояния до оси цилиндров для трех областей: внутри, между и вне цилиндров; 2)вычислить напряженность Е в точке, удаленной от оси цилиндров на расстояние r = 4R, и указать направление вектора .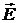

329. На двух концентрических сферах радиусом R и 2R равномерно распределены заряды с поверхностными плотностями σ₁ = -2σ и σ₂ = σ, где σ = 0,1 мкКл/м². Требуется: 1) найти зависимость напряженности электрического поля от расстояния до центра сфер для трех областей: внутри сфер, между сферами и вне сфер; 2) вычислить напряженность Е в точке, удаленной от центра на расстоянии r = 3R, и указать направление вектора .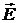

330. Четыре одинаковые капли ртути, заряженные до потенциала φ₁ = 10 В, сливаются в одну. Каков потенциал φ образовавшейся капли?

331. В однородное электрическое поле напряженностью Е = 200 В/м влетает вдоль силовых линий электрон со скоростью v₀ = 2 Мм/с. Определить расстояние l, которое пройдет электрон до точки, в которой его скорость будет равна половине начальной.

332. Электрическое поле создано бесконечной заряженной прямой линией с равномерно распределенным зарядом (τ = 10 нКл/м). Определить кинетическую энергию W_к2 электрона на расстоянии а, если на расстоянии 3а от линии его кинетическая энергия W_к1 = 200 эВ.

333. Шарик массой m = 40 мг, имеющий положительный заряд q = 1 нКл, движется со скоростью v = 10 см/с. На какое расстояние минимальное r может приблизиться шарик к положительному точечному заряду q₀ = 1,33 нКл?

334. Шарик массой m = 1 г и зарядом q = 10 нКл перемещается из точки 1, потенциал которой φ₁ = 600 В, в точку 2, потенциал которой φ₂ = 0. Найти его скорость в точке 1, если в точке 2 она стала равной v₂ = 20 см/с.

335. Найти скорость электрона, прошедшего разность потенциалов U, равную 100 В.

336. Электрон движется вдоль силовой линии однородного электрического поля. В некоторой точке поля с потенциалом φ₁ = 100 В электрон имел скорость v₁ = 6 Мм/с. Определить потенциал φ₂ точки поля, дойдя до которой электрон потеряет половину своей скорости.

337. Найти отношение скоростей ионов Cu⁺⁺ и К⁺, прошедших одинаковую разность потенциалов.

338. Электрон с энергией W = 400 эВ (в бесконечности) движется вдоль силовой линии по направлению к поверхности металлической заряженной сферы радиусом R = 10 см. Определить минимальное расстояние а, на которое приблизится электрон к поверхности сферы, если заряд ее q = -10 нКл.

339. Электрическое поле создано заряженным проводящим шаром, потенциал φ которого 300 В. Определить работу сил поля по перемещению заряда q = 0,2 мкКл из точки, отстоящей от поверхности шара на расстоянии R, до точки, отстоящей на расстоянии 3R.

340. Конденсатор электроемкостью С₁ = 0,6 мкФ был заряжен до разности потенциалов U₁ = 300 В и соединен параллельно со вторым конденсатором электроемкостью C₂ = 0,4 мкФ, заряженным до разности потенциалов U₂ = 160 В. Найти заряд, перетекший с пластин первого конденсатора на второй.

341. Конденсатор электроемкостью С₁ = 0,2 мкФ был заряжен до разности потенциалов U₁ = 320 В. После того, как его соединили параллельно со вторым конденсатором, заряженным до разности потенциалов U₂ = 450 В, напряжение на нем изменилось до 400 В. Вычислить емкость С₂ второго конденсатора.

342. Между пластинами плоского конденсатора находится плотно прилегающая стеклянная пластинка (ε = 7). Конденсатор заряжен до разности потенциалов U = 100 В. Какова будет разность потенциалов, если вытащить стеклянную пластинку из конденсатора?

343. К воздушному конденсатору, заряженному до разности потенциалов U₁ = 500 В и отключенному от источника напряжения, присоединили параллельно второй конденсатор таких же размеров и формы, но с другим диэлектриком (стекло). Определить диэлектрическую проницаемость стекла ε, если после присоединения второго конденсатора разность потенциалов уменьшилась до U₂ = 70 В

344. Два конденсатора емкостями С₁ = 5 мкФ и С₂ = 8 мкФ соединены последовательно и присоединены к батарее с э.д.с. ε = 80 В. Определить заряды q₁ и q₂ конденсаторов и разности потенциалов U₁ и U₂ между их обкладками.

345. Пластины плоского конденсатора изолированы друг от друга слоем диэлектрика. Конденсатор заряжен до разности потенциалов U = 1 кВ и отключен от источника напряжения. Определить диэлектрическую проницаемость диэлектрика, если при его удалении разность потенциалов между пластинами конденсатора возрастет до 3 кВ.

346. Три конденсатора (С₁ = 1 мкФ, С₂ = 2 мкФ, С₃ = 3 мкФ) соединены последовательно и присоединены к источнику напряжения (U = 220 В). Найти заряд и напряжение на каждом конденсаторе.

347. Два одинаковых плоских воздушных конденсатора емкостью С = 100 пФ каждый соединены в батарею последовательно. Определить, на сколько изменится емкость С батареи, если пространство между пластинами одного из конденсаторов заполнить парафином.

348. Пространство между пластинами плоского конденсатора заполнено двумя слоями диэлектрика: стекла толщиной d₁ = 0,2 см и парафина толщиной d₂ = 0,3 см. Разность потенциалов между обкладками U = 300 В. Определить напряженность Е поля и падение потенциала в каждом из слоев.

349. Два шара, радиусы которых 5 и 8 см, а потенциалы соответственно 120 и 50 В, соединяют проводом. Найти потенциалы шаров после их соединения и заряд, перешедший с одного шара на другой.

350. Плоский конденсатор с площадью пластин S = 300 см² каждая заряжен до разности потенциалов U = 10³ В. Расстояние между пластинами d = 4 см. Диэлектрик – стекло (ε = 7). Какую нужно совершить работу, чтобы удалить стекло из конденсатора? Конденсатор отключен от источника.

351. Энергия плоского воздушного конденсатора W₁ = 2·10^-7 Дж. Определить энергию конденсатора после заполнения его диэлектриком с диэлектрической проницаемостью ε = 2, если конденсатор отключен от источника питания.

352. Энергия плоского воздушного конденсатора W₁ = 4·10^-7 Дж. Определить энергию конденсатора после заполнения его диэлектриком с диэлектрической проницаемостью ε = 4, если конденсатор подключен к источнику питания.

353. Пластины плоского конденсатора подключены к источнику с э.д.с 2 В. Определить изменение энергии электрического поля конденсатора, если конденсатор наполовину заполнить диэлектриком с диэлектрической проницаемостью ε = 2. Граница между диэлектриком и воздухом расположена перпендикулярно пластинам. Расстояние между пластинами d = 1 см, площадь пластин S = 50 см².

354. Пластины плоского конденсатора подключены к источнику с э.д.с 2 В. Определить изменение энергии электрического поля конденсатора, если конденсатор наполовину заполнить диэлектриком с диэлектрической проницаемостью ε = 2. Граница между диэлектриком и воздухом расположена параллельно пластинам конденсатора. Расстояние между пластинами d = 1 см, площадь пластин S = 50 см².

355. Разность потенциалов между пластинами плоского конденсатора 100 В. Площадь каждой пластины 200 см², расстояние между пластинами 0,5 мм, пространство между ними заполнено парафином (ε = 2). Определить силу притяжения пластин друг к другу и энергию поля конденсатора.

356. Плоский конденсатор заполнен диэлектрикоми на егопластины подана некоторая разность потенциалов. Его энергия при этом равна 2·10^-5 Дж. После того как конденсатор отключили от источника напряжения, диэлектрик вынули из конденсатора. Работа, которую надо было совершить против сил электрического поля, чтобы вынуть диэлектрик, равна 7·10^-5 Дж. Найти диэлектрическую проницаемость диэлектрика.

357. Плоский воздушный конденсатор с площадью пластин 100 см² и расстоянием, между ними 1мм заряжен до 100 В. Затем пластины раздвигаются до расстояния 25 мм. Найти энергию конденсатора до и после раздвижения пластин, если источник напряжения перед раздвижением: 1) не отключается; 2) отключается.

358. Пять параллельно соединенных одинаковых конденсаторов емкостью по 0,1 мкФ заряжаются до общей разности потенциалов U = 30 кВ. Определить среднюю мощность разряда, если батарея разряжается за τ = 1,5·10^-6 с. Остаточное напряжение равно 0,5 кВ.

359. Плоский воздушный конденсатор с площадью пластины S = 400 см² подключен к источнику тока, э.д.с. которого равна 200 В. определить работу внешних сил по раздвижению пластин от расстояния d₁ = 2 см до d₂ = 4 см. Пластины в процессе раздвижения остаются подключенными к источнику.

360. Э.д.с. батареи 12 В, сила тока короткого замыкания 5 А. Какую наибольшую мощность можно получить во внешней цепи, соединенной с такой батареей?

361. Э.д.с. батареи ε = 80 В, внутреннее сопротивление r₁ = 5 Ом. Внешняя цепь потребляет мощность Р = 100 Вт. Определить силу тока I в цепи, напряжение U, под которым находится внешняя цепь, и ее сопротивление R.

362. Обмотка катушки из медной проволоки при t₁ = 14 ºС имеет сопротивление R₁ = 10 Ом. После пропускания тока сопротивление обмотки стало равным R₂ = 12,2 Ом. До какой температуры t₂ нагрелась обмотка? Температурный коэффициент сопротивления меди α = 4,15·10^-3 К^-1.

363. В сеть с напряжением U = 100 В подключили катушку с сопротивлением R₁ = 2 кОм и вольтметр, соединенные последовательно. Показание вольтметра U = 80 В. Когда катушку заменили другой, вольтметр показал U₂ = 60 В. Определить сопротивление R₂ другой катушки.

364. Э.д.с. батареи ε = 24 В, внутреннее сопротивление r = 2,4 Ом. Определить максимальную мощность Р_max, которая может выделяться во внешней цепи.

365. При внешнем сопротивлении R₁ = 8 Ом сила тока в цепи I₁ = 0,8 А, при сопротивлении R₂ = 15 Ом сила тока I₂ = 0,5 А. Определить силу тока I_кз короткого замыкания источника э.д.с.

366. Элемент, имеющий э.д.с. ε = 1,1 В и внутреннее сопротивление r = 1 Ом, замкнут на внешнее сопротивление R = 9 Ом. Найти ток I в цепи, падение потенциала U во внешней цепи и падение потенциала U_r внутри элемента. С каким к.п.д. η работает элемент?

367. Пять последовательно соединенных источников с э.д.с. ε = 1,2 В и внутренним сопротивлением 0,2 Ом каждый замкнуты на внешнее сопротивление R. Какой величины должно быть R, чтобы во внешней цепи выделялась максимальная мощность?

368. Сопротивление гальванометра R_Г = 720 Ом, шкала его рассчитана на 300 мкА. Как и какое добавочное сопротивление нужно подключить, чтобы можно было систему включать в цепь с напряжением 300 В?

369. Сопротивление гальванометра R_Г = 680 Ом. Какое сопротивление (шунт) нужно подключить к нему, чтобы можно было измерить ток силой 2,5 А? Шкала гальванометра рассчитана на 300 мкА.

370. Сила тока в проводнике равномерно убывает от 20 А до 6 А в течение 6 с. Какой заряд проходит через поперечное течение проводника за последние четыре секунды?

371. Определить напряженность электрического поля в алюминиевом проводнике объемом 10 см³, если при прохождении по нему постоянного тока за время 5 мин выделилось количество теплоты 2,3 кДж. Удельное сопротивление алюминия ρ = 26 нОм×м.

372. Сила тока в проводнике равномерно нарастает от I₀ = 0 до I = 5 А в течение времени 10 с. Определить заряд, прошедший по проводнику.

373. Определить количество теплоты Q, выделившееся за время t = 10 с в проводнике сопротивлением R = 10 Ом, если сила тока в нем, равномерно уменьшаясь, изменилась от I₁ = 10 А до I₂ = 0.

374. За время t = 8 с при равномерно возраставшей силе тока в проводнике сопротивлением R = 8 Ом выделилось количество теплоты Q = 500 Дж. Определить заряд q, прошедший в проводнике, если сила тока в начальный момент времени равна нулю.

375. За время t = 10 с при равномерно возрастающей силе тока от нуля до некоторого максимального значения в проводнике выделилось количество теплоты Q = 40 кДж. Определить среднюю силу тока <I> в проводнике, если его сопротивление R = 26 Ом.

376. Плотность электрического тока в медном проводе равна 10 А/см². Определить объемную плотность тепловой мощности тока, если удельное сопротивление меди ρ = 17 нОм×м.

377. В проводнике за время t = 10 с при равномерном возрастании силы тока от I₁ = 1 А до I₂ = 2 А выделилось количество теплоты Q = 5 кДж. Найти сопротивление R проводника.

378. Сила тока в проводнике сопротивлением R = 10 Ом за время t = 50 с равномерно нарастает от I₁ = 5 А до I₂ = 10 А. Определить количество теплоты Q, выделившееся за это время в проводнике.

379. За время t = 20 с при силе тока, равномерно возрастающей от нуля до некоторого максимума, в проводнике сопротивлением R = 5 Ом выделилось количество теплоты Q = 4 кДж. Определить скорость нарастания силы тока.

380. В схеме на рис. ε₁ = 2 В, ε₂ = 4 В, R₁=0,5 Ом и падение потенциала на сопротивлении R₂ (ток через R₂ направлен сверху вниз) равно 1 В. Найти показание амперметра. Внутренним сопротивлением элементов и амперметра пренебречь.

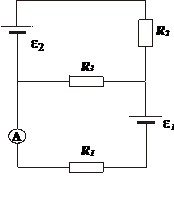
381. В схеме на рис. справа ε₁ = 30 В, ε₂ = 5 В, R₂ = 10 Ом, R₃ = 20 Ом. Через амперметр идет ток в 1 А, направленный от R₃ к R₁. Найти сопротивление R₁. Сопротивлением батареи и амперметра пренебречь.

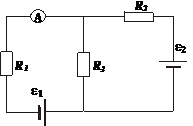
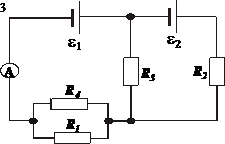382. В схеме на рис. ε₁ = ε₂ = 100 В, R₁ = 20 Ом, R₂ = 10 Ом, R₃ = 40 Ом, R₄ = 30 Ом. Найти показание амперметра. Сопро­тив­ле­нием батарей и ампер­метра пренебречь.

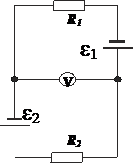383. В схеме на рис. ε₁ =ε₂, R₂ = 2R₁. Во сколько раз ток, текущий через вольтметр, больше тока, текущего через R₂? Сопротивлением генераторов пренебречь.

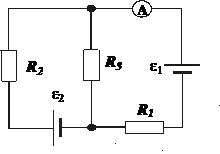384. В схеме на рис. ε₁ = ε₂ = 110 В, R₁ = 200 Ом, сопротивление вольтметра 1000 Ом. Найти показание вольтметра. Сопротивлением батареи пренебречь. R₂ = 100 Ом.

385. Какую силу тока показывает миллиамперметр мА в схеме на рис., если ε₁ = 2 В, ε₂ = 1 В, R₁ = 10³ Oм, R₂ = 500 Ом, R₃ = 200 Ом и сопротивление амперметра равно R_А = 200 Ом? Внутренним сопротивлением элементов пренебречь.

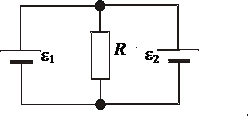386. Два элемента с одина­ковы­ми э.д.с. ε₁ = ε₂ = 2 В и внутренними сопротивлениями r₁ = 1 Ом и r₂ = 2 Ом замкнуты на внешнее сопротивление R (см. рис.). Через элемент с э.д.с. ε₁ течет ток I₁ = 1 А. Найти сопротивление R и ток I₂, текущий через элемент с э.д.с. ε₂. Какой ток I течет через сопротивление R?