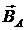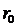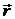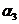Циркуляция вектора напряженности магнитного поля по замкнутому контуру равна алгебраической сумме токов, охватываемых этим контуром.
Алгебраическую сумму токов 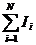 называютполным током.
называютполным током.
Положительным считается ток, направление которого связано с направлением обхода по контуру правилом правого винта; ток противоположного направления считается отрицательным.
Каждый ток учитывается столько раз, сколько раз он охватывается контуром. Например, согласно рис.1.8:
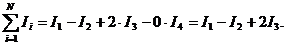
Магнитное поле соленоида
Используя закон полного тока, определим напряженность магнитного поля внутри соленоида длиной ℓ. Согласно выражению
(1.21) имеем Hℓ = NI, откуда
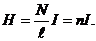 (1.22)
(1.22)
Индукция магнитного поля внутри соленоидаопределяется по формуле:
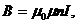 (1.23)
(1.23)
где n = N/ℓ - число витков, приходящихся на единицу длины соленоида (плотность витков).
По формуле (1.22) можно рассчитать напряженность магнитного поля тороида
(ℓ = 2πr –длина средней линии тороида):
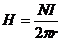 . (1.24)
. (1.24)
Индукция магнитного поля тороида:
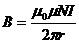 ,(1.25)
,(1.25)
где N – число витков тороида; r – радиус средней линии тороида.
Вопросы для самоконтроля
1. Дайте определение магнитного поля?
2. Что является силовой характеристикой магнитного поля?
3. Как связаны между собой напряженность и индукция магнитного поля?
4. Как графически изображается магнитное поле?
5. Сформулируйте и запишите математическое выражение закона Био – Савара – Лапласа.
6. По какому правилу определяется направление вектора магнитной индукции (напряженности) элемента тока?
7. Назовите единицы напряженности и индукции магнитного поля.
8. Сформулируйте и поясните принцип суперпозиции магнитных полей.
9. По какой формуле рассчитывается индукция (напряженность) магнитного поля, созданного:
- проводником с током конечной длины;
- бесконечно длинным проводником с током;
- круговым витком с током в его центре и в произвольной точке на его оси?
10. Сформулируйте, запишите выражение и поясните закон полного тока (теорему о циркуляции вектора напряженности магнитного поля).
11. Запишите выражение индукции (напряженности) магнитного поля соленоида, тороида
Примеры решения задач
Задача 1.Определить индукцию магнитного поля 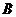 , созданного отрезком бесконечно длинного прямого проводника с током, в точке, равноудалённой от концов отрезка и находящейся на расстоянии
, созданного отрезком бесконечно длинного прямого проводника с током, в точке, равноудалённой от концов отрезка и находящейся на расстоянии 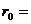 20 см от его середины. Сила тока, текущего по проводнику, I = 30 А, длина отрезка ℓ = 60 см.
20 см от его середины. Сила тока, текущего по проводнику, I = 30 А, длина отрезка ℓ = 60 см.
Дано: Решение.
 I = 30 АКаждый элемент тока(
I = 30 АКаждый элемент тока( 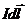 ) в данном случае
) в данном случае
создаёт индукцию 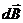 направленную в точке
направленную в точке
ℓ =60 см = 0,6 м А (см. рис.1.9) перпендикулярно плоскости
чертежа (к нам).
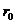 = 20 см = 0,2 м Все элементы индукции
= 20 см = 0,2 м Все элементы индукции 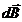 направлены в
направлены в
_______________ точке А одинаково, поэтому геометрическую
сумму всех векторов 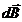 в точке А можно
в точке А можно
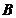 - ? заменить арифметической, т.е.
- ? заменить арифметической, т.е.  .
.
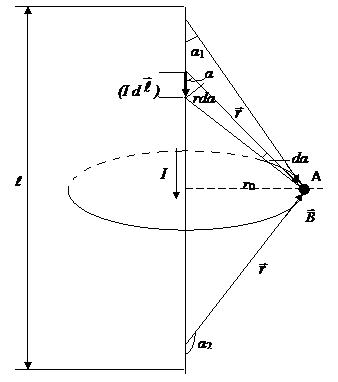
Рис.1.9
Запишем закон Био – Савара – Лапласа:
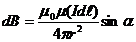 . (1.26)
. (1.26)
Преобразуем dB так, чтобы можно было взять интеграл по α, выразив 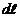 и r через
и r через  .
.
Из рис. 1.9 видно, что: 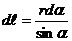 ,
, 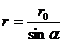 ,
,
где r – величина переменная, зависящая от угла α. Подставив 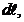 r в формулу (1.26), получим
r в формулу (1.26), получим
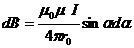 . (1.27)
. (1.27)
Проинтегрируем выражение (1.27) в пределах от 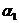 до
до 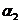 :
:
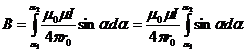 ;
;
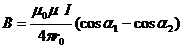 ,
,
где 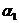 - угол между направлением начального элемента тока (
- угол между направлением начального элемента тока ( 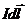 ) и направлением радиус – вектора
) и направлением радиус – вектора 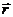 , проведённого от элемента тока к данной точке (угол острый);
, проведённого от элемента тока к данной точке (угол острый); 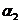 - угол между направлением конечного элемента тока (
- угол между направлением конечного элемента тока ( 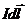 ) и направлением радиус–вектора
) и направлением радиус–вектора 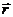 от элемента тока до данной точки (угол тупой).
от элемента тока до данной точки (угол тупой).
Из риc. 1.9 следует, что
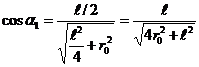 ;
;
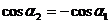 .
.
Тогда 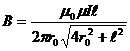 .
.
Вычислим В, подставив числовые значения:
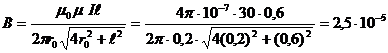 (Тл).
(Тл).
Ответ: 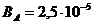 Тл.
Тл.
Задача 2.По двум длинным прямолинейным проводникам, находящимся на расстоянииd =10 см друг от друга в воздухе, текут токи силой I = 15 А каждый. Определить магнитную индукцию В поля, создаваемого токами в точке, лежащей посередине между проводниками, для следующих случаев: 1)проводники параллельны, токи текут в одном направлении (рис. 1.10 а); 2)проводники параллельны, токи текут в противоположных направлениях (рис. 1.10 б); 3)проводники взаимно перпендикулярны, направления токов указаны на рис. 1.10 в.
 Дано: Решение.
Дано: Решение.
 d= 10 см = 0,1 м
d= 10 см = 0,1 м
 I = 15 А
I = 15 А
r  = r
= r 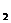 =
= 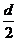 = 5
= 5 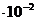 м
м
___________________
В - ?
а)
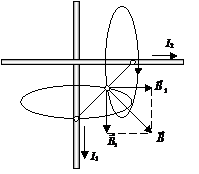 |
б)
в)
Рис. 1.10 а), б), в)
Результирующая индукция магнитного поля 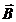 равна векторной сумме:
равна векторной сумме: 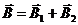 ,где
,где 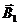 -индукция поля, создаваемого током
-индукция поля, создаваемого током 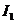 ;
; 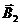 -индукция поля, создаваемого током I
-индукция поля, создаваемого током I 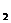 . Если
. Если 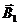 и
и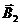 направлены по одной прямой, то векторная сумма может быть заменена алгебраической суммой:
направлены по одной прямой, то векторная сумма может быть заменена алгебраической суммой:
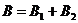 (1.28)
(1.28)
При этом слагаемые B1и B2должны быть взяты с соответствующими знаками. В данной задаче во всех трёх случаях абсолютные значения индукций B1и B2 одинаковы, так как точки выбраны на равных расстояниях от проводников, по которым текут равные токи. Вычислим эти индукции по формуле
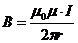 , (1.29)
, (1.29)
где r = r  = r
= r  ;
; 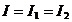 ;
; 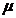 =1. Подставив числовые значения величин в формулу (1.29), найдём модули B1и B2:
=1. Подставив числовые значения величин в формулу (1.29), найдём модули B1и B2:
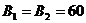 мкТл.
мкТл.
1-й случай.Векторы 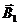 и
и 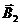 направлены по одной прямой (рис.1.10 а), следовательно, результирующая индукция
направлены по одной прямой (рис.1.10 а), следовательно, результирующая индукция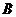 определяется по формуле (1.28). Приняв направление вверх положительным, вниз – отрицательным, запишем:
определяется по формуле (1.28). Приняв направление вверх положительным, вниз – отрицательным, запишем: 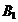 =60 мкТл,
=60 мкТл, 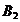 = -60 мкТл. Подставив в формулу (1.28) эти значения B1и B2 получим
= -60 мкТл. Подставив в формулу (1.28) эти значения B1и B2 получим
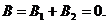
2-й случай.Векторы 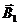 и
и 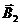 направлены по одной прямой в одну сторону (рис.1.10 б). Подставив в формулу (1.28) значения B1и B2, получим
направлены по одной прямой в одну сторону (рис.1.10 б). Подставив в формулу (1.28) значения B1и B2, получим
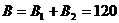 (мкТл).
(мкТл).
3-й случай.Векторы индукций магнитных полей, создаваемых токами в точке, лежащей на одинаковом расстоянии от проводников, взаимно перпендикулярны (рис.1.10 в). Результирующая индукция по абсолютному значению и направлению является диагональю квадрата, построенного на векторах 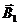 и
и 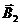 . По теореме Пифагора найдём
. По теореме Пифагора найдём
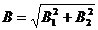 (1.30)
(1.30)
Подставив в формулу (1.30) значения B1и B2 и вычислив, получим
В = 84,6 (мкТл).
Ответ:1) В = 0; 2) В = 120 мкТл; 3) В = 84,6 мкТл.
Задача 3.По двум бесконечно длинным прямым параллельным проводникам, расстояние между которыми d = 15 см, текут токи I1 = 70 А и I2 = 50 А в одном направлении. Определить магнитную индукцию В в точке, удалённой на расстояние 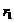 = 10 см от первого и на расстояние
= 10 см от первого и на расстояние 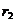 = 20 см от второго проводника.
= 20 см от второго проводника.
 Дано: Решение.
Дано: Решение.  см = 0,15 м
см = 0,15 м

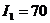 А
А
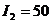 А
А
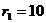 см = 0,1 м
см = 0,1 м
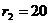 см = 0,2 м
см = 0,2 м
_________________ D
В - ? C
Рис.1.11
Для того, чтобы найти магнитную индукцию в указанной точке А (рис.1.11), определим направления векторов индукций 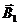 и
и 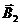 полей, создаваемых каждым проводником в отдельности в точке А.
полей, создаваемых каждым проводником в отдельности в точке А. 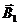
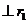 ,
, 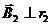 , т.к.
, т.к. 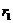 и
и 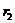 - радиусы силовых линий (от токов
- радиусы силовых линий (от токов 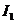 и
и 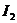 ), проведенные в точку касания, а
), проведенные в точку касания, а 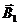 и
и 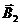 являются касательными к силовым линиям. На рис.1.11 токи
являются касательными к силовым линиям. На рис.1.11 токи 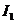 и
и 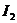 перпендикулярны плоскости чертежа и идут «к нам».
перпендикулярны плоскости чертежа и идут «к нам».
По принципу суперпозиции 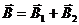 . Векторы
. Векторы 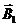 и
и 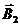 сложим по правилу параллелограмма, диагональ которого является результирующим вектором
сложим по правилу параллелограмма, диагональ которого является результирующим вектором 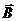 . Модуль вектора
. Модуль вектора 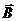 найдём по теореме косинусов:
найдём по теореме косинусов:
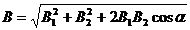 (1.31)
(1.31)
где α – угол между векторами 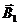 и
и 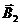 .
.
Значения индукций B1и B2 полей, созданных прямыми бесконечно длинными проводниками с токами 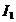 и
и 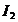 определяются по формулам:
определяются по формулам:
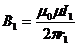 ;
; 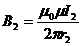 , (1.32)
, (1.32)
где 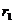 ,
, 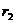 - кратчайшие расстояния от токов I1, I2 соответственно до точки, в которой определяется магнитная индукция В. Подставим (1.32) в (1.31):
- кратчайшие расстояния от токов I1, I2 соответственно до точки, в которой определяется магнитная индукция В. Подставим (1.32) в (1.31):
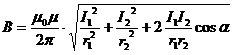 . (1.33)
. (1.33)
На рис.1.11 углы 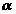 равны, как углы со взаимно перпендикулярными сторонами. Поэтому соs
равны, как углы со взаимно перпендикулярными сторонами. Поэтому соs 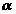 найдем из треугольника АDС по теореме косинусов
найдем из треугольника АDС по теореме косинусов 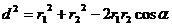 , отсюда
, отсюда
cos 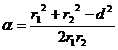 .
.
Вычислим соs 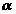 : cos
: cos 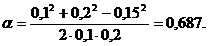
Определим индукцию В, подставив числовые значения в формулу (1.33):
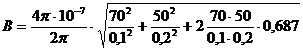 = 178 (мкТл).
= 178 (мкТл).
Ответ:В = 178 мкТл.
Задача 4. По длинному прямому проводнику, согнутому под прямым углом, течет токI = 5A.Найти магнитную индукцию B в точке, лежащей на биссектрисе угла и, отстоящей от вершины угла на расстояние а = 10 см (рис.1.12).
|

|

|
|
|

|

|

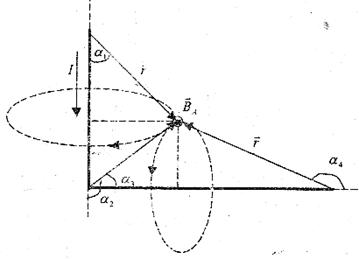
Рис. 1.12
 Дано: Решение.
Дано: Решение.
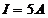 Изобразим силовые линии индукции
Изобразим силовые линии индукции
магнитного поля для каждого отрезка провод-
а = 10 см = 0,1 м ника. Линии должны проходить через задан-
ную точку, лежать в плоскости, перпендику-
 лярной току, и иметь центр на оси проводни-
лярной току, и иметь центр на оси проводни-
В 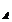 - ? с током (рис. 1.12). Направление линий индукции определим по правилу правого винта. Касательные к силовым линиям в данной точке перпендикулярны плоскости чертежа и векторы
- ? с током (рис. 1.12). Направление линий индукции определим по правилу правого винта. Касательные к силовым линиям в данной точке перпендикулярны плоскости чертежа и векторы 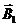 и
и 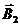 направлены «к нам».
направлены «к нам».
Согласно принципу суперпозиции 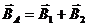 т.к.
т.к. 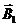 и
и 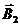 направлены в одну сторону по одной прямой, то
направлены в одну сторону по одной прямой, то 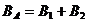 .
.
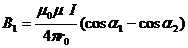 - индукция от вертикальной части провода;
- индукция от вертикальной части провода; 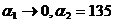 ˚, т.к. проводник в нижней части ограничен вершиной угла, а в верхней части бесконечен.
˚, т.к. проводник в нижней части ограничен вершиной угла, а в верхней части бесконечен.
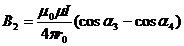 - индукция от горизонтальной части провода,
- индукция от горизонтальной части провода, 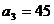 ˚,
˚, 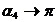 , т.к. провод ограничен вершиной угла слева и бесконечен справа
, т.к. провод ограничен вершиной угла слева и бесконечен справа
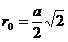 - кратчайшее расстояние от вертикального и горизонтального проводов до данной точки А, находящейся на биссектрисе угла.
- кратчайшее расстояние от вертикального и горизонтального проводов до данной точки А, находящейся на биссектрисе угла.
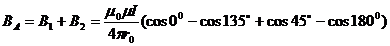 .
.
Подставим в данную формулу числовые значения и вычислим магнитную индукцию:
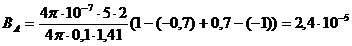 ( Тл).
( Тл).
Ответ: 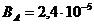 Тл.
Тл.
Задача 5.По двум одинаковым круговым виткам радиусом R = 5 см, плоскости которых взаимно перпендикулярны, а центры совпадают, текут одинаковые токи силой I = 2 А (рис.1.13). Найти индукцию магнитного поля в центре витков.
Дано: Решение.
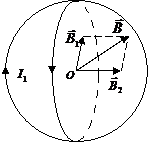 R = 5 см = 5·10
R = 5 см = 5·10  м
м
 =
=  I = 2 A
I = 2 A
 _________________
_________________
В - ?
Рис. 1.13
Индукцию магнитного поля, созданного каждым круговым витком в центре соответствующего витка, находим по формуле:
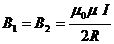 (1.34)
(1.34)
По правилу буравчика для выбранных направлений токов в витках вектор 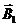 направлен от нас, а вектор
направлен от нас, а вектор 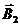 направлен вправо
направлен вправо
(см. рис. 1.13). По принципу суперпозиции результирующая индукция магнитного поля: 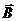 =
= 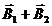 .
.
Поскольку векторы 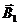 и
и 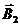 взаимно перпендикулярны, то по теореме Пифагора из соответствующего прямоугольного треугольника находим
взаимно перпендикулярны, то по теореме Пифагора из соответствующего прямоугольного треугольника находим
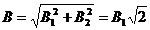 .(1.35)
.(1.35)
Подставив выражение (1.34) в (1.35), получим:
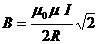 .
.
Вычислим: 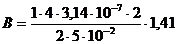 = 35,4 (мкТл).
= 35,4 (мкТл).
Ответ:В = 35,4 мкТл.
Задача 6.Требуется изготовить соленоид длиной L= 20 см и диаметром D = 5 см, создающий на своей оси магнитную индукцию B = 1,26 мТл. Найти разность потенциалов U, которую надо приложить к концам обмотки соленоида. Для обмотки применяют проволоку диаметром d = 0,5 мм. Удельное сопротивление меди ρ = 1,7 ∙ 10-8 Ом·м.
 Дано: Решение
Дано: Решение
D = 5 см = 5 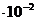 Разность потенциалов на концах обмотки
Разность потенциалов на концах обмотки
L = 20 см = 0,2 м соленоида
В =1,26 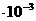 Тл U = IR. (1.36)
Тл U = IR. (1.36)
d = 0,5 мм = 5 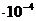 м Из выражения индукции магнитного по-
м Из выражения индукции магнитного по-
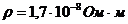 ля соленоида
ля соленоида 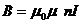 найдём силу
найдём силу
__________________ тока, текущего по соленоиду:
U - ? 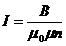 , (1.37)
, (1.37)
где n = N/L – плотность витков (количество витков на единицу длины).
Поскольку полное число витков соленоида N = L/d, выражение (1.37) можно привести к виду
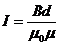 . (1.38)
. (1.38)
Сопротивление обмотки найдём по формуле
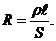 (1.39)
(1.39)
Здесь ℓ = πDN = πDL/d – длина обмотки (проволоки) соленоида;
S = πd²/4 – площадь поперечного сечения проволоки;
ρ – удельное сопротивление меди.
Подставив эти выражения в формулу (1.39), найдём
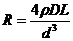 (1.40)
(1.40)
Преобразуя уравнение (1.36) с помощью формул (1.38) и (1.40), получим выражение для разности потенциалов на концах обмотки соленоида:
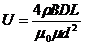 .
.
Вычислим: 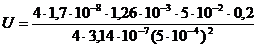 = 2,7 (В).
= 2,7 (В).
Ответ:U = 2,7 В.
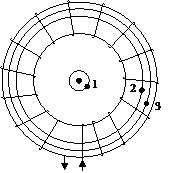
Задача 7.По тороидальной катушке с числом витков N = 1000 течёт ток I = 5 А. Cредний диаметр катушки d = 40 см, радиус витков r = 5 см. Определить напряжённость Н магнитного поля вточках, находящихся от центра тороида на расстояниях а1 = 5 см, а2 = 20 см и а3 = 23 см.
 Дано: Решение.
Дано: Решение.
N = 1000 Воспользуемся теоремой о циркуляции
вектора напряжённости магнитного
I = 5 А поля. В качестве контуров интегрирования
возьмём окружности с центрами в центре
d = 40 см = 0,4 м тороида и радиусами, равными расстоянию
от центра тороида до заданных точек
r = 5 cм = 5 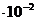 м (см. рис.1.14). Точка 1 находится на рассто-
м (см. рис.1.14). Точка 1 находится на рассто-
янии 5 см от центра тороида. Окружность,
а 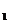 = 5 см = 5
= 5 см = 5 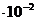 м проведённая через эту точку, не будет
м проведённая через эту точку, не будет
охватывать ток, поэтому
 а
а  = 0,23 м H1 = 0 (1.41)
= 0,23 м H1 = 0 (1.41)
а  = 0,2 м
= 0,2 м
___________________
Н  , Н
, Н  , Н
, Н  - ?
- ?
Рис. 1.14
Точка2 лежит на окружности, радиус которой равен среднему радиусу тороида (2а  = d). Плоскость, охватываемую этим контуром, пересекают N витков с током I, следовательно,
= d). Плоскость, охватываемую этим контуром, пересекают N витков с током I, следовательно,
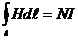 или
или 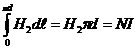 ,
,
откуда
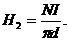 (1.42)
(1.42)
Точка 3 лежит внутри тороида, но находится на расстоянии 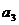 >
> 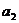 . Проведя рассуждения, аналогичные предыдущим, получим:
. Проведя рассуждения, аналогичные предыдущим, получим:
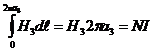
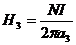 . (1.43)
. (1.43)
Подставив числовые значения в (1.42) и (1.43), получим
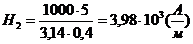 ;
; 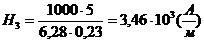 .
.
При заданных размерах катушки поле внутри тороида не будет однородным. Оно максимально у внутренней стороны обмотки и уменьшается по мере приближения к наружной стороне обмотки.
Ответ: Н1 = 0; Н 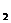 = 3,98
= 3,98 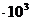 А/м; Н
А/м; Н 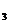 = 3,46
= 3,46 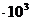 А/м.
А/м.
Задачи для самостоятельного решения
Магнитное поле прямого тока
Задача 1.1.Определить магнитную индукцию В поля, создаваемого отрезком бесконечно длинного проводника в точке, равноудалённой от концов отрезка и находящейся на расстоянии 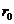 = 4 см от его середины. Длина отрезка проводника ℓ = 20 см, а сила тока в проводнике I = 10 А.
= 4 см от его середины. Длина отрезка проводника ℓ = 20 см, а сила тока в проводнике I = 10 А.
Ответ:В = 46,5 мкТл.
Задача 1.2.По двум бесконечно длинным прямым параллельным проводникам, находящимся на расстоянии d =10 см друг от друга в вакууме, текут токи 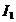 = 20 А и
= 20 А и 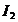 = 30 А одинакового направления. Определить магнитную индукцию B поля, создаваемого токами в точках, лежащих на прямой, соединяющей оба проводника, если
= 30 А одинакового направления. Определить магнитную индукцию B поля, создаваемого токами в точках, лежащих на прямой, соединяющей оба проводника, если  1) точка лежит на расстоянии
1) точка лежит на расстоянии 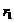 = 2 см левее левого проводника; 2) точка лежит на расстоянии
= 2 см левее левого проводника; 2) точка лежит на расстоянии 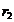 = 3 см правее правого проводника;
= 3 см правее правого проводника;
Ответ:1)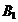 =0,25 мТл; 2)
=0,25 мТл; 2) 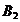 = 0,23 мТл;
= 0,23 мТл;
Задача 1.3. По двум бесконечно длинным прямым параллельным проводникам, находящимся на расстоянии d = 9 см друг от друга в вакууме, текут токи 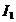 = 10 А и
= 10 А и 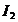 = 20 А одинакового направления. Определить магнитную индукцию B поля, создаваемого токами в точках, лежащих на прямой, соединяющей оба проводника, если точка лежит на расстоянии
= 20 А одинакового направления. Определить магнитную индукцию B поля, создаваемого токами в точках, лежащих на прямой, соединяющей оба проводника, если точка лежит на расстоянии 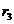 = 3 см правее левого проводника.
= 3 см правее левого проводника.
Ответ: 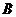 = 0.
= 0.
Задача 1.4. По двум бесконечно длинным прямым проводникам, скрещенным под прямым углом, текут токи силой 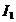 = 30 А и
= 30 А и 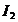 = 40 А. Расстояние между проводниками
= 40 А. Расстояние между проводниками 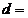 20 см. Определить магнитную индукцию B в точке, одинакового удаленной от обоих проводников на расстояние, равное d.
20 см. Определить магнитную индукцию B в точке, одинакового удаленной от обоих проводников на расстояние, равное d.
Ответ:B=50 мкТл.
Задача 1.5. Бесконечный прямой проводник с током 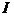 = 30 А согнут под прямым углом. Определить индукцию магнитного поля В в точке, лежащей на продолжении горизонтальной части проводника, на расстоянии а = 30 см от вершины угла.
= 30 А согнут под прямым углом. Определить индукцию магнитного поля В в точке, лежащей на продолжении горизонтальной части проводника, на расстоянии а = 30 см от вершины угла.
Ответ:В = 10 мкТл.
Задача 1.6.По бесконечно длинному прямому проводнику, изогнутому так, как это показано на рис.1.15 , течёт ток силой I = 120 А. Определить магнитную индукцию В в точке А, если R = 10 см. Закругление представляет собой четверть окружности.
Ответ:В = 0,99 мкТл.
Задача 1.7.По бесконечно длинному прямому проводнику, согнутому под углом  = 120º (рис.1.16), течёт ток силой I = 100 A. Найти магнитную индукцию В в точках, лежащих на биссектрисе угла, и удалённых от его вершины на расстояние а = 10 см.
= 120º (рис.1.16), течёт ток силой I = 100 A. Найти магнитную индукцию В в точках, лежащих на биссектрисе угла, и удалённых от его вершины на расстояние а = 10 см.
Ответ: 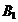 = 0,35 мТл;
= 0,35 мТл; 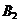 = 0,12 мТл.
= 0,12 мТл.
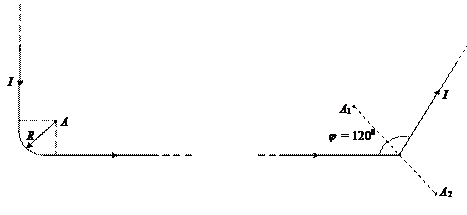 Рис.1.15 Рис.1.16
Рис.1.15 Рис.1.16
Задача 1.8.По двум бесконечно длинным прямым параллельным проводникам, расстояние между которыми d = 20 см, текут токи  = 40 А и
= 40 А и  = 80 А в одном направлении. Определить магнитную индукцию В в точке, удалённой от первого проводника на
= 80 А в одном направлении. Определить магнитную индукцию В в точке, удалённой от первого проводника на 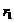 = 12 см и от второго на
= 12 см и от второго на 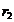 = 16 см.
= 16 см.
Ответ:В = 120 мкТл.
Задача 1.9.Два длинных параллельных проводника находятся на расстоянии d = 5 см один от другого. По проводникам текут в противоположных направлениях одинаковые токи силой I = 10А каждый. Найти напряженность Н магнитного поля в точке, находящейся на расстоянии 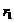 = 2 см от одного и
= 2 см от одного и 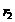 = 3 см от другого проводника.
= 3 см от другого проводника.
Ответ:Н =132 А/м.
Задача 1.10.По двум бесконечно длинным прямым параллельным проводникам текут токи силой 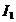 = 20 А и
= 20 А и 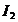 = 30 А в одном направлении. Расстояние d между проводниками равно 10 см. Вычислить магнитную индукцию поля В в точке, удалённой от обоих проводников на одинаковое расстояние r = 10 см.
= 30 А в одном направлении. Расстояние d между проводниками равно 10 см. Вычислить магнитную индукцию поля В в точке, удалённой от обоих проводников на одинаковое расстояние r = 10 см.
Ответ:В = 87,2 мкТл.
Задача 1.11.Определить индукцию магнитного поля B в центре проволочной квадратной рамки со стороной а = 15 см, если по рамке течёт ток I = 5 А.
Ответ:В = 37,3 мкТл.
Задача 1.12.По тонкому проводу, изогнутому в виде прямоугольника, течёт ток силой I = 60 А. Длины сторон прямоугольника: а = 30 см и b = 40 см. Определить магнитную индукцию В в точке пересечения диагоналей.
Ответ:В =200 мкТл.
Задача 1.13.По контуру в виде равностороннего треугольника течёт ток силой I =40 А. длина стороны треугольника равна 30 см. Определить магнитную индукцию В в точке пересечения высот.
Ответ:В = 240 мкТл.
Задача 1.14.По проводу, согнутому в виде правильного шестиугольника с длиной стороны, равной 20 см, течет ток силой I = 100 А. Найти напряженность Н магнитного поля в центре шестиугольника.
Ответ:Н=276 А/м.
Задача 1.15.Проводник согнут в виде ромба со стороной а = 4 см. Углы при вершинах ромба равны 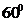 и
и 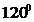 . Определить магнитную индукцию В поля в точке пересечения диагоналей ромба, если ток I в проводнике равен 30 А.
. Определить магнитную индукцию В поля в точке пересечения диагоналей ромба, если ток I в проводнике равен 30 А.
Ответ:В = 0,94 мТл.
Задача 1.16.По двум длинным параллельным прямым проводникам текут токи 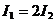 . Определить точку, в которой индукция магнитного поля равна нулю, если токи текут в одном направлении. Расстояние между проводниками равно а.
. Определить точку, в которой индукция магнитного поля равна нулю, если токи текут в одном направлении. Расстояние между проводниками равно а.
Ответ:x = 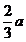 .
.
Задача 1.17.По двум длинным параллельным прямым проводникам текут токи 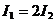 .Определить точку, в которой индукция магнитного поля равна нулю, если токи текут в противоположныхнаправлениях. Расстояние между проводниками равно а.
.Определить точку, в которой индукция магнитного поля равна нулю, если токи текут в противоположныхнаправлениях. Расстояние между проводниками равно а.
Ответ:х=2 а.