Второй закон Ньютона в неинерциальной системе отсчета. Силы инерции

Если тело находится в движущейся с ускорением 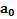неинерциальнойсистеме отсчета (НИСО), в которой оно движется с ускорением 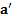,то его полное ускорение в неподвижной СО равно 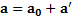.Тогда второй закон Ньютона для него в неподвижной СО: 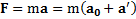можно записать в ускоренно движущейся СО, который примет вид: 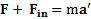,где введена сила 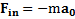,называемая силой инерции, направленная противоположно ускорению 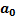ускоренно движущейся СО.

Задачи в НИСО решаются также, как в обычной ИСО. Только в этом случае ко всем внешним силам, действующим на тело, надо добавить силу инерции 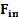и заменить во втором законе Ньютона ускорение 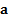на ускорение 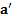тела в ускоренно движущейся СО.

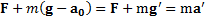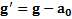Если на тело в неинерциальной СО действует сила тяжести, то второй закон в ней можно записать в виде ,где – ускорение свободного падения тела в НИСО. Согласно принципу эквивалентности Эйнштейна, находясь в ускоренно движущейся системе отсчета, никакими опытами нельзя определить, движется ли она ускоренно или находится в новом гравитационном поле.

Сила инерции 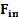, появляющаяся в ускоренно движущейся СО, не обусловлена взаимодействием движущегося тела с другими телами, а поэтому не имеет противодействующей по третьему закону Ньютона.

Пример 1. Тело массой 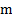подвешено на нити к потолку движущегося вверх или вниз с ускорением 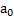лифте. Найти вес тела.

Дано: 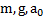. Найти: P― ?

Решение: В ускоренно движущейся СО тело находится в гравитационном поле с ускорением свободного падения .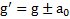

Рис.27

Тогда вес тела в соответствии с третьим законом Ньютона 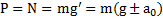, где 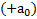соответствует ускоренному движению лифта вверх, а 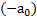– вниз. Вес тела Pприложен к нити, а не к телу, поэтому не показан на рис.27.

Ответ: .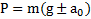

Пример 2: Тело массой 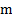подвешено на нити к потолку движущегося в горизонтальном направлении с ускорением 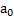лифте. Найти угол отклонения нити от вертикали и натяжение нити.

Дано: 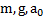.Найти: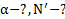

Решение:В ускоренно движущейся СО на тело действуют реакция нити 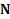, сила тяжести 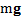и сила инерции 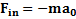либо реакция нити 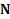и новая сила тяжести 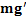,где 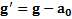– новое ускорение свободного падения.

Рис.28

Согласно рис.28 величи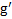на равна 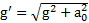и натяжение нити 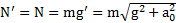. Угол отклонения нити от вертикали определяется условием 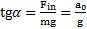. Сила натяжения нити 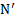приложена к нити, а не к телу и не показана на рис.28.

Ответ: , .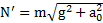

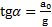Пример 3:Шар массой mнаходится на полу вагонетки, движущейся с ускорением 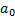, и прикреплен пружиной с жесткостью k к ее боковой стенке. Найти растяжение 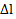пружины. Трение между полом и шаром отсутствует.

Дано: 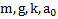.Найти: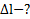

Решение:Второй закон Ньютона для шара в НИСО, связанной с вагонеткой (рис.29), имеет вид

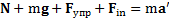, где 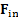– сила инерции.

Рис.29

При покое тела 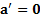,и второй закон для шаров проекциях на направление движения вагонетки будет иметь вид 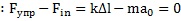, откуда находим Ответ: .

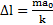Пример 4. На параллелепипед массой M, находящийся на горизонтальной поверхности, положено тело массой m. К телу прикладывают внешнюю горизонтальную силу F и система тело-параллелепипед приходит в движение. Найти ускорение параллелепипеда относительно земли и ускорение тела, с которым оно будет двигаться относительно него. Коэффициент трения между телом и параллелепипедом равен μ. Трение между параллелепипедом и горизонтальной поверхностью отсутствует.

Дано:m, M,F, g, µ. Найти: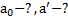

Решение:Для решения задачи выберем две системы отсчета: неподвижную XOY, связанную с горизонтальной поверхностью, и движущуюся вместе с параллелепипедом СО 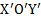(рис.30).

Рис.30

Как только система двух тел под действием силы Fпридет в движение, то параллелепипед начнет двигаться с ускорением 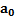и тело окажется в ускоренно движущейся СО и на него подействует сила инерции 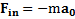.Между телами действуют силы трения 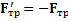,равные .

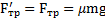Второй закон Ньютона для параллелепипеда будет иметь вид 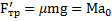. Откуда ускорение параллелепипеда .

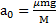Второй закон Ньютона для тела: 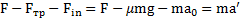. Откуда ускорение тела относительно параллелепипеда

,

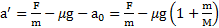если выполняется условие .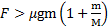

Ответ: , .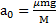

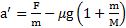Пример 5.Решить предыдущую задачу в предположении, что внешняя сила F приложена к параллелепипеду.

Дано:m, M,F, g, μ.Найти: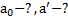

Решение: В данном случае направления сил 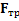и 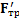, а также ускорения 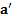тела поменяются на противоположные (рис.31).

Рис.31

Параллелепипед движется под действием сил 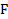и 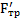и второй закон Ньютона для него (в проекциях на направление 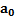) имеет вид 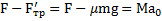. Откуда ускорение параллелепипеда .

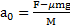Тело движется под действием сил 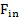и 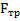, и второй закон Ньютона для него (в проекциях на направление 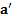) имеет вид

.

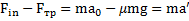Откуда ускорение тела относительно параллелепипеда

,

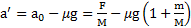если выполняется условие .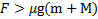

Ответ: , .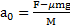

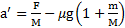Пример 6: Тело массой m находится на наклонной плоскости с углом наклона α, стоящей на горизонтальной поверхности. Плоскость под действием внешней силы приводят в движение с ускорением 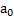в направлении ее острого угла вдоль горизонтальной поверхности.Найти ускорение 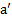, с которым тело будет двигаться вдоль наклонной плоскости (вверх или вниз), и новую силу тяжести 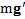, действующую на него, а также ее направление 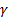по отношению к направлению силы тяжести 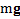до начала ускоренного движения наклонной плоскости.

Дано: 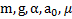.Найти: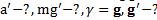

Решение:Выберем ось 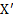ускоренно движущейся системы отсчета 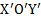, связанной с наклонной плоскостью, параллельно наклонной плоскости вверх, а ось 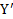перпендикулярно к ней (рис.32).

Рис.32

Второй закон Ньютона для тела в этой СО 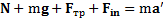в проекциях на ось 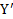имеет вид 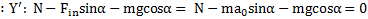. Откуда находим реакцию 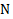наклонной плоскости и силу трения 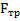между телом и плоскостью:

, .

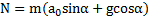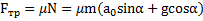Второй закон Ньютона в проекциях на ось 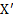имеет вид

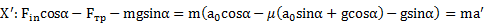
или 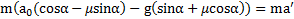. Откуда ускорение 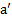движения тела вдоль наклонной плоскости

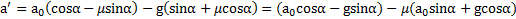
По выбору направления оси 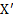: если 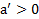, то ускорение тела направленно вверх, а если 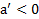, то вниз. При 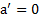тело будет на наклонной плоскости покоиться.

Ускорение свободного падения 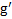в НИСО согласно рис.32 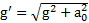, а угол 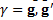определяется условием 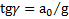или .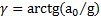

Ответ: , , .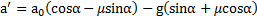

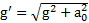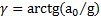Пример 7. Тело массой m соскальзывает с наклонной плоскости массой M и углом наклона α. Трение между телом и плоскостью и наклонной плоскостью и поверхностью, на которой она стоит, отсутствует. Найти ускорение соскальзывания тела с наклонной плоскости и ускорение, с которым движется наклонная плоскость.

Дано: 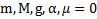.Найти: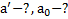

Решение:При соскальзывании тела с наклонной плоскости она придет в движение с ускорением 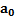и на тело, оказавшееся в ускоренно движущей СО, подействует сила инерции 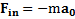.На него также действуют сила тяжести mgи реакция N наклонной плоскости (рис.33). По условию 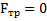. Второй закон Ньютона для тела в движущейся СО будет иметь вид .

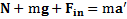Рис.33

На наклонную плоскость действует сила тяжести 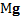и сила давления 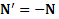тела на нее, и второй закон Ньютона для плоскости в неподвижной СО будет иметь вид .

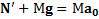Для решения задачи выберем две СО: неподвижную XOY, связанную с поверхностью, на которой находится наклонная плоскость, ось X которой направлена по ускорению 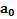наклонной плоскости, и движущуюся СО 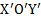, связанную с движущейся наклонной плоскостью, ось 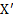которой направлена по ускорению 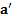соскальзывания тела с наклонной плоскости.

Спроецируем силы, действующие на тело, на ось 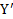движущейся СО. Получим

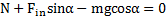. Откуда реакция наклонной плоскости, действующая на тело, и сила давления тела на плоскость равны

.

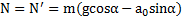Проецируя силы, действующие на наклонную плоскость, на ось X неподвижной СО, получим

.

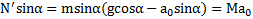Откуда ускорение наклонной плоскости .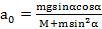

Второй закон Ньютона для тела в проекциях на ось 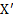движущейся СО будет иметь вид

.

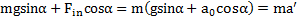Откуда ускорение 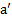, с которым тело соскальзывает с наклонной плоскости, будет равно

.

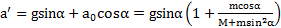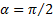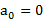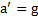При , как и должно быть, и . Ускорения плоскости и тела связаны соотношением .

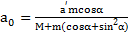Ответ: , , .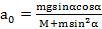

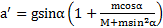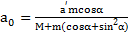Пример 8. Найти в примере 7 смещение наклонной плоскости по горизонтали после того как тело опустится на высоту h. Чему будут равны скорости тела и наклонной плоскости в этот момент времени?

Дано: 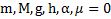.Найти: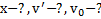

Решение:Путь, проходимый телом вдоль наклонной плоскости за время t, и смещение плоскости за это время описываются уравнениям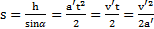и и 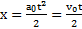. Откуда с учетом примера 7 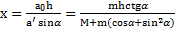. Скорость тела 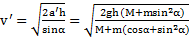, а наклонной плоскости ― .

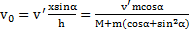Ответ: , , .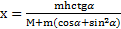

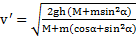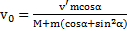Пример 9. Решить задачу в примере 7 в предположении, что между телом и наклонной плоскостью действуют силы трения. Коэффициент трения между телом и плоскостью равен μ.

Дано: 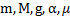.Найти: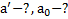

Решение:Согласно примеру 7 силы трения (рис.33), действующие между телом и плоскостью равны

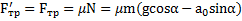
Второй закон Ньютона для наклонной плоскости в направлении оси Xбудет иметь вид:

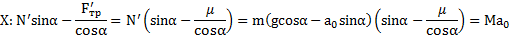
Откуда ускорение наклонной плоскости

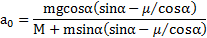
Второй закон Ньютона для тела в проекциях на ось 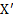движущейся СОбудет иметь вид:

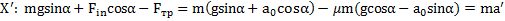
Откуда ускорение тела относительно наклонной плоскости

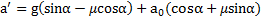
Ответ: 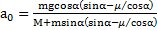, .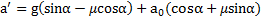