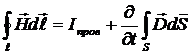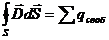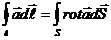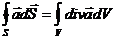Система уравнений Максвелла в интегральной и дифференциальной формах. Электромагнитное поле.
В законе электромагнитной индукции (ЭМИ) ℇ 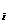 = -dФ/dt ЭДС можно представить по определению как циркуляцию поля сторонних сил
= -dФ/dt ЭДС можно представить по определению как циркуляцию поля сторонних сил
ℇ = 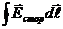 (см. часть 2, лекция №20), в данном случае (ЭМИ) сторонние силы не связаны ни с химическими, ни с тепловыми процессами, они также не могут быть магнитными силами, по тому, что такие силы работу над зарядами не совершают. Остается заключить, что индукционный ток обусловлен возникающим в проводе электрическим полем, тогда ЭДС
(см. часть 2, лекция №20), в данном случае (ЭМИ) сторонние силы не связаны ни с химическими, ни с тепловыми процессами, они также не могут быть магнитными силами, по тому, что такие силы работу над зарядами не совершают. Остается заключить, что индукционный ток обусловлен возникающим в проводе электрическим полем, тогда ЭДС
|
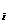 =
= 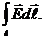 Магнитный поток по определению Ф =
Магнитный поток по определению Ф = 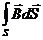 . Подставляя в закон ЭМИ получим
. Подставляя в закон ЭМИ получим (30-4)
Это первое уравнение Максвелла.

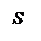
 Интеграл в правой части берется по произвольной поверхности S, опирающейся на контур ℓ (рис. 30.3).
Интеграл в правой части берется по произвольной поверхности S, опирающейся на контур ℓ (рис. 30.3).
 (Поскольку в общем случае
(Поскольку в общем случае 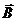 может быть
может быть
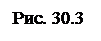

 функцией и координат, то берем частную
функцией и координат, то берем частную
производную 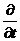 )
)
Смысл первого уравнения соответствует
максвелловской трактовке явления ЭМИ, то
есть, изменяющееся со временем магнитное поле порождает вихревое электрическое поле.
Второе уравнение Максвелла
|
(30-5)
Это уравнение выражает тот факт, что силовые линии магнитного поля не имеют источника (нет «магнитных зарядов») и всегда замкнуты и, что оно имеет вихревой характер, поток вектора магнитной индукции равен нулю.
Третье уравнение Максвелла
|
(30-6)
Это обобщенный закон полного тока (см. часть 3, лекция №24), который подчеркивает тот факт, что магнитное поле может создаваться не только токами проводимости ( 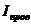 ), но и перемещенным электрическим полем («ток смещения»
), но и перемещенным электрическим полем («ток смещения» 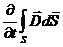 ).
).
Четвертая теорема Максвелла (см. часть 3, лекция №18).
|
(30-7)
Физически эта теорема подчеркивает тот факт, что электрическое поле может создаваться зарядами, то есть источниками силовых линий электрического поля являются электрические заряды.
Уравнения (30-3,5,6,7) представляют уравнения Максвелла в интегральной форме.
Уравнения Максвелла подчеркивают тот факт, что электрическое поле может создаваться как зарядами, так и переменным магнитным полем, а магнитное поле может создаваться как токами проводимости, так и переменным электрическим полем. При этом магнитное поле всегда носит вихревой характер, о чем говорит второе уравнение Максвелла. Электрическое поле, создаваемое зарядами и переменным магнитным полем носят различный характер.Силовые линии в первом случае начинаются и кончаются на зарядах (четвертое уравнение Максвелла). А электрическое поле, создаваемое переменным магнитным полем не имеет источников и носит вихревой характер, также как магнитное поле (первое уравнение Максвелла).
В вакууме, где нет зарядов и токов, магнитное поле может создаваться только переменным электрическим полем, а электрическое поле только переменным магнитным полем.
Эту совокупность непрерывно изменяющихся и порождающих друг друга электрического и магнитного полей Максвелл назвал электромагнитным полем.
Кроме четырех рассмотренных уравнений в полную систему уравнений Максвелла входят еще три уравнения, называемых материальными. В них входят характеристики вещества («материи»), такие как диэлектрическая и магнитная проницаемости ℰ и µ, проводимость σ.
|
Связь 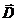 и
и 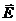 (лекция №18, часть 3)
(лекция №18, часть 3)
|
Связь 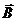 и
и 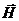 (лекция №23, часть 3)
(лекция №23, часть 3)
|
Закон Ома в локальной форме (лекция №20, часть 3)
Уравнения Максвелла (30-4) ÷ (30-7) можно представить в дифференциальной форме, т.е. в виде системы дифференциальных уравнений. Для этого используем теоремы Стокса
|
(30-8)
и Остроградского – Гаусса:
|
где 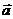 - некоторый вектор в нашем случае:
- некоторый вектор в нашем случае: 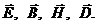 (О функции rot
(О функции rot 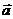 см. примечание к п.2).
см. примечание к п.2).
Первое уравнение Максвелла
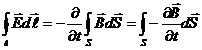
С другой стороны, используя теорему Стокса, получим
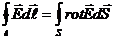
Поскольку равны левые части, равны и правые
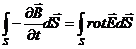
откуда следует
|
(30-10)
Второе уравнение Максвелла
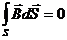
С другой стороны из теоремы Остроградского – Гаусса
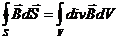
|
Третье уравнение запишем, предварительно выразив токи проводимости через плотность токов проводимости 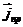
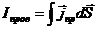 ,
,
тогда
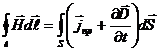
с другой стороны
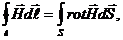
получим
|
(30-12)
Аналогичный подход для четвертого уравнения дает систему уравнений
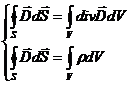 ,
,
|
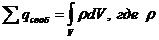 - объемная плотность заряда) из которой следует:
- объемная плотность заряда) из которой следует: (30-13)
Сведем четыре уравнения Максвелла в интегральной и дифференциальной формах, а также три материальных уравнения в таблицу:
Уравнения Максвелла
| Интегральная форма | Дифференциальная форма |
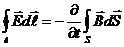 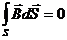 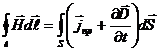 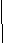 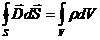 | 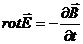 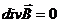 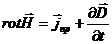 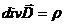  |
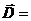 ℰℰ
ℰℰ 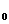
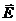 ;
; 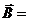 μμ
μμ 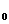
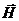 ;
; 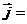 σ
σ 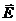
Отметим, что физический смысл уравнений в дифференциальной форме такой же, что и соответствующих уравнений в интегральной форме. Интегрируя их, можно получить 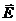 ,
, 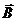 ,
, 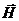 ,
, 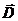 .
.
Примечание.Вихревое электрическое поле характеризуется особой векторной величиной, называемой ротором напряженности поля: 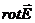 . Вектор ротора приложен в центре поля перпендикулярно плоскости его силовых линий (в случае круговых линий – в центре окружностей) и направлен относительно них согласно правилу правого винта.
. Вектор ротора приложен в центре поля перпендикулярно плоскости его силовых линий (в случае круговых линий – в центре окружностей) и направлен относительно них согласно правилу правого винта.
По определению
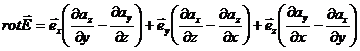 .
.
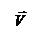






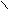

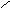
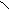


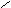

 Наглядное представление о роторе вектора можно получить, представив себе небольшую легкую турбинку, помещенную в данную точку текущей жидкости.
Наглядное представление о роторе вектора можно получить, представив себе небольшую легкую турбинку, помещенную в данную точку текущей жидкости.


 |
3. Волновые уравнения для электромагнитного поля и их решения. Скорость распространения электромагнитных волн в средах. Основные свойства электромагнитных волн.
Пусть имеется однородная и изотропная среда вдали от зарядов и токов. Возбудим в какой-либо точке пространства переменное электрическое гармоническое поле 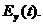 (Предположим
(Предположим 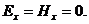 Для простоты рассматриваем этот частный случай).
Для простоты рассматриваем этот частный случай).
Из уравнений Максвелла при условии сделанных предположений можно получить волновые уравнения электромагнитного поля



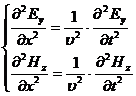 , (30-14)
, (30-14)
где - скорость распространения электро-
магнитной волны.
Процесс распространения электромагнитного поля в пространстве называется электромагнитной волной.
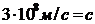 Подставим ℰ
Подставим ℰ 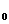 = 8,85
= 8,85 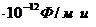 μ
μ  =
= 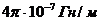 в выражение для скорости u. Если среда – вакуум, то ℰ = 1, μ = 1, тогда получим u = ,то есть скорость электромагнитной волны в вакууме равна скорости света в вакууме. Это обстоятельство приводит к выводу, что свет - электромагнитная волна.
в выражение для скорости u. Если среда – вакуум, то ℰ = 1, μ = 1, тогда получим u = ,то есть скорость электромагнитной волны в вакууме равна скорости света в вакууме. Это обстоятельство приводит к выводу, что свет - электромагнитная волна.
Решения уравнений (30-14)
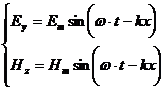 (30-15)
(30-15)
Выражения (30-15) – уравнения электромагнитной волны. Их графическое



Как показывает опыт, электромагнитные волны проходят через диэлектрики и отражаются от металлов. Для них свойственны такие явления как интерференция, дифракция, поляризация, дисперсия (рассмотрим далее в разделе «Оптика»).
Итак, из решения уравнений Максвелла получаются следующие выводы:
– если в какой-либо ограниченной области пространства возникает электромагнитное поле, то оно не остается локализованным в этой области, а распространяется с конечной скоростью, зависящей от свойств среды;
– если электрическое и магнитные поля меняются по простому гармоническому закону, то электромагнитное поле распространяется в пространстве в виде плоской электромагнитной волны.