Интегральное исчисление функций одной переменной.
Интегральное исчисление функций одной переменной.
Понятие неопределенного интеграла
Определение 3.5.1. Функция F(x) называется первообразной функцией для данной функции f(x) на данном промежутке, если на этом промежутке 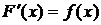 .
.
Теорема 3.5.1. Если F1(x) и F2(x) – две первообразные для функции f(x) на некотором промежутке, то разность между ними на этом промежутке равна постоянному числу.
Определение 3.5.2.Выражение F(x)+С, где F(x) – первообразная функции f(x) и С – произвольная постоянная, называется неопределенным интегралом от функции f(x) и обозначается символом 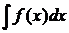 , причем f(x) называется подынтегральной функцией,
, причем f(x) называется подынтегральной функцией, 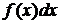 – подынтегральным выражением, x – переменной интегрирования;
– подынтегральным выражением, x – переменной интегрирования; 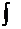 – знак неопределенного интеграла.
– знак неопределенного интеграла.
Таким образом, по определению 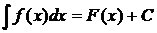 , если
, если 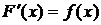 .
.
Теорема 3.5.2. Если функция f(x) непрерывна на отрезке [a; b], то на этом отрезке у функции f(x) существует первообразная.
Свойства неопределенного интеграла
1. 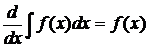 или
или 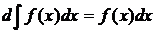 .
.
2. 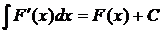 или
или 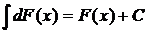 .
.
3. Постоянный множитель можно выносить за знак интеграла:
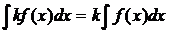 .
.
4. Интеграл от суммы двух функций равен сумме интегралов от этих функций:
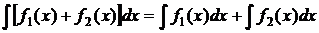 .
.
Таблица основных интегралов
1. 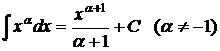 ; ; | 5. 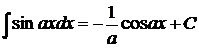 ; ; | ||
2. 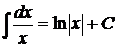 ; ; | 6. 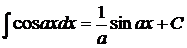 ; ; | ||
3. 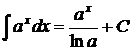 ; ; | 7. 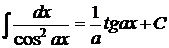 ; ; | ||
4. 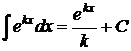 ; ; | 8. 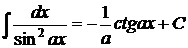 ; ; | ||
9. 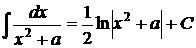 ; ; | |||
10. 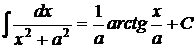 ; ; | |||
11. 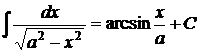 ; ; | |||
12. 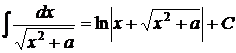 ; ; | |||
13. 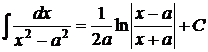 . . | |||
Пример 3.5.1. Приведем примеры непосредственного интегрирования.
1. 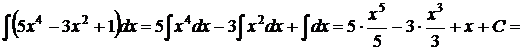
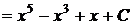 .
.
2. 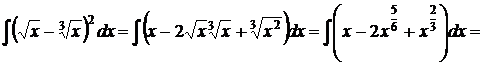
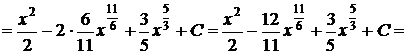
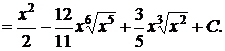
Основные методы интегрирования
Замена переменной интегрирования
Делая подстановку х=φ(t), где φ(t) – функция, имеющая непрерывную производную, получим 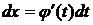 и
и
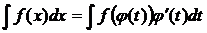 – формула замены переменной в неопределенном интеграле.
– формула замены переменной в неопределенном интеграле.
Пример 3.5.2. 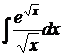 найдем подстановкой х=t2. Тогда dx=2tdt и
найдем подстановкой х=t2. Тогда dx=2tdt и 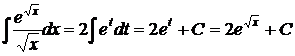 .
.
Иногда вместо подстановки х=φ(t) лучше выполнить замену переменной вида t=ψ(x).
Пример 3.5.3. Найти 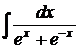 .
.
○ Полагая 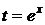 , получаем:
, получаем: 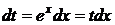 ,
, 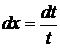
и
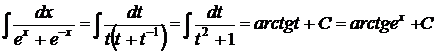 .●
.●
Интегрирование по частям
Пусть u=u(x) и v=v(x) – непрерывно дифференцируемые функции, тогда 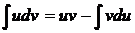 – формула интегрирования по частям (произвольная постоянная интегрирования С здесь включена в слагаемое
– формула интегрирования по частям (произвольная постоянная интегрирования С здесь включена в слагаемое 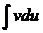 ).
).
Пример 3.5.4. Найти 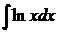 .
.
○ 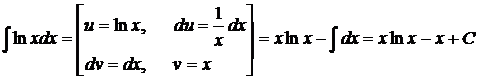 .●
.●
Пример 3.5.5. Найти 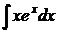 .
.
○ 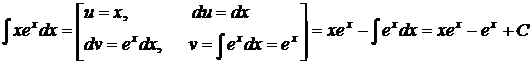 .●
.●
Примечание. Иногда бывает необходимо повторное интегрирование по частям.
Пример 3.5.6. Найти 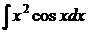 .
.
○
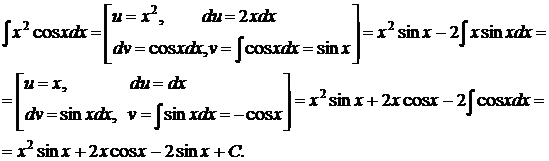 ●
●
Отметим три основных класса функций, интегралы от которых берутся по частям:
| I | 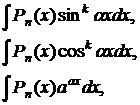 где где 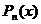 – многочлен n-ой степени, n,k,αÎN – многочлен n-ой степени, n,k,αÎN | 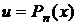 | Интегрирование по частям применять n раз. |
| II | 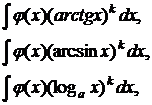 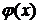 – рациональная или иррациональная функция, в частности, – рациональная или иррациональная функция, в частности, 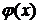 º1. º1. | 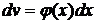 | Интегрирование по частям применять k раз. |
| III |  | u – любая из функций 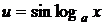 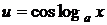 | Применяя двукратное интегрирование по частям получим линейное уравнение, относительно искомого интеграла. Из этого уравнения и находится данный интеграл. |
Замена переменной в определенном интеграле
Формула замены переменной в определенном интеграле:
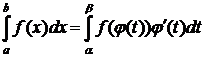 ,
,
где 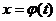 , α и β определяются из условий
, α и β определяются из условий 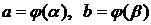 соответственно.
соответственно.
Пример 3.5.12. Вычислить 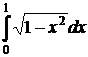 .
.
○
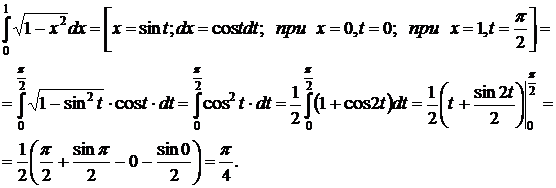
●
Теорема 3.5.6. (Теорема о среднем)Если функция f(x) непрерывна на отрезке [a; b], то в интервале (a; b) найдется такая точка с, что
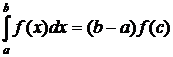 .
.
Интегрирование по частям в определенном интеграле
Пусть u=u(x), v=v(x) – непрерывно дифференцируемые на отрезке [a; b] функции. Тогда
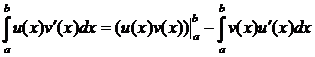 .
.
Несобственные интегралы
Интегралы с одним или обоими бесконечными пределами получили название несобственных интегралов первого рода. Здесь также, как при вычислении определенных интегралов, можно на практике использовать формулу Ньютона-Лейбница, однако следует помнить, что символ ∞ – не число, а условное обозначение неограниченного возрастания (или убывания) аргумента в процессе его изменения. То есть, со строгих позиций, вычисление несобственного интеграла первого рода – это вычисление некоторого предела, с постоянным использованием теорем о бесконечно малых и бесконечно больших величинах.
Таким образом:
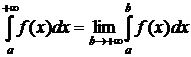 ;
;
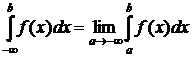 ;
;
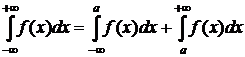 .
.
То есть, символы бесконечности условно заменяются буквенными параметрами, применяется формула Ньютона-Лейбница, после чего обычным образом вычисляются указанные пределы. Если в результате такого расчета получится конечное число А (включая 0), то ответ следует записать в форме: интеграл сходится к значению А. Если же результатом будет +∞ (или –∞) или предел не существует, то ответ: интеграл расходится.
В практических вычислениях, вполне допустимо не использовать в явной форме операторы lim, но не следует забывать о том, что на самом деле вычисляются пределы, а не конкретные числовые значения.
Следующим видом несобственных интегралов являются интегралы от функций с разрывом на одном конце (или обоих концах) интервала интегрирования или с разрывом внутри интервала интегрирования. Например: 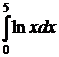 ,
, 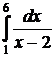 и т.п. Такие интегралы носят название несобственных интегралов второго рода. Эти интегралы очень опасны, т.к. часто выглядят вполне безобидно (по невнимательности забываем особые точки подынтегральной функции), но применение формулы Ньютона-Лейбница приводит к неверным результатам.
и т.п. Такие интегралы носят название несобственных интегралов второго рода. Эти интегралы очень опасны, т.к. часто выглядят вполне безобидно (по невнимательности забываем особые точки подынтегральной функции), но применение формулы Ньютона-Лейбница приводит к неверным результатам.
Вычисление несобственных интегралов второго рода осуществляется приведением к интегралам первого рода (или сумме таких интегралов), то есть, ставится задача вычисления предела относительно точки, в которой подынтегральная функция разрывна.
Интегральное исчисление функций одной переменной.
