Образец возможного решения задачи №5
Образец радия 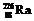 массой
массой 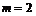 г находится в свинцовой оболочке, не проницаемой для
г находится в свинцовой оболочке, не проницаемой для  -частиц. Период полураспада радия равен
-частиц. Период полураспада радия равен 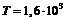 лет, а масса и средняя скорость
лет, а масса и средняя скорость  -частиц равны
-частиц равны 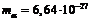 кг и
кг и 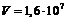 м/с, соответственно. Учитывая отдачу, получаемую ядрами при распаде, найти количество теплоты Q, которое выделится в образце и оболочке за время
м/с, соответственно. Учитывая отдачу, получаемую ядрами при распаде, найти количество теплоты Q, которое выделится в образце и оболочке за время 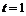 мин?
мин?
За время t распадётся
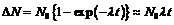 (15)
(15)
ядер радия, где  – постоянная распада. Первоначальное количество ядер радия
– постоянная распада. Первоначальное количество ядер радия 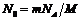 , где
, где 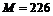 г/моль – масса моля радия. Количество теплоты
г/моль – масса моля радия. Количество теплоты 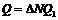 , где
, где 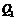 - количество энергии, выделяющейся при одном распаде:
- количество энергии, выделяющейся при одном распаде:
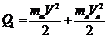 . (16)
. (16)
Скорость ядра 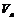 после распада находим из закона сохранения импульса
после распада находим из закона сохранения импульса
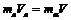 . (17)
. (17)
Подставляя 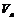 в формулу для
в формулу для 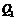 , находим затем
, находим затем
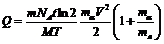 =3,7 Дж.
=3,7 Дж.
ВСО-15
1. Скорость тела массы m в вязкой жидкости убывает с пройденным расстоянием l по закону v = v0 - bl, где v0 — начальная скорость, а b>0 — постоянный коэффициент. Как зависит сила вязкого трения, действующая на тело со стороны жидкости, от скорости тела? Действие других сил не учитывать.
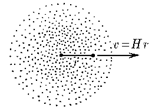
- Скорость пылинок однородного шарового облака направлена радиально и пропорциональна расстоянию до центра: v = Hr; это относится к начальному моменту. При какой наибольшей начальной плотности облако будет неограниченно расширяться?
- Требуется перевести некоторое количество вещества изопропилена из состояния 1 с температурой
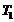 в состояние 2 с температурой
в состояние 2 с температурой 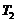 (
( 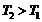 ) таким образом, чтобы температура в течение всего обратимого процесса 1–2 не убывала, а тепло не отводилось от вещества. Минимальное количество теплоты, которое может быть передано в этом процессе, равно
) таким образом, чтобы температура в течение всего обратимого процесса 1–2 не убывала, а тепло не отводилось от вещества. Минимальное количество теплоты, которое может быть передано в этом процессе, равно 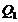 . Какое максимальное количество теплоты
. Какое максимальное количество теплоты 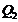 может быть передано в этом процессе при заданных условиях?
может быть передано в этом процессе при заданных условиях?
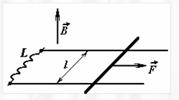
- На двух проводящих горизонтальных параллельных рельсах, находящихся на расстоянии l друг от друга, перпендикулярно рельсам расположена проводящая перемычка массы m, которая может скользить по рельсам без трения. Вся система помещена в однородное вертикальное магнитное поле индукции B. Рельсы соединили с помощью катушки индуктивностью L , а к перемычке приложили постоянную горизонтально направленную силу F. Пренебрегая сопротивлением перемычки и рельсов определите характер движения перемычки в этом случае.
- Точечный заряд q помещают на расстоянии
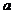 от центра незаряженного проводящего шара радиуса
от центра незаряженного проводящего шара радиуса 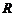 . Найти силу, с которой точечный заряд q притягивает шар.
. Найти силу, с которой точечный заряд q притягивает шар.
РЕШЕНИЕ
варианта №1
| Образец возможного решения задачи №1 | |
1. По 2-ому закону Ньютона: 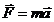 , где ускорение материальной точки (м.т.) , где ускорение материальной точки (м.т.) 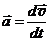 . 2. Полагая наше тело м.т. запишем для него 2-ой закон Ньютона в проекции на касательное (тангенциальное) направление . 2. Полагая наше тело м.т. запишем для него 2-ой закон Ньютона в проекции на касательное (тангенциальное) направление 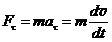 (1) 3. Подставив заданную зависимость v (l)= v0 - bl, и используя правило вычисления производной сложной функции, получим: (1) 3. Подставив заданную зависимость v (l)= v0 - bl, и используя правило вычисления производной сложной функции, получим: 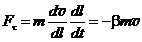 . (2) Из уравнения (2) делаем вывод о том, сила сопротивления . (2) Из уравнения (2) делаем вывод о том, сила сопротивления 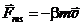 . Ответ: . Ответ: 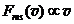 . . | |
| Критерии оценки выполнения задания | Баллы |
Приведено полное правильное решение, включающее следующие элементы: I) записаны положения теории и физические законы, закономерности; применение которых необходимо для решения задачи выбранным способом (в данном случае: 2-ой закон Ньютона, определение тангенциального ускорения - п.1); II) описаны все вновь вводимые в решении буквенные обозначения физических величин (за исключением обозначений констант, и обозначений, используемых в условии задачи) п.2; III) проведены необходимые математические преобразования и расчёты, приводящие к правильному ответу (п.3 формула (2)), IV) представлен правильный ответ (в данном случае – зависимость 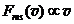 , допустим ответ , допустим ответ 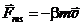 ) Комментарий экспертам:задача проста для олимпиадной, поэтому любые предположения, напрямую не следующие из условия задачи, должны считаться не обоснованными (например, о прямолинейности движения). ) Комментарий экспертам:задача проста для олимпиадной, поэтому любые предположения, напрямую не следующие из условия задачи, должны считаться не обоснованными (например, о прямолинейности движения). |
| Образец возможного решения задачи №2 | |
1. 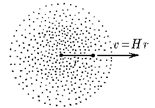 Рассмотрим движение пылинки массой Рассмотрим движение пылинки массой 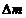 , находящегося на расстоянии , находящегося на расстоянии 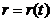 от центра при расширении облака. По 2-ому закону Ньютона: от центра при расширении облака. По 2-ому закону Ньютона: 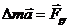 , (1) где ускорение пылинки (м.т.) , (1) где ускорение пылинки (м.т.) 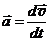 . По закону всемирного тяготения: . По закону всемирного тяготения: 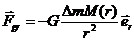 . (2) 2. Предполагая движение радиальным, запишем для массы . (2) 2. Предполагая движение радиальным, запишем для массы 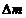 2-ой закон Ньютона в проекции на радиальное направление 2-ой закон Ньютона в проекции на радиальное направление 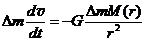 (3) 3. Заметив, что при радиальном движении скорость точек среды (3) 3. Заметив, что при радиальном движении скорость точек среды 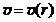 , а масса шара радиусом , а масса шара радиусом 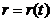 остается постоянной остается постоянной 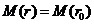 , где , где 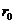 – радиальная координата пылинки в начальный момент времени. Используя правило вычисления производной сложной функции, получим: – радиальная координата пылинки в начальный момент времени. Используя правило вычисления производной сложной функции, получим: 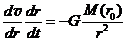 . (4) Учитывая, что . (4) Учитывая, что 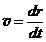 , проинтегрируем уравнение (4): , проинтегрируем уравнение (4): 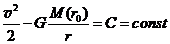 . (5) 4. Облако пыли будет неограниченно расширятся, если . (5) 4. Облако пыли будет неограниченно расширятся, если 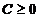 . В начальный момент времени: . В начальный момент времени: 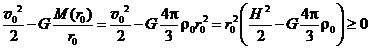 . (6) Из уравнения (6) делаем вывод о том, облако будет неограниченно расширяться при наибольшей начальной плотности . (6) Из уравнения (6) делаем вывод о том, облако будет неограниченно расширяться при наибольшей начальной плотности 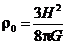 . Ответ: . Ответ: 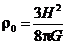 . . | |
| Критерии оценки выполнения задания | Баллы |
Приведено полное правильное решение, включающее следующие элементы: I) записаны положения теории и физические законы, закономерности; применение которых необходимо для решения задачи выбранным способом (в данном случае: 2-ой закон Ньютона, сила тяготения, действующая на пылинку - п.1); II) описаны все вновь вводимые в решении буквенные обозначения физических величин (за исключением обозначений констант, и обозначений, используемых в условии задачи) п. 1-2; III) проведены необходимые математические преобразования и расчёты, приводящие к правильному ответу (п.3-4 формулы(4-6)), IV) представлен правильный ответ (в данном случае – 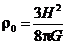 ,) Комментарий экспертам:задача имеет простое решение в виде уравнения Бернулли для идеальной жидкости с нулевым давлением, но в этом случае д.б. приведен его вывод. ,) Комментарий экспертам:задача имеет простое решение в виде уравнения Бернулли для идеальной жидкости с нулевым давлением, но в этом случае д.б. приведен его вывод. |
| Образец возможного решения задачи №3 | |
1. 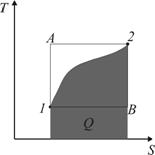 Проще всего данную задачу решать использую Проще всего данную задачу решать использую 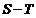 диаграмму процесса. В соответствии с условием задачи, количество теплоты, которое может быть передано в процессе 1–2: диаграмму процесса. В соответствии с условием задачи, количество теплоты, которое может быть передано в процессе 1–2: 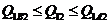 , 2. Следовательно минимальное количество теплоты при переходе вещества из состояния 1 в состояние 2 может быть передано в процессе 1–B–2 и равно , 2. Следовательно минимальное количество теплоты при переходе вещества из состояния 1 в состояние 2 может быть передано в процессе 1–B–2 и равно 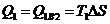 , (2) а максимальное количество теплоты при переходе вещества из состояния 1 в состояние 2 может быть передано в процессе 1–A–2 и равно , (2) а максимальное количество теплоты при переходе вещества из состояния 1 в состояние 2 может быть передано в процессе 1–A–2 и равно 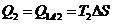 . (3) где . (3) где 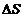 – приращение энтропии. Из (2) и (3) получим – приращение энтропии. Из (2) и (3) получим 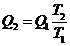 Ответ: Ответ: 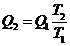 . . | |
| Критерии оценки выполнения задания | Баллы |
Приведено полное правильное решение, включающее следующие элементы: I) записаны положения теории и физические законы, закономерности; применение которых необходимо для решения задачи выбранным способом (в данном случае: графически показано, что количество теплоты при переходе вещества из состояния 1 в состояние 2 ограничено сверху и снизу, графически найдено количество теплоты - п.1-2); II) описаны все вновь вводимые в решении буквенные обозначения физических величин (за исключением обозначений констант, и обозначений, используемых в условии задачи) п. 1-2; III) проведены необходимые математические преобразования и расчёты, приводящие к правильному ответу, IV) представлен правильный ответ (в данном случае – 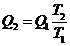 ,) Комментарий экспертам:задача может быть решена с использованием теоремы Карно. Упрощением задачи следует считать применение модели идеального газа к данному веществу. ,) Комментарий экспертам:задача может быть решена с использованием теоремы Карно. Упрощением задачи следует считать применение модели идеального газа к данному веществу. |
| Образец возможного решения задачи №4 | |
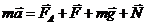 , (1) , (1) 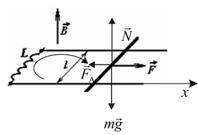 В проекции на ось В проекции на ось 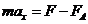 , (2) где сила Ампера: , (2) где сила Ампера: 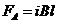 , (3) , (3) 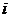 – сила тока в проводниках, положительное направление которого показано на рис. – сила тока в проводниках, положительное направление которого показано на рис.
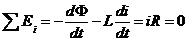 , (4) т.к. по условию задачи можно пренебречь сопротивлением проводников. , (4) т.к. по условию задачи можно пренебречь сопротивлением проводников.
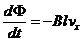 . (5) . (5)
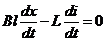 (6) Интегрируя (6), получим (6) Интегрируя (6), получим 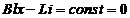 (из начальных условий) (6) (из начальных условий) (6)
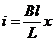 и силу Ампера и силу Ампера 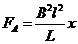 , (7) , (7)
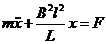 (8) или (8) или 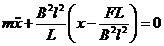 – это диф. ур-ние гармонических колебаний. – это диф. ур-ние гармонических колебаний.
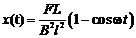 , где циклическая частота , где циклическая частота 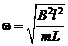 Ответ: Ответ: 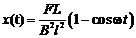 , где циклическая частота , где циклическая частота 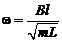 . . | |
| Критерии оценки выполнения задания | Баллы |
Приведено полное правильное решение, включающее следующие элементы: I) записаны положения теории и физические законы, закономерности; применение которых необходимо для решения задачи выбранным способом (в данном случае: 2-ой закон Ньютона, сила Ампера, явление электромагнитной индукции (ЭМИ) и самоиндукции - пп.1–5); II) описаны все вновь вводимые в решении буквенные обозначения физических величин (за исключением обозначений констант, и обозначений, используемых в условии задачи) пп. 1-5; III) проведены необходимые математические преобразования и расчёты, приводящие к правильному ответу пп.6–7, IV) представлен правильный ответ (в данном случае – 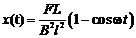 , где циклическая частота , где циклическая частота 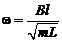 .,) .,) |
| Образец возможного решения задачи №5 | |
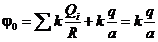 , (1) так как , (1) так как 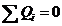 . . 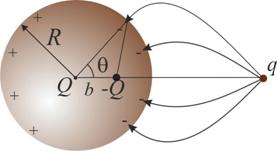 В соответствии с методом изображений разместим заряды: В соответствии с методом изображений разместим заряды: 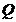 в центре, а в центре, а 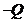 на расстоянии на расстоянии 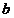 от центра. Тогда потенциал на поверхности сферы от центра. Тогда потенциал на поверхности сферы 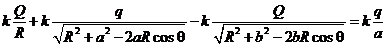 , (2) , (2)
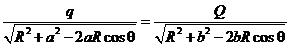 , (3) После не сложных алгебраических преобразований, получим , (3) После не сложных алгебраических преобразований, получим 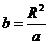 . (4) . (4) 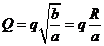 . (5) . (5)
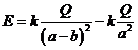 (6) и направлена к центру шара. (6) и направлена к центру шара.
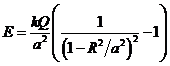 (7) Следовательно, сила, действующая на точечный заряд (7) Следовательно, сила, действующая на точечный заряд 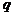 , равна , равна 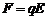 и с учетом (7) и 3-его закона Ньютона и с учетом (7) и 3-его закона Ньютона 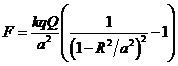 Ответ: Ответ: 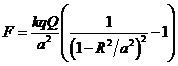 ,. ,. | |
| Критерии оценки выполнения задания | Баллы |
Приведено полное правильное решение, включающее следующие элементы: I) записаны положения теории и физические законы, закономерности; применение которых необходимо для решения задачи выбранным способом (в данном случае: 3-ий закон Ньютона, принцип суперпозиции электрических полей, метод изображений, - пп.1,3,4); II) описаны все вновь вводимые в решении буквенные обозначения физических величин (за исключением обозначений констант, и обозначений, используемых в условии задачи) пп. 1-4; III) проведены необходимые математические преобразования и расчёты, приводящие к правильному ответу пп.2–4, IV) представлен правильный ответ (в данном случае – 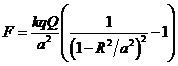 .) .) |

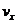
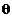 при условии:
при условии: