Образец возможного решения задачи №2
ДЕМОВЕРСИЯ ВАРИАНТОВ ВСО
ВСО-13
- Вертикально расположенный диск радиуса r катится без проскальзывания по горизонтальной поверхности. Три точки А, В и С отмечены на ободе диска таким образом, что дуги АВ и ВС равны a (0<a<p/2). Найти величину угловой скорости диска в тот момент, когда сумма расстояний точек А, В и С до горизонтальной поверхности минимальна, считая скорость точки А в этот момент известной и равной v.
- Ракета массы m0 = 1 т с поперечным сечением S = 5 м2 летела с выключенным двигателем и попала в облако пыли. Масса каждой пылинки m1 = 10-6 кг, их концентрация n =10-4 м-3, а соударения с ракетой абсолютно неупругие. Какова длина облака l, если после пролета через него ракета потеряла 1% скорости?
- Между двумя плоскостями с постоянными температурами T1 и T2 (T1 > T2) находится идеальный газ с молярной массой M. Расстояние между плоскостями равно H. К верхней плоскости на невесомой пружине подвешен маленький шарик массой m, средняя плотность которого равна r0. Длина пружины в недеформированном состоянии L0. Коэффициент жёсткости пружины равен k. Температура линейно возрастает при удалении от нижней плоскости. Найдите давление в газе p, если в положении равновесия длина пружины равна её длине в недеформированном состоянии L0 .
- Три одинаковых изолированных металлических шара расположены в вершинах равностороннего треугольника. Проволочкой, подключенной к удаленному заряженному проводнику, потенциал которого неизвестен, но поддерживается постоянным, по очереди касаются каждого из шаров. Заряды на первых двух шарах оказались после этого равными q1и q2. Найти заряд q3 на третьем шаре.
- Определить энергию кулоновского расталкивания протонов в ядре с массовым числом A в предположении, что протоны распределены по ядру равномерно. Число протонов в ядре Z. Указание: радиус ядра
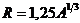 10-15 м.
10-15 м.
Решение задач
Задача №1
Определим положение точек А,В и С в заданный момент времени. Для этого мысленно поместим в эти точки одинаковые массы. Тогда сумма расстояний от точек А,В и С до поверхности пропорциональна потенциальной энергии системы трех точечных масс. Очевидно, минимум потенциальной энергии достигается, когда центр масс системы занимает наинизшее положение, что происходит, когда точка В касается поверхности.
Так, как скорость точки А равна v, длина отрезка ВА равна 2rsin(α/2),а точка В является мгновенным центром скоростей, величина угловой скорости диска 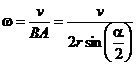
Ответ: 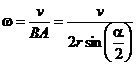
Задача №2

Задача №3

Задача № 4
Указание. Решение. Потенциалы проводников являются линейными однородными функциями их зарядов: 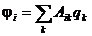 В силу симметрии все коэффициенты Aik с одинаковыми индексами равны
В силу симметрии все коэффициенты Aik с одинаковыми индексами равны
между собой. Точно так же равны все коэффициенты с разными индексами. Обозначая эти коэффициенты через А и В соответственно, можем написать j1=Aq1+ B(q2 + q3) и аналогично для остальных проводников. При зарядке первого шара он получает потенциал j1=Aq1. При зарядке остальных двух шаров потенциал первого шара меняется, но его значения для решения не нужны. При зарядке второго шара его потенциал становится равным такжеj1 = Aq2 + Bq1. Аналогично, для третьего шара j1 = Aq3 + B(q1 + q2). Таким образом, Aq1 = Aq2 + Bq1 = Aq3 + B(q1 + + q2).
Ответ: 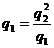
Решение задачи №5
Энергия кулоновского взаимодействия определяется так:
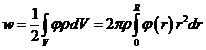 .
.
Плотность зарядов в шаре определим так:
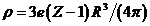 ,
,
Тогда при 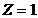 энергия взаимодействия равна нулю.
энергия взаимодействия равна нулю.
Напряжённость электрического поля равномерно заряженного шара зависит от расстояния r до его центра:
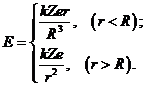
Интегрируя данное соотношение по радиусу от r 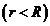 до бесконечности, находим потенциал
до бесконечности, находим потенциал
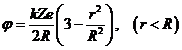 .
.
Подставляя потенциал в верхнюю формулу и интегрируя, получаем
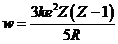 .
.
Наконец, подставляя радиус ядра и элементарный заряд, получаем
Ответ: 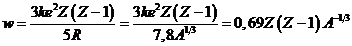 , эрг
, эрг
ВСО-14
1. Верхний конец однородного стержня массой M и длиной L шарнирно закреплён. Маленький шарик массой m подвешен на нити длиной L в точке крепления стержня. От вертикально расположенного и находящегося в покое стержня шарик отводят в сторону так, что он поднимается на высоту h относительно нижнего положения, и отпускают. На какую высоту поднимутся шарик и конец стержня после неупругого удара? Как изменится ответ, если отклонить и отпустить с той же высоты конец стержня, а не шарик?
2. Волк преследует зайца, который удирает от него к норе с постоянной скоростью u . Скорость волка 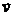 постоянна по величине направлена все время на зайца, причем v>u, В начальный момент
постоянна по величине направлена все время на зайца, причем v>u, В начальный момент 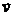 ^
^ 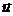 , расстояние между волком и зайцем равно L, а расстояние от зайца до норы равно b . Найти время погони t и наибольшее начальное расстояние Lмакс., при котором волк догонит зайца.
, расстояние между волком и зайцем равно L, а расстояние от зайца до норы равно b . Найти время погони t и наибольшее начальное расстояние Lмакс., при котором волк догонит зайца.
3. 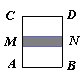 Боковые стенки цилиндра АС и BD, его крышка СD и поршень MN сделаны из материала, не проводящего тепло. Поршень MN может двигаться в цилиндре без трения. Сверху и снизу поршня находится по одному молю одного и того же идеального газа с молярной теплоемкостью при постоянном объеме
Боковые стенки цилиндра АС и BD, его крышка СD и поршень MN сделаны из материала, не проводящего тепло. Поршень MN может двигаться в цилиндре без трения. Сверху и снизу поршня находится по одному молю одного и того же идеального газа с молярной теплоемкостью при постоянном объеме 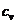 и показателем адиабаты
и показателем адиабаты 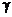 . Первый газ в нижней части цилиндра квазистатически нагревают, вследствие чего поршень MN перемещается. Выразить теплоемкость первого газа С1 при таком процессе через объемы газов V1 в верхней части и V2 в нижней части. Чему равна теплоемкость второго газа?
. Первый газ в нижней части цилиндра квазистатически нагревают, вследствие чего поршень MN перемещается. Выразить теплоемкость первого газа С1 при таком процессе через объемы газов V1 в верхней части и V2 в нижней части. Чему равна теплоемкость второго газа?
4. Образец радия 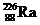 массой
массой 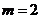 г находится в свинцовой оболочке, не проницаемой для
г находится в свинцовой оболочке, не проницаемой для 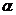 -частиц. Период полураспада радия равен
-частиц. Период полураспада радия равен 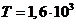 лет, а масса и средняя скорость
лет, а масса и средняя скорость 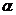 -частиц равны
-частиц равны 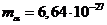 кг и
кг и 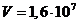 м/с, соответственно. Учитывая отдачу, получаемую ядрами при распаде, найти количество теплоты Q, которое выделится в образце и оболочке за время
м/с, соответственно. Учитывая отдачу, получаемую ядрами при распаде, найти количество теплоты Q, которое выделится в образце и оболочке за время 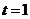 мин?
мин?
5. Однородная немагнитная сплошная среда содержит случайно распределенные включения в виде небольших одинаковых стальных шариков радиуса r с постоянной магнитной проницаемостью μ. Средняя концентрация шариков равна n. Расстояние между шариками намного больше их размеров, так, что влиянием шариков друг на друга можно пренебречь. Найдите среднюю по объему магнитную проницаемость среды.
РЕШЕНИЕ
Волк преследует зайца, который удирает от него к норе с постоянной скоростью u . Скорость волка 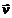 постоянна по величине и направлена все время на зайца, причем v>u, В начальный момент
постоянна по величине и направлена все время на зайца, причем v>u, В начальный момент  , расстояние между волком и зайцем равно L, а расстояние от зайца до норы равно b. Найти время погони t и наибольшее начальное расстояние Lмакс., при котором волк догонит зайца.
, расстояние между волком и зайцем равно L, а расстояние от зайца до норы равно b. Найти время погони t и наибольшее начальное расстояние Lмакс., при котором волк догонит зайца.
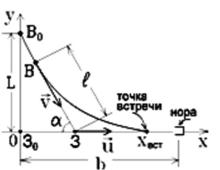
Рис.2. Пояснение к решению задачи №2.
Обозначим расстояние между участниками погони в произвольный момент времени через l (рис 2). За последующий бесконечно малый интервал времени dt волк сместится на расстояние vdt, заяц – на расстояние udt, а расстояние между нимистанет равным l + dl (рис.3). Стороны треугольника, изображенного на рисунке, связаны теоремой косинусов:
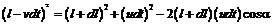
Раскрывая скобки пренебрегая слагаемыми второго порядка малости, находим:
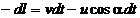
Интегрируя это уравнение с учетом начальных условий, получим:
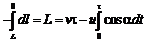 , (1)
, (1)
где в момент времени t = t происходит встреча и l = 0. С другой стороны, в момент встречи координаты участников должны быть одинаковыми, т.е.
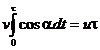 . (2)
. (2)
Исключив 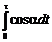 из уравнений (1) и (2), находим время погони t и координату точки встречи:
из уравнений (1) и (2), находим время погони t и координату точки встречи:
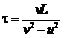 и
и 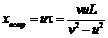
Так, как встреча состоится только если xвстр < b, то максимальное начальное расстояние между волком и зайцем, при котором охота будет успешной, равно:
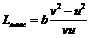
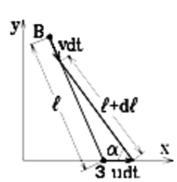
Рис.3. Перемещения волка и зайца за малый промежуток времени.
ВСО-15
1. Скорость тела массы m в вязкой жидкости убывает с пройденным расстоянием l по закону v = v0 - bl, где v0 — начальная скорость, а b>0 — постоянный коэффициент. Как зависит сила вязкого трения, действующая на тело со стороны жидкости, от скорости тела? Действие других сил не учитывать.
- Скорость пылинок однородного шарового облака направлена радиально и пропорциональна расстоянию до центра: v = Hr; это относится к начальному моменту. При какой наибольшей начальной плотности облако будет неограниченно расширяться?
- Требуется перевести некоторое количество вещества изопропилена из состояния 1 с температурой
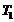 в состояние 2 с температурой
в состояние 2 с температурой 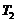 (
( 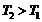 ) таким образом, чтобы температура в течение всего обратимого процесса 1–2 не убывала, а тепло не отводилось от вещества. Минимальное количество теплоты, которое может быть передано в этом процессе, равно
) таким образом, чтобы температура в течение всего обратимого процесса 1–2 не убывала, а тепло не отводилось от вещества. Минимальное количество теплоты, которое может быть передано в этом процессе, равно 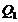 . Какое максимальное количество теплоты
. Какое максимальное количество теплоты 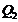 может быть передано в этом процессе при заданных условиях?
может быть передано в этом процессе при заданных условиях?
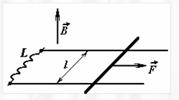
- На двух проводящих горизонтальных параллельных рельсах, находящихся на расстоянии l друг от друга, перпендикулярно рельсам расположена проводящая перемычка массы m, которая может скользить по рельсам без трения. Вся система помещена в однородное вертикальное магнитное поле индукции B. Рельсы соединили с помощью катушки индуктивностью L , а к перемычке приложили постоянную горизонтально направленную силу F. Пренебрегая сопротивлением перемычки и рельсов определите характер движения перемычки в этом случае.
- Точечный заряд q помещают на расстоянии
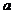 от центра незаряженного проводящего шара радиуса
от центра незаряженного проводящего шара радиуса 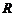 . Найти силу, с которой точечный заряд q притягивает шар.
. Найти силу, с которой точечный заряд q притягивает шар.
РЕШЕНИЕ
варианта №1
| Образец возможного решения задачи №1 | |
1. По 2-ому закону Ньютона: 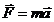 , где ускорение материальной точки (м.т.) , где ускорение материальной точки (м.т.) 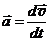 . 2. Полагая наше тело м.т. запишем для него 2-ой закон Ньютона в проекции на касательное (тангенциальное) направление . 2. Полагая наше тело м.т. запишем для него 2-ой закон Ньютона в проекции на касательное (тангенциальное) направление 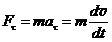 (1) 3. Подставив заданную зависимость v (l)= v0 - bl, и используя правило вычисления производной сложной функции, получим: (1) 3. Подставив заданную зависимость v (l)= v0 - bl, и используя правило вычисления производной сложной функции, получим: 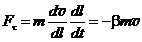 . (2) Из уравнения (2) делаем вывод о том, сила сопротивления . (2) Из уравнения (2) делаем вывод о том, сила сопротивления 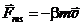 . Ответ: . Ответ: 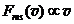 . . | |
| Критерии оценки выполнения задания | Баллы |
Приведено полное правильное решение, включающее следующие элементы: I) записаны положения теории и физические законы, закономерности; применение которых необходимо для решения задачи выбранным способом (в данном случае: 2-ой закон Ньютона, определение тангенциального ускорения - п.1); II) описаны все вновь вводимые в решении буквенные обозначения физических величин (за исключением обозначений констант, и обозначений, используемых в условии задачи) п.2; III) проведены необходимые математические преобразования и расчёты, приводящие к правильному ответу (п.3 формула (2)), IV) представлен правильный ответ (в данном случае – зависимость 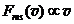 , допустим ответ , допустим ответ 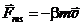 ) Комментарий экспертам:задача проста для олимпиадной, поэтому любые предположения, напрямую не следующие из условия задачи, должны считаться не обоснованными (например, о прямолинейности движения). ) Комментарий экспертам:задача проста для олимпиадной, поэтому любые предположения, напрямую не следующие из условия задачи, должны считаться не обоснованными (например, о прямолинейности движения). |
| Образец возможного решения задачи №2 | |
1. 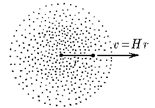 Рассмотрим движение пылинки массой Рассмотрим движение пылинки массой 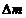 , находящегося на расстоянии , находящегося на расстоянии 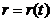 от центра при расширении облака. По 2-ому закону Ньютона: от центра при расширении облака. По 2-ому закону Ньютона: 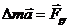 , (1) где ускорение пылинки (м.т.) , (1) где ускорение пылинки (м.т.) 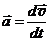 . По закону всемирного тяготения: . По закону всемирного тяготения: 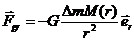 . (2) 2. Предполагая движение радиальным, запишем для массы . (2) 2. Предполагая движение радиальным, запишем для массы 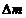 2-ой закон Ньютона в проекции на радиальное направление 2-ой закон Ньютона в проекции на радиальное направление 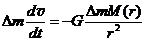 (3) 3. Заметив, что при радиальном движении скорость точек среды (3) 3. Заметив, что при радиальном движении скорость точек среды 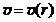 , а масса шара радиусом , а масса шара радиусом 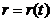 остается постоянной остается постоянной 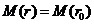 , где , где 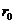 – радиальная координата пылинки в начальный момент времени. Используя правило вычисления производной сложной функции, получим: – радиальная координата пылинки в начальный момент времени. Используя правило вычисления производной сложной функции, получим: 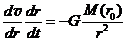 . (4) Учитывая, что . (4) Учитывая, что 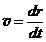 , проинтегрируем уравнение (4): , проинтегрируем уравнение (4): 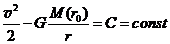 . (5) 4. Облако пыли будет неограниченно расширятся, если . (5) 4. Облако пыли будет неограниченно расширятся, если 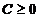 . В начальный момент времени: . В начальный момент времени: 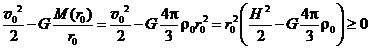 . (6) Из уравнения (6) делаем вывод о том, облако будет неограниченно расширяться при наибольшей начальной плотности . (6) Из уравнения (6) делаем вывод о том, облако будет неограниченно расширяться при наибольшей начальной плотности 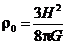 . Ответ: . Ответ: 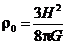 . . | |
| Критерии оценки выполнения задания | Баллы |
Приведено полное правильное решение, включающее следующие элементы: I) записаны положения теории и физические законы, закономерности; применение которых необходимо для решения задачи выбранным способом (в данном случае: 2-ой закон Ньютона, сила тяготения, действующая на пылинку - п.1); II) описаны все вновь вводимые в решении буквенные обозначения физических величин (за исключением обозначений констант, и обозначений, используемых в условии задачи) п. 1-2; III) проведены необходимые математические преобразования и расчёты, приводящие к правильному ответу (п.3-4 формулы(4-6)), IV) представлен правильный ответ (в данном случае – 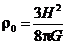 ,) Комментарий экспертам:задача имеет простое решение в виде уравнения Бернулли для идеальной жидкости с нулевым давлением, но в этом случае д.б. приведен его вывод. ,) Комментарий экспертам:задача имеет простое решение в виде уравнения Бернулли для идеальной жидкости с нулевым давлением, но в этом случае д.б. приведен его вывод. |
| Образец возможного решения задачи №3 | |
1. 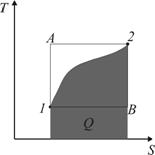 Проще всего данную задачу решать использую Проще всего данную задачу решать использую 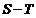 диаграмму процесса. В соответствии с условием задачи, количество теплоты, которое может быть передано в процессе 1–2: диаграмму процесса. В соответствии с условием задачи, количество теплоты, которое может быть передано в процессе 1–2: 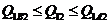 , 2. Следовательно минимальное количество теплоты при переходе вещества из состояния 1 в состояние 2 может быть передано в процессе 1–B–2 и равно , 2. Следовательно минимальное количество теплоты при переходе вещества из состояния 1 в состояние 2 может быть передано в процессе 1–B–2 и равно 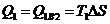 , (2) а максимальное количество теплоты при переходе вещества из состояния 1 в состояние 2 может быть передано в процессе 1–A–2 и равно , (2) а максимальное количество теплоты при переходе вещества из состояния 1 в состояние 2 может быть передано в процессе 1–A–2 и равно 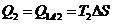 . (3) где . (3) где 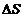 – приращение энтропии. Из (2) и (3) получим – приращение энтропии. Из (2) и (3) получим 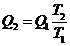 Ответ: Ответ: 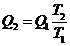 . . | |
| Критерии оценки выполнения задания | Баллы |
Приведено полное правильное решение, включающее следующие элементы: I) записаны положения теории и физические законы, закономерности; применение которых необходимо для решения задачи выбранным способом (в данном случае: графически показано, что количество теплоты при переходе вещества из состояния 1 в состояние 2 ограничено сверху и снизу, графически найдено количество теплоты - п.1-2); II) описаны все вновь вводимые в решении буквенные обозначения физических величин (за исключением обозначений констант, и обозначений, используемых в условии задачи) п. 1-2; III) проведены необходимые математические преобразования и расчёты, приводящие к правильному ответу, IV) представлен правильный ответ (в данном случае – 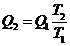 ,) Комментарий экспертам:задача может быть решена с использованием теоремы Карно. Упрощением задачи следует считать применение модели идеального газа к данному веществу. ,) Комментарий экспертам:задача может быть решена с использованием теоремы Карно. Упрощением задачи следует считать применение модели идеального газа к данному веществу. |
| Образец возможного решения задачи №4 | |
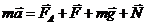 , (1) , (1) 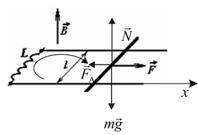 В проекции на ось В проекции на ось 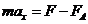 , (2) где сила Ампера: , (2) где сила Ампера: 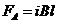 , (3) , (3) 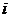 – сила тока в проводниках, положительное направление которого показано на рис. – сила тока в проводниках, положительное направление которого показано на рис.
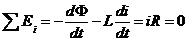 , (4) т.к. по условию задачи можно пренебречь сопротивлением проводников. , (4) т.к. по условию задачи можно пренебречь сопротивлением проводников.
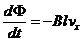 . (5) . (5)
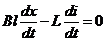 (6) Интегрируя (6), получим (6) Интегрируя (6), получим 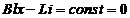 (из начальных условий) (6) (из начальных условий) (6)
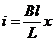 и силу Ампера и силу Ампера 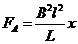 , (7) , (7)
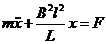 (8) или (8) или 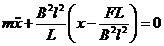 – это диф. ур-ние гармонических колебаний. – это диф. ур-ние гармонических колебаний.
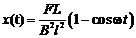 , где циклическая частота , где циклическая частота 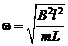 Ответ: Ответ: 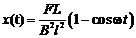 , где циклическая частота , где циклическая частота 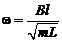 . . | |
| Критерии оценки выполнения задания | Баллы |
Приведено полное правильное решение, включающее следующие элементы: I) записаны положения теории и физические законы, закономерности; применение которых необходимо для решения задачи выбранным способом (в данном случае: 2-ой закон Ньютона, сила Ампера, явление электромагнитной индукции (ЭМИ) и самоиндукции - пп.1–5); II) описаны все вновь вводимые в решении буквенные обозначения физических величин (за исключением обозначений констант, и обозначений, используемых в условии задачи) пп. 1-5; III) проведены необходимые математические преобразования и расчёты, приводящие к правильному ответу пп.6–7, IV) представлен правильный ответ (в данном случае – 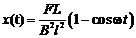 , где циклическая частота , где циклическая частота 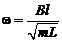 .,) .,) |
| Образец возможного решения задачи №5 | |
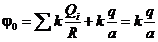 , (1) так как , (1) так как 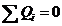 . . 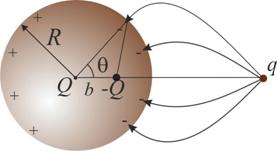 В соответствии с методом изображений разместим заряды: В соответствии с методом изображений разместим заряды: 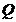 в центре, а в центре, а 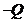 на расстоянии на расстоянии 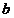 от центра. Тогда потенциал на поверхности сферы от центра. Тогда потенциал на поверхности сферы 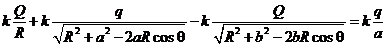 , (2) , (2)
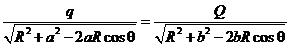 , (3) После не сложных алгебраических преобразований, получим , (3) После не сложных алгебраических преобразований, получим 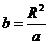 . (4) . (4) 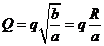 . (5) . (5)
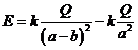 (6) и направлена к центру шара. (6) и направлена к центру шара.
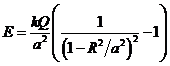 (7) Следовательно, сила, действующая на точечный заряд (7) Следовательно, сила, действующая на точечный заряд 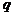 , равна , равна 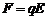 и с учетом (7) и 3-его закона Ньютона и с учетом (7) и 3-его закона Ньютона 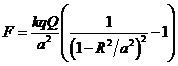 Ответ: Ответ: 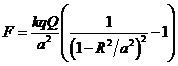 ,. ,. | |
| Критерии оценки выполнения задания | Баллы |
Приведено полное правильное решение, включающее следующие элементы: I) записаны положения теории и физические законы, закономерности; применение которых необходимо для решения задачи выбранным способом (в данном случае: 3-ий закон Ньютона, принцип суперпозиции электрических полей, метод изображений, - пп.1,3,4); II) описаны все вновь вводимые в решении буквенные обозначения физических величин (за исключением обозначений констант, и обозначений, используемых в условии задачи) пп. 1-4; III) проведены необходимые математические преобразования и расчёты, приводящие к правильному ответу пп.2–4, IV) представлен правильный ответ (в данном случае – 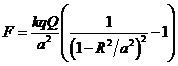 .) .) |
ДЕМОВЕРСИЯ ВАРИАНТОВ ВСО
ВСО-13
- Вертикально расположенный диск радиуса r катится без проскальзывания по горизонтальной поверхности. Три точки А, В и С отмечены на ободе диска таким образом, что дуги АВ и ВС равны a (0<a<p/2). Найти величину угловой скорости диска в тот момент, когда сумма расстояний точек А, В и С до горизонтальной поверхности минимальна, считая скорость точки А в этот момент известной и равной v.
- Ракета массы m0 = 1 т с поперечным сечением S = 5 м2 летела с выключенным двигателем и попала в облако пыли. Масса каждой пылинки m1 = 10-6 кг, их концентрация n =10-4 м-3, а соударения с ракетой абсолютно неупругие. Какова длина облака l, если после пролета через него ракета потеряла 1% скорости?
- Между двумя плоскостями с постоянными температурами T1 и T2 (T1 > T2) находится идеальный газ с молярной массой M. Расстояние между плоскостями равно H. К верхней плоскости на невесомой пружине подвешен маленький шарик массой m, средняя плотность которого равна r0. Длина пружины в недеформированном состоянии L0. Коэффициент жёсткости пружины равен k. Температура линейно возрастает при удалении от нижней плоскости. Найдите давление в газе p, если в положении равновесия длина пружины равна её длине в недеформированном состоянии L0 .
- Три одинаковых изолированных металлических шара расположены в вершинах равностороннего треугольника. Проволочкой, подключенной к удаленному заряженному проводнику, потенциал которого неизвестен, но поддерживается постоянным, по очереди касаются каждого из шаров. Заряды на первых двух шарах оказались после этого равными q1и q2. Найти заряд q3 на третьем шаре.
- Определить энергию кулоновского расталкивания протонов в ядре с массовым числом A в предположении, что протоны распределены по ядру равномерно. Число протонов в ядре Z. Указание: радиус ядра
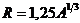 10-15 м.
10-15 м.
Решение задач
Задача №1
Определим положение точек А,В и С в заданный момент времени. Для этого мысленно поместим в эти точки одинаковые массы. Тогда сумма расстояний от точек А,В и С до поверхности пропорциональна потенциальной энергии системы трех точечных масс. Очевидно, минимум потенциальной энергии достигается, когда центр масс системы занимает наинизшее положение, что происходит, когда точка В касается поверхности.
Так, как скорость точки А равна v, длина отрезка ВА равна 2rsin(α/2),а точка В является мгновенным центром скоростей, величина угловой скорости диска 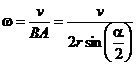
Ответ: 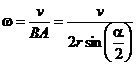
Задача №2

Задача №3

Задача № 4
Указание. Решение. Потенциалы проводников являются линейными однородными функциями их зарядов: 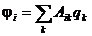 В силу симметрии все коэффициенты Aik с одинаковыми индексами равны
В силу симметрии все коэффициенты Aik с одинаковыми индексами равны
между собой. Точно так же равны все коэффициенты с разными индексами. Обозначая эти коэффициенты через А и В соответственно, можем написать j1=Aq1+ B(q2 + q3) и аналогично для остальных проводников. При зарядке первого шара он получает потенциал j1=Aq1. При зарядке остальных двух шаров потенциал первого шара меняется, но его значения для решения не нужны. При зарядке второго шара его потенциал становится равным такжеj1 = Aq2 + Bq1. Аналогично, для третьего шара j1 = Aq3 + B(q1 + q2). Таким образом, Aq1 = Aq2 + Bq1 = Aq3 + B(q1 + + q2).
Ответ: 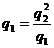
Решение задачи №5
Энергия кулоновского взаимодействия определяется так:
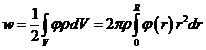 .
.
Плотность зарядов в шаре определим так:
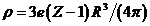 ,
,
Тогда при 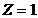 энергия взаимодействия равна нулю.
энергия взаимодействия равна нулю.
Напряжённость электрического поля равномерно заряженного шара зависит от расстояния r до его центра:
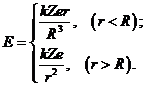
Интегрируя данное соотношение по радиусу от r 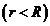 до бесконечности, находим потенциал
до бесконечности, находим потенциал
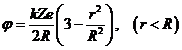 .
.
Подставляя потенциал в верхнюю формулу и интегрируя, получаем
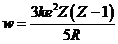 .
.
Наконец, подставляя радиус ядра и элементарный заряд, получаем
Ответ: 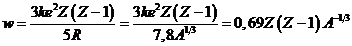 , эрг
, эрг
ВСО-14
1. Верхний конец однородного стержня массой M и длиной L шарнирно закреплён. Маленький шарик массой m подвешен на нити длиной L в точке крепления стержня. От вертикально расположенного и находящегося в покое стержня шарик отводят в сторону так, что он поднимается на высоту h относительно нижнего положения, и отпускают. На какую высоту поднимутся шарик и конец стержня после неупругого удара? Как изменится ответ, если отклонить и отпустить с той же высоты конец стержня, а не шарик?
2. Волк преследует зайца, который удирает от него к норе с постоянной скоростью u . Скорость волка 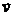 постоянна по величине направлена все время на зайца, причем v>u, В начальный момент
постоянна по величине направлена все время на зайца, причем v>u, В начальный момент 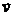 ^
^  , расстояние между волком и зайцем равно L, а расстояние от зайца до норы равно b . Найти время погони t и наибольшее начальное расстояние Lмакс., при котором волк догонит зайца.
, расстояние между волком и зайцем равно L, а расстояние от зайца до норы равно b . Найти время погони t и наибольшее начальное расстояние Lмакс., при котором волк догонит зайца.
3.  Боковые стенки цилиндра АС и BD, его крышка СD и поршень MN сделаны из материала, не проводящего тепло. Поршень MN может двигаться в цилиндре без трения. Сверху и снизу поршня находится по одному молю одного и того же идеального газа с молярной теплоемкостью при постоянном объеме
Боковые стенки цилиндра АС и BD, его крышка СD и поршень MN сделаны из материала, не проводящего тепло. Поршень MN может двигаться в цилиндре без трения. Сверху и снизу поршня находится по одному молю одного и того же идеального газа с молярной теплоемкостью при постоянном объеме 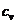 и показателем адиабаты
и показателем адиабаты 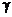 . Первый газ в нижней части цилиндра квазистатически нагревают, вследствие чего поршень MN перемещается. Выразить теплоемкость первого газа С1 при таком процессе через объемы газов V1 в верхней части и V2 в нижней части. Чему равна теплоемкость второго газа?
. Первый газ в нижней части цилиндра квазистатически нагревают, вследствие чего поршень MN перемещается. Выразить теплоемкость первого газа С1 при таком процессе через объемы газов V1 в верхней части и V2 в нижней части. Чему равна теплоемкость второго газа?
4. Образец радия 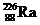 массой
массой 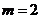 г находится в свинцовой оболочке, не проницаемой для
г находится в свинцовой оболочке, не проницаемой для 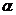 -частиц. Период полураспада радия равен
-частиц. Период полураспада радия равен 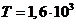 лет, а масса и средняя скорость
лет, а масса и средняя скорость 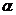 -частиц равны
-частиц равны 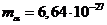 кг и
кг и 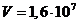 м/с, соответственно. Учитывая отдачу, получаемую ядрами при распаде, найти количество теплоты Q, которое выделится в образце и оболочке за время
м/с, соответственно. Учитывая отдачу, получаемую ядрами при распаде, найти количество теплоты Q, которое выделится в образце и оболочке за время 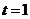 мин?
мин?
5. Однородная немагнитная сплошная среда содержит случайно распределенные включения в виде небольших одинаковых стальных шариков радиуса r с постоянной магнитной проницаемостью μ. Средняя концентрация шариков равна n. Расстояние между шариками намного больше их размеров, так, что влиянием шариков друг на друга можно пренебречь. Найдите среднюю по объему магнитную проницаемость среды.
РЕШЕНИЕ
Волк преследует зайца, который удирает от него к норе с постоянной скоростью u . Скорость волка 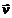 постоянна по величине и направлена все время на зайца, причем v>u, В начальный момент
постоянна по величине и направлена все время на зайца, причем v>u, В начальный момент 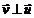 , расстояние между волком и зайцем равно L, а расстояние от зайца до норы равно b. Найти время погони t и наибольшее начальное расстояние Lмакс., при котором волк догонит зайца.
, расстояние между волком и зайцем равно L, а расстояние от зайца до норы равно b. Найти время погони t и наибольшее начальное расстояние Lмакс., при котором волк догонит зайца.

Рис.2. Пояснение к решению задачи №2.
Обозначим расстояние между участниками погони в произвольный момент времени через l (рис 2). За последующий бесконечно малый интервал времени dt волк сместится на расстояние vdt, заяц – на расстояние udt, а расстояние между нимистанет равным l + dl (рис.3). Стороны треугольника, изображенного на рисунке, связаны теоремой косинусов:
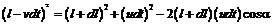
Раскрывая скобки пренебрегая слагаемыми второго порядка малости, находим:
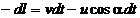
Интегрируя это уравнение с учетом начальных условий, получим:
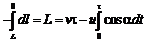 , (1)
, (1)
где в момент времени t = t происходит встреча и l = 0. С другой стороны, в момент встречи координаты участников должны быть одинаковыми, т.е.
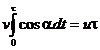 . (2)
. (2)
Исключив 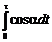 из уравнений (1) и (2), находим время погони t и координату точки встречи:
из уравнений (1) и (2), находим время погони t и координату точки встречи:
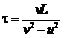 и
и 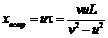
Так, как встреча состоится только если xвстр < b, то максимальное начальное расстояние между волком и зайцем, при котором охота будет успешной, равно:
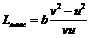

Рис.3. Перемещения волка и зайца за малый промежуток времени.
Образец возможного решения задачи №2
Верхний конец однородного стержня массой M и длиной L шарнирно закреплён. Маленький шарик массой m подвешен на нити длиной L в точке крепления стержня. От вертикально расположенного и находящегося в покое стержня шарик отводят в сторону так, что он поднимается на высоту h относительно нижнего положения, и отпускают. На какую высоту поднимутся шарик и конец стержня после неупругого удара? Как изменится ответ, если отклонить и отпустить с той же высоты конец стержня, а не шарик?
Для решения задачи нужно проанализировать следующие этапы движений:
Опускание шарика, столкновение его со стержнем, последующий подъем шарика и отклонение стержня. На первом и третьем этапах сохраняется механическая энергия. Зато на втором этапе сохраняется момент импульса системы из-за кратковременности удара.
Применяя закон сохранения энергии для первого этапа
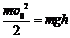
получим скорость шарика 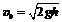 , с которой он ударяется о конец стержня. Далее приравниваем момент импульса шарика со стержнем до столкновения и после:
, с которой он ударяется о конец стержня. Далее приравниваем момент импульса шарика со стержнем до столкновения и после:
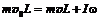 , (3)
, (3)
где w - угловая скорость, которую приобрел стержень в результате неупругого удара, 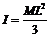 – момент инерции стержня относительно точки подвеса,
– момент инерции стержня относительно точки подвеса, 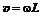 – скорость конца стержня и шарика непосредственно после удара. Выразим эту скорость из (3):
– скорость конца стержня и шарика непосредственно после удара. Выразим эту скорость из (3):
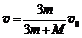 . (2)
. (2)
Будет ли на следующем этапе движения шарик отставать от конца стержня? Для ответа на этот вопрос найдем, на какую высоту поднялись бы шарик и конец стержня, если бы они не взаимодействовали на этом этапе движения. Для шарика закон сохранения энергии дает высоту подъема

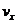
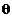 при условии:
при условии: