Работа при вращательном движении тела

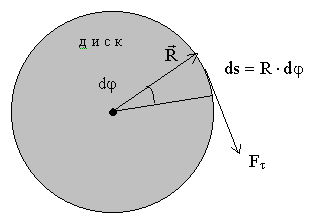
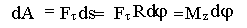
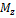- момент силы 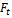относительно оси вращения z.

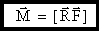- векторное произведение.

Кинетическая энергия и ее связь с работой внешних сил. Кинетическая энергия вращающегося твердого тела.

Связь кинетической энергии с работой.

Если постоянная сила действует на тело, то оно будет двигаться в направлении силы. Тогда элементарная работа по перемещению тела из точки 1 в точку 2, будет равна произведению силы F на перемещение dr :

dA = F dr, отсюда ,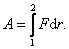
,

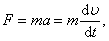
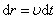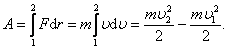
Окончательно получаем:

.

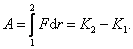Следовательно, работа силы, приложенной к телу на пути r, численно равна изменению кинетической энергии этого тела:

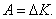(5.1.4)

Или изменение кинетической энергии dK равно работе внешних сил:

dK = dA.

Кинетическая энергия при вращательном движении

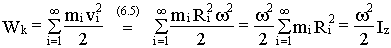
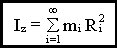
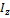- момент инерции твердого тела, относительно оси z.

Моментом инерции материальной точки 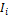называется величина:

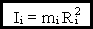
Следовательно,

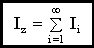
Величина I зависит от положения оси вращения и от распределения масс в теле.

Консервативные силы. Потенциальная энергия. Связь потенциальной энергии и консервативной силы.

Сила, приложенная к материальной точке, называется консервативной, если ее работа зависит только от начального и конечного положения точки.

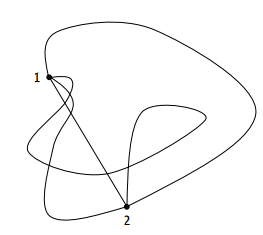
Это значит, что при перемещении материальной точки изположения 1 в положение 2 вдоль любой траектории работа будет одна и та же.

Потенциальной энергией материальной точки, на которую действует консервативная сила, называется работа этой силы при перемещении точки из данного положения в нулевое: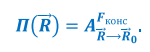

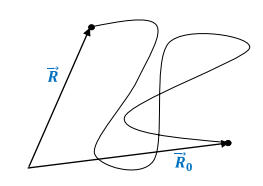
Очевидно, понятие потенциальной энергии может быть введено, только в случае действия консервативной силы.

Нулевое положение выбирается произвольно, за некоторыми исключениями, о которых будет оговорено отдельно. Таким образом, потенциальная величина относительна, как и множество величин в физике.

Конфигурацией системы называется совокупность положений всех тел, входящих в эту систему.

Потенциальной энергией системы тел, на которые действуют консервативные силы, называется работа этих сил при переходе системы из данной конфигурации в нулевую.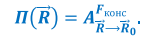

Теорема о потенциальной энергии

Работа консервативных сил, приложенных к системе, равна убыли ее потенциальной энергии: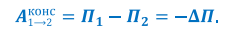

Доказательство (Для материальной точки)

Пусть 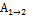— работа консервативной силы при перемещении тела из точки 1 в точку 2. Поскольку сила консервативна, форма траектории (если она проведена между указанными точками) значения не имеет, стало быть, мы можем провести ее через нулевое положение. Тогда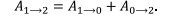

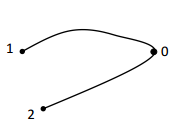Но, согласно определению потенциальной энергии 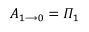— потенциальная энергия тела в положении 1. Аналогично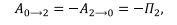

где — потенциальная энергия тела в положении 2. Стало быть,

что и требовалось доказать.