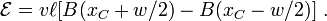Запишите закон Ома в дифференциальной форме и поясните все величины.

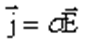дифференциальная форма закона Ома.

где:

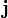• — вектор плотноститока,
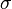• — удельнаяпроводимость,
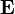• — вектор напряжённостиэлектрическогополя.

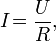интегральная форма

Вычислим Rчерез 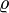— удельное сопротивление материала: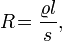

I=U/R=US/l 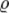следуетчтоU= Il 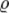/S

E=U/l=Il 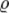/Sl=(I/S )* 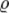следуетI/S=E/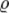

1/ 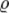= следует что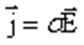

9 вопрос

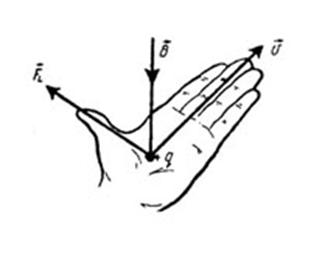
При движении частицы в магнитном поле сила Лоренца не совершает работу , так как она всегда перпендикулярна скорости . отсюда следует что угол равен 90 градусов и значит cosравен 0

A=FScos £=0 ( A=qVBsinβ*cos£) (A=F*r- скалярное произведение)

10 вопрос

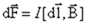
dF_A= IdlBsin £

Два прямых противоположно направленных тока будут отталкиваться друг от друга

Предположим , что они оба бесконечной длины

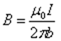
dF₂₁= -I₁dl (µ₀I₂ /2pir)

dF₁₂=I₂dl (-µ₀I₁/ 2 pi r)

dF₂₁=dF₁₂

Сила взаимодействия двух проводников с токами :

F= µ₀I₁I₂dl / 2 pir = µ₀I₁I₂/ 2 pir ( одинаковая длина проводника)

µ₀- магнитная постоянная; I₁I₂– силы токов ; r – расстояние между проводниками

17.

Закон Фарадея [править]

Согласно закону электромагнитной индукции Фарадея (в СИ):

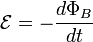
где

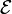— электродвижущая сила, действующая вдоль произвольно выбранного контура,

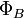
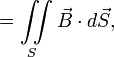— магнитный поток через поверхность, натянутую на этот контур.

Знак «минус» в формуле отражает правило Ленца, названное так по имени русского физика Э. Х. Ленца:

Индукционный ток, возникающий в замкнутом проводящем контуре, имеет такое направление, что создаваемое им магнитное поле противодействует тому изменению магнитного потока, которым был вызван данный ток.

Для катушки, находящейся в переменном магнитном поле, закон Фарадея можно записать следующим образом:

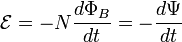
где

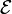— электродвижущая сила,

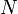— число витков,

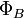— магнитный поток через один виток,

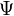— потокосцепление катушки.

Следует отметить, что закон Фарадея в такой форме, очевидно, описывает лишь ту часть ЭДС, что возникает при изменении магнитного потока через контур за счёт изменения со временем самого поля без изменения (движения) границ контура (об учете последнего см. ниже).

· В этом виде закон Фарадея входит в систему уравнений Максвелла для электромагнитного поля (в дифференциальной или интегральной форме соответственно)^[1].

Если же, скажем, магнитное поле постоянно, а магнитный поток изменяется вследствие движения границ контура (например, при увеличении его площади), то возникающая ЭДС порождается силами, удерживающими заряды на контуре (в проводнике) и силой Лоренца, порождаемой прямым действием магнитного поля на движущиеся (с контуром) заряды. При этом равенство 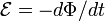продолжает соблюдаться, но ЭДС в левой части теперь не сводится к 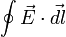(которое в данном частном примере вообще равно нулю). В общем случае (когда и магнитное поле меняется со временем, и контур движется или меняет форму) последняя формула верна так же, но ЭДС в левой части в таком случае есть сумма обоих слагаемых, упомянутых выше (то есть порождается частично вихревым электрическим полем, а частично силой Лоренца и силой реакции движущегося проводника).

16.

Индукцио́нный ток — электрический ток, возникающий в замкнутом проводящем контуре при изменении потока магнитной индукции, пронизывающего этот контур. Величина и направление индукционного тока определяются законом электромагнитной индукции и правилом Ленца.

Магни́тный пото́к — поток 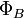как интеграл вектора магнитной индукции 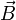через конечную поверхность 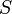. Определяется через интеграл по поверхности

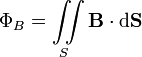
при этом векторный элемент площади поверхности определяется как

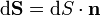
где 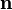— единичный вектор, нормальный к поверхности.

Также магнитный поток можно рассчитать как скалярное произведение вектора магнитной индукции на вектор площади:

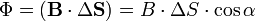
где α — угол между вектором магнитной индукции и нормалью к плоскости площади.

Магнитный поток через контур также можно выразить через циркуляцию векторного потенциала магнитного поля по этому контуру:

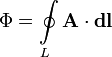
Поток через поверхность и ЭДС в контуре [править]

Определение поверхностного интеграла предполагает, что поверхность Σ поделена на мелкие элементы. Каждый элемент связан с вектором dA, величина которого равна площади элемента, а направление — по нормали к элементу во внешнюю сторону.

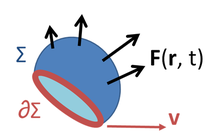
Векторное поле F(r, t) определено во всём пространстве, а поверхность Σ ограничена кривой ∂Σ, движущейся со скоростью v. По этой поверхности производится интегрирование поля.

Закон электромагнитной индукции Фарадея использует понятие магнитного потока Φ_B через замкнутую поверхность Σ, который определён через поверхностный интеграл:

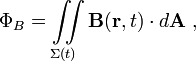
где dA — площадь элемента поверхности Σ(t), B — магнитное поле, а B·dA — скалярное произведение B и dA. Предполагается, что поверхность имеет «устье», очерчённое замкнутой кривой, обозначенной ∂Σ(t). Закон индукции Фарадея утверждает, что когда поток изменяется, то при перемещении единичного положительного пробного заряда по замкнутой кривой ∂Σ совершается работа 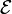, величина которой определяется по формуле:

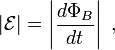
где 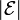— величина электродвижущей силы (ЭДС) в вольтах, а Φ_B — магнитный поток в веберах. Направление электродвижущей силы определяется законом Ленца.

Для плотно намотанной катушки индуктивности, содержащей N витков, каждый с одинаковым магнитным потоком Φ_B, закон индукции Фарадея утверждает, что:

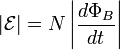
где N — число витков провода, Φ_B — магнитный поток в веберах на один виток.

Закон Ленца [править]

Заряд q в проводнике на левой стороне петли испытывает силу Лоренца q v × B k = −q v B(x_C − w / 2) j   (j, k — единичные векторы в направлениях y и z; см. векторное произведение векторов), что вызывает ЭДС (работу на единицу заряда) v ℓ B(x_C− w / 2) по всей длине левой стороны петли. На правой стороне петля аналогичное рассуждение показывает, что ЭДС равнаv ℓ B(x_C + w / 2). Две противоположные друг другу ЭДС толкают положительный заряд по направлению к нижней части петли. В случае, когда поле B возрастает вдоль х, сила на правой стороне будет больше, а ток будет течь по часовой стрелке. Используя правило правой руки, мы получаем, что поле B, создаваемое током, противоположно приложенному полю.^[13]ЭДС, вызывающая ток, должна увеличиваться по направлению против часовой стрелки (в отличие от тока). Складывая ЭДС в направлении против часовой стелки вдоль петли мы находим: