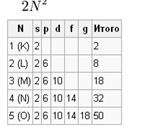
Количество электронов в каждой оболочке

Данное количество вычисляется по формуле:

Правило Хунда определяет порядок заполнения орбиталей определённого подслоя и формулируется следующим образом: суммарное значение спинового квантового числа электронов данного подслоя должно быть максимальным. Сформулировано Фридрихом Хундом в 1925 году.

Это означает, что в каждой из орбиталей подслоя заполняется сначала один электрон, а только после исчерпания незаполненных орбиталей на эту орбиталь добавляется второй электрон. При этом на одной орбитали находятся два электрона с полуцелыми спинами противоположного знака, которые спариваются (образуют двухэлектронное облако) и, в результате, суммарный спин орбитали становится равным нулю.

Другая формулировка: Ниже по энергии лежит тот атомный терм, для которого выполняются два условия. -Мультиплетность максимальна -При совпадении мультиплетностей суммарный орбитальный момент L максимален.

Разберём это правило на примере заполнения орбиталей p-подуровня p-элементов второго периода (то есть от бора до неона (в приведённой ниже схеме горизонтальными чёрточками обозначены орбитали, вертикальными стрелками — электроны, причём направление стрелки обозначает ориентацию спина):

Как видно, сначала появляется один электрон на 2p_x-орбитали, затем один электрон на 2p_y-орбитали, после этого один электрон на 2p_z-орбитали, затем появляются парные электроны на 2p_x-, 2p_y- и 2p_z-орбиталях.

21. Тормозное и характеристическое рентгеновское излучение. Закон Мозли.

Когда энергия бомбардирующих анод электронов становится достаточной для вырывания электронов из внутренних оболочек атома, на фоне тормозного излучения появляются резкие линии характеристического излучения. Частоты этих линий зависят от природы вещества анода, поэтому их и назвали характеристическими.

Состояние атома с вакансией во внутренней оболочке неустойчиво. Электрон одной из внешних оболочек может заполнить эту вакансию, и атом при этом испускает избыток энергии в виде фотона характеристического излучения: 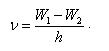Все переходы на k-оболочку образуют K-серию, соответственно, на l- и m-оболочки – L- и M-серии (рис. 2.8).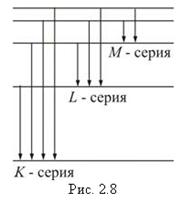

Английский физик Генри Мозли в 1913 году установил закон, названный его именем, связывающий частоты линий рентгеновского спектра с атомным номером испускающего их элемента Z:

Здесь 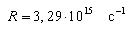, постоянная Ридберга; σ – постоянная, учитывающая экранирующую роль окружающих ядро электронов. Чем дальше электрон от ядра, тем σ больше.

На рис. 2.9 показана графическая зависимость закона.

Закон Мозли позволил по измерению длин волн λ рентгеновских лучей точно установить атомный номер элемента. Он сыграл большую роль при размещение элементов в таблице Менделеева.

22. Физические особенности в молекулярных спектрах. Энергия и спектр двухатомной молекулы. P-, Q- и R-ветви.

Молекула — частица, образованная двумя или большим количеством атомов, характеризующаяся определённым количеством входящих в неё атомных ядер и электронов, а также определённой структурой.

Энергия свободной молекулы состоит из энергии поступательного движения молекулы как единого целого, энергии колебания атомов внутри молекулы, энергии вращения целой молекулы и ее частей относительно друг друга, энергии электронного возбуждения молекулы (энергия движения электронов в молекуле) и внутриядерной энергии:

Е=Епост +Евр+Екол +Еэл +Еяд.

Молекулярные спектры - спектры испускания и поглощения электромагнитного излучения и комбинацию рассеяния света, принадлежащие свободным или слабо связанным молекулам. Имеют вид совокупности полос (линий) в рентгеновской, УФ - видимой, ИК и радиоволновой областях спектра. Положение полос (линий) в спектрах испускания и поглощения характеризуется частотами v и волновыми числами υ; оно определяется разностью энергий Е' и Е: тех состояний молекулы, между которыми происходит квантовый переход:

23. Одномерный кристалл Кронига-Пенни. Понятие о зонной теории твердых тел. Фермионы и бозоны.

КРОНИГА - ПЕННИ МОДЕЛЬ - одномерная, точно решаемая модель движения электронов в периодич. поле, иллюстрирующая природу возникновения энергетич. зон в кристалле (см. Зонная теория). Предложена Р. Кронигом (R. Kronig) и У. Дж. Пенни (W.G. Penney) в 1931. В К--П. м. потенциал V(x), создаваемый кристаллич. решёткой, аппроксимируется периодич. последовательностью прямоугольных потенц. ям глубиной V₀ и шириной а, разделённых потенц. барьерами шириной Ь, так что постоянная решётки равна а+Ь (рис. 1). Решение ур-ния Шрёдингера с потенциалом V(x)имеет вид плоской волны, модулированной с периодом решётки:

В основе зонной теории лежит так называемое адиабатическое приближение. Кван-тово-механическая система разделяется на тяжелые и легкие частицы - ядра и электроны. Поскольку массы и скорости этих частиц значительно различаются, можно считать, что движение электронов происходит в поле неподвижных ядер, а медленно движущиеся ядра находятся в усредненном поле всех электронов. Принимая, что ядра в узлах кристаллической решетки неподвижны, движение электрона рассматривается в постоянном периодическом поле ядер.

Далее используется приближение самосогласованного поля. Взаимодействие данного электрона со всеми другими электронами заменяется действием на него стационарного электрического поля, обладающего периодичностью кристаллической решетки. Это поле создается усредненным в пространстве зарядом всех других электронов и всех ядер. Таким образом, в рамках зонной теории многоэлектронная задача сводится к задаче о движении одного электрона во внешнем периодическом поле - усредненном и согласованном поле всех ядер и электронов.

Фермио́н — частица (или квазичастица) с полуцелым значением спина. Своё название получили в честь физика Энрико Ферми.

Примеры фермионов: кварки (они формируют протоны и нейтроны, которые также являются фермионами), лептоны (электроны, мюоны, тау-лептоны, нейтрино), дырки (квазичастицы в полупроводнике)^[1].

Фермионы подчиняются статистике Ферми — Дирака: в одном квантовом состоянии может находиться не более одной частицы (принцип Паули). Принцип запрета Паули ответственен за стабильность электронных оболочек атомов, делая возможным существование сложных химических элементов. Он также позволяет существовать вырожденной материи под действием высоких давлений (нейтронные звёзды). Волновая функция системы одинаковых фермионов антисимметрична относительно перестановки двух любых фермионов. Квантовая система, состоящая из нечётного числа фермионов, сама является фермионом (например, ядро с нечётным массовым числом A; атом или ион с нечётной суммой A и числа электронов).

Бозо́н (от фамилии физика Бозе) — частица с целым значением спина. Бозоны, в отличие от фермионов, подчиняются статистике Бозе — Эйнштейна, которая допускает, чтобы в одном квантовом состоянии могло находиться неограниченное количество одинаковых частиц. Системы из многих бозонов описываются симметричными относительно перестановок частиц волновыми функциями.

24. Расщепление энергетических уровней и образование зон. Различие между металлами, полупроводниками и диэлектриками в зонной теории.

Несмотря на то, что метод сильной связи применим для электронов глубоких энергетических уровней, он хорошо иллюстрирует общие закономерности образования энергетических зон при сближении изолированных атомов и образования из них кристаллической решетки. Рассмотрим качественно картину возникновения энергетических зон на примере образования кристаллической решетки из изолированных атомов натрия. Электронная структура Na¹¹ (1s²2s²2p⁶3s): всего в атоме 11 электронов, по два электрона на 1s и 2s уровнях, 6 электронов на уровне 2р, последний заполненный уровень в атоме натрия - 3s, на котором находится один валентный электрон. Поскольку в приближении сильной связи предполагается, что состояние электрона в кристалле незначительно отличается от его состояния в изолированном атоме, будем в оценке влияния на это состояние кристаллического поля соседних атомов исходить из энергетической структуры изолированного атома. На рис. 2.1,а показаны схематически энергетические уровни и распределение электронов на них для атомов натрия, находящихся на достаточно большом расстоянии друг от друга так, что потенциальные кривые электронов не перекрываются (взаимодействие между атомами пренебрежимо мало). Состояния электронов в этом случае описываются волновыми функциями изолированного атома, разрешенные уровни энергии дискретны и определяются квантовыми числами n, l, m - главным, орбитальным, магнитным соответственно. На каждом невырожденном по энергии уровне могут находиться с учетом спина по два электрона, а на каждом вырожденном по орбитальному квантовому числу уровне 2(2l +1) электронов.

Различие между металлами и диэлектриками с точки зрения зонной теории состоит в том, что при 0 К в зоне проводимости металлов имеются электроны, а в зоне проводимости диэлектриков они отсутствуют. Различие же между диэлектриками и полупроводниками определяется шириной запрещенных зон: для диэлектриков она довольно широка (например, для NaCl DЕ=6 эВ), для полупроводников — достаточно узка (например, для германия DЕ=0,72 эВ). При температурах, близких к 0 К, полупроводники ведут себя как диэлектрики, так как переброса электронов в зону проводимости не происходит. С повышением температуры у полупроводников растет число электронов, которые вследствие теплового возбуждения переходят в зону проводимости, т. е. электрическая проводимость проводников в этом случае увеличивается.

25. Свойства и характеристика ядер. Нейтрон и протон, их свойства. Энергия связи ядра.

26. Свойства и модель ядерных сил. Капельная модель ядра. Формула Вейцзеккера для энергии связи. Оболочечная модель ядра.

Силы, действующие между нуклонами в ядре и обеспечивающие существование устойчивых ядер, называются ядерными силами. Ядерные силы обладают рядом особых свойств:

1) Эти силы не относятся ни к одному из типов сил, известных в классической физике.

2) Ядерные силы – силы короткодействующие. Расстояние r , на котором действуют ядерные силы, называются радиусом действия ядерных сил ( r = 2*10^-15 м).

3) Они обладают свойством зарядовой независимости.

4) У них имеется свойство насыщения: каждый нуклон взаимодействует только с ограниченным числом ближайших к нему нуклонов, а не со всеми нуклонами ядра.

5) Ядерные силы не являются центральными силами, в отличие от кулоновских и гравитационных сил.

6) Ядерные силы имеют обменный характер. Это проявляется в том, что силы, действующие между двумя ядерными частицами, рассматриваются как результат обмена между ними некоторой промежуточной частицей( Pi⁺ - мезоном) Ядерные силы детально не изучены до сих пор. Законченной теории ядерных сил не существует. Плодотворным методом изучения различных свойств атомного ядра является метод моделей ядра, основанной на внешней аналогии свойств атомных ядер со свойствами других систем, хорошо изученных в физике.

В капельной модели ядро рассматривается как сферическая капля несжимаемой заряженной ядерной жидкости радиуса R = r₀A^1/3. То есть в энергии связи ядра учитываются объемная, поверхностная и кулоновская энергии. Дополнительно учитываются выходящие за рамки чисто капельных представлений энергия симметрии и энергия спаривания. В рамках этой модели можно получить полуэмпирическую формулу Вайцзеккера для энергии связи ядра.

E_св(A,Z) = a₁A - a₂A^2/3 - a₃Z²/A^1/3 - a₄(A/2 - Z)²/A + a₅A^-3/4.

Первое слагаемое в энергии связи ядра, подобного жидкой капле, пропорционально массовому числу A и описывает примерное постоянство удельной энергии связи ядер.
Второе слагаемое - поверхностная энергия ядра уменьшает полную энергию связи, так как нуклоны, находящиеся на поверхности имеют меньше связей, чем частицы внутри ядра. Это аналог поверхностного натяжения.
Третье слагаемое в энергии связи обусловлено кулоновским взаимодействием протонов. В капельной модели предполагается, что электрический заряд протонов равномерно распределен внутри сферы радиуса R = r₀A^1/3.
Четвертое слагаемое - энергия симметрии ядра отражает тенденцию к стабильности ядер с N = Z.
Пятое слагаемое - энергия спаривания учитывает повышенную стабильность основных состояний ядер с четным числом протонов и/или нейтронов.
Входящие в формулу коэффициенты a₁, a₂, a₃, a₄ и a₅ оцениваются из экспериментальных данных по знергиям связи ядер, что дает

Экспериментальные значения удельной энергии связи и расчет по формуле Вейцзеккера

a₁ = 15.75 МэВ; a₂ = 17.8 МэВ; a₃ = 0.71 МэВ; a₄ = 94.8 МэВ;

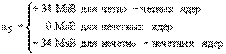
На рисунке показаны экспериментальные значения удельной энергии связи = E_св/A и расчет по формуле Вайцзеккера (плавная кривая).
Формула Вайцзеккера позволяет по заданным значениям A и Z вычислять энергию связи ядра с погрешностью ~10 МэВ. При A 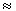100 это дает относительную ошибку ~10^-2. Наибольшее расхождение между эспериментально измеренными величинами энергии связи ядра и расчетами по формуле Вайцзеккера наблюдается в области магических чисел. Это объясняется тем, что в капельной модели не учитываются неоднородности распределения ядерной материи, обусловленные оболочечной структурой атомных ядер.

27. Искусственная и естественная радиоактивность. Основной закон радиоактивного распада. Активность. Правила смещения.