Вынужденные электрические колебания в колебательном контуре. Резонанс, резонансные кривые.

Вернёмся к уравнению вынужденных колебаний (11.14):

U_R + U_C + U_L = U₀coswt.

Теперь мы знаем, что здесь:

U_R = I₀Rcoswt;

;

.

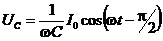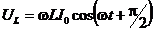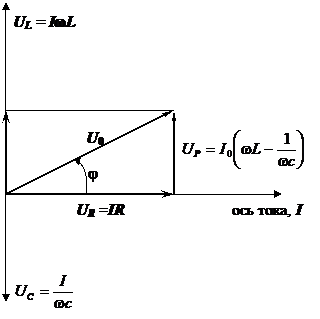Сложим эти три гармонические колебания, воспользовавшись методом векторных диаграмм (рис. 11.10.). Для этого выберем ось тока (I). U_R представим вектором, совпадающим по направлению с направлением оси тока. Напряжения U_C и U_L будут представлены векторами, повёрнутыми относительно оси тока на 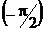и 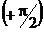соответственно.

Рис. 11.10.

Сложение трёх колебаний заменим теперь сложением этих трёх векторов.

Сумма падений напряжений на индуктивности и ёмкости определит реактивную составляющую полного напряжения — U_р.

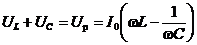. (11.18)

Амплитуда этого напряжения, как следует из (11.18) пропорциональна амплитуде тока.

Рассматривая последнее уравнение, как запись закона Ома, можно коэффициент пропорциональности между током и напряжением назвать сопротивлением этого участка.

R_p= 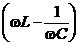— реактивное сопротивление контура.

Продолжим сложение векторов и к уже полученной сумме прибавим вектор, изображающий U_R = I₀R.

Результатом сложения всех трёх колебаний (векторов) будет напряжение U = U₀coswt, поддерживающее вынужденные колебания в контуре (см. 11.4).

Как следует из векторной диаграммы, амплитуда этого напряжения равна:

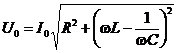. (11.19)

Или амплитуда тока в цепи:

.

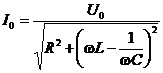При этом ток будет запаздывать по фазе от напряжения на j:

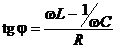. (11.21)

Уравнения (11.19) и (11.20) иногда называют законом Ома для переменного тока. Но надо иметь в виду, что эти формулы связывают только амплитудные значения тока I₀ и напряжения U₀.

В уравнении (11.21) 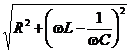— полное сопротивление колебательного контура, складывающееся из активного (R) и реактивного 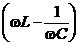сопротивлений.

Теперь проанализируем полученные результаты (11.20) и (11.21).

Пусть в колебательном контуре RLC (рис. 11.6.) действует источник переменного напряжения:

U = U₀coswt.

Теперь мы уже знаем, что в контуре установятся гармонические колебания тока:

I = I₀cos(wt – j).

Амплитуда этого колебания прямо пропорциональна амплитуде приложенного напряжения U₀ и обратно пропорциональна полному сопротивлению контура:

.

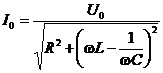Ток будет отставать по фазе от напряжения на угол j:

.

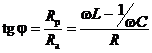Будем теперь менять частоту w возбуждающего сигнала, оставляя его амплитуду U₀ неизменной.

При w = 0, I(w = 0) = 0. Это легко понять: ведь сопротивление колебательного контура, с его ёмкостью С, бесконечно для постоянного тока (R_C = 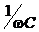= ¥ при w = 0). Отсюда и нулевой ток.

Ток будет стремиться к нулю и в случае неограниченного роста частоты колебаний. При w ® ¥, R_L = wL ® ¥ и I ® 0.

В промежутке между этими предельными значениями частоты, амплитуда тока проходит через максимум. Резонансные кривые для амплитуды силы тока I₀ = I₀(w) приведены на рис. 11.11.

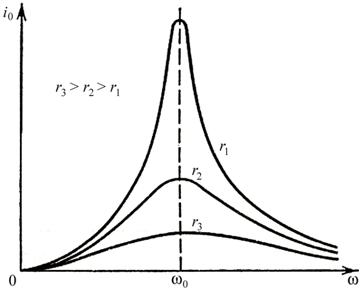
Рис. 11.11.

Амплитуда I₀ достигает максимума, когда реактивное сопротивление контура становится равным нулю:

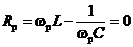. (11.22)

При этой (резонансной) частоте сопротивление контура будет определяться только сопротивлением резистора R:

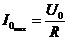(11.23)

Из (11.22) следует, что резонанс тока наступает при частоте w_P = w₀, равной частоте собственных незатухающих колебаний контура:

.

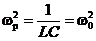Понятно, что уровень резонансного максимума амплитуды тока зависит от величины активного сопротивления контура (11.23).

Анализ зависимости фазового сдвига j от частоты приводит к выводу, который графически представлен на рис 11.12.

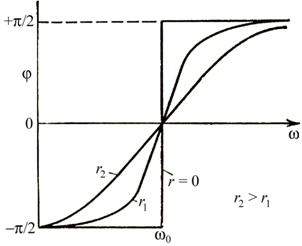
Рис. 11.12.

Наибольший интерес представляет момент резонанса, когда частота вынуждающего сигнала равна частоте w₀. Тогда амплитуда тока достигает своего максимума, а разность фаз между током и приложенным напряжением равна нулю (j = 0).

Контур в этом случае выступает как чисто активное сопротивление.

Этот важный частный случай вынужденных колебаний называется резонансом напряжений. Именно резонанс напряжений используется в радиотехнике при настройке на сигнал строго определённой частоты.